【DFS系列 | 暴力搜索与回溯剪枝】DFS问题实战：如何通过剪枝优化暴力搜索效率

算法	相关知识点	可以通过点击	以下链接进行学习	一起加油！
递归	二叉树中深搜

深度优先搜索（DFS）是解决组合、路径等问题的核心算法，但暴力枚举效率低下。如何通过回溯和剪枝优化DFS，使其更高效？本文通过实战案例，解析DFS从穷举到优化的关键技巧，提升算法效率与性能。

🌈个人主页：是店小二呀
🌈C/C++专栏：C语言\ C++
🌈初/高阶数据结构专栏： 初阶数据结构\ 高阶数据结构
🌈Linux专栏： Linux
🌈算法专栏：算法
🌈Mysql专栏:Mysql

🌈你可知:无人扶我青云志 我自踏雪至山巅

一、回溯算法

1.1 回溯概念

回溯算法是一种经典的递归算法，常用于解决组合、排列和搜索等问题。其基本思想是从初始状态出发，按照一定规则进行前向搜索。当搜索遇到无法继续前进的状态时，回退到上一个状态，再尝试其他可能的路径。回溯算法通过维护一棵状态树来遍历所有可能的解。

回溯算法的核心思想是“试错”。在搜索过程中，我们不断做出选择，若选择正确，则继续前进；若选择错误，则回退到上一个状态并重新选择。回溯算法特别适用于需要寻找多个解，且每个解都需要完整搜索的问题。

1.2 回溯算法的模板

void backtrack(vector<int>& path, vector<int>& choice, ...) {
// 满⾜结束条件
if (/* 满⾜结束条件 */) {
// 将路径添加到结果集中
res.push_back(path);
return;
}
// 遍历所有选择
for (int i = 0; i < choices.size(); i++) {
// 做出选择
path.push_back(choices[i]);
// 做出当前选择后继续搜索
backtrack(path, choices);
// 撤销选择
path.pop_back();
}
}

模板不需要死记硬背，关键在于解决问题的思路。模板只是步骤相似，真正的重点在于理解问题的解决思路。

---

LCR 083. 全排列

【题目】：LCR 083. 全排列

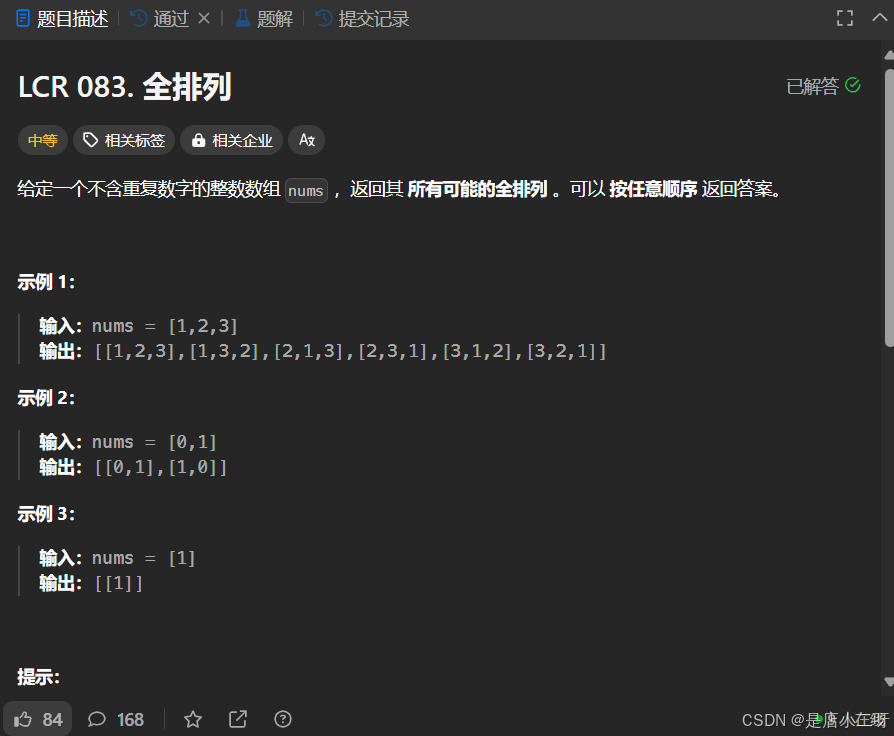
【算法思路】

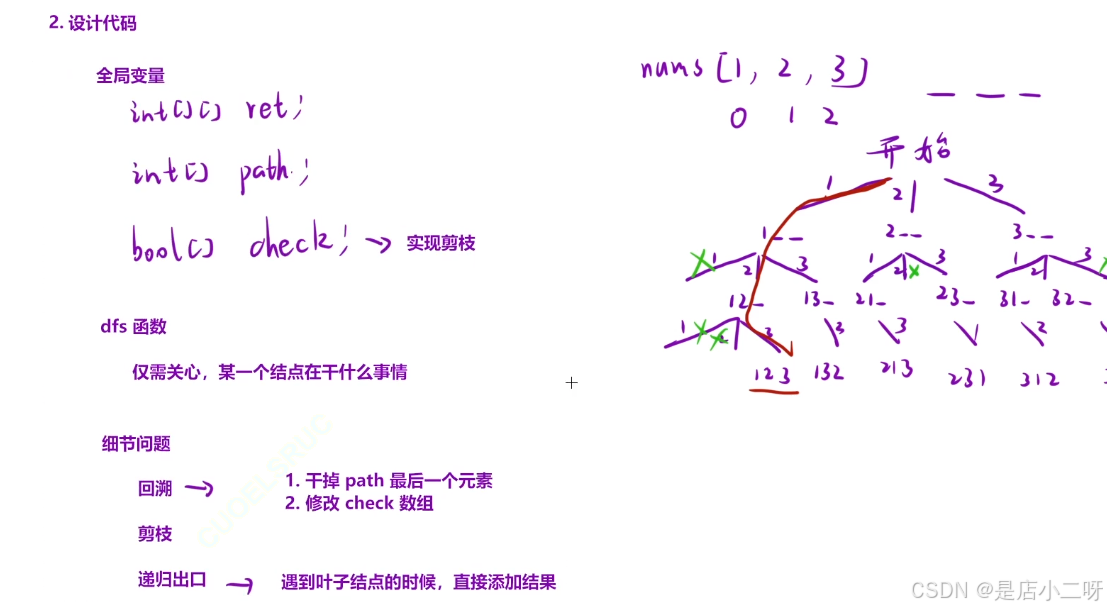
在这里，我们选择将数组元素添加到path数组中，相当于做出决策。为了处理这个问题，我们可以借助决策树的思路。由于需要对nums数组的元素进行选择，而递归本身是线性的，单靠递归无法实现元素选择，因此我们结合for循环进行多方向、多元素的递归，并通过添加剪枝条件来优化搜索过程。

此外，涉及到‘回溯中恢复现场’的操作。我们可以选择在return语句之前恢复现场，或者在之后恢复现场。由于后续还会有循环递归，选择了在递归后恢复现场的方式。注意使用bool数组进行剪枝

【代码实现】

class Solution {
public:vector<vector<int>> ret;vector<int> path;bool check[9];vector<vector<int>> permute(vector<int>& nums) {dfs(nums);return ret;}void dfs(vector<int>& nums){if(path.size() == nums.size()){ret.push_back(path);return ;}for(int i = 0; i < nums.size(); i++){if(check[i] == false){path.push_back(nums[i]);check[i] = true;dfs(nums);path.pop_back();check[i] = false;}}}
};

【个人思考】

对于数组元素有多个选择的情况，可以使用循环和递归相结合来实现枚举策略。当然，也可以根据不同的选择走不同的递归路径，但这需要根据题意来判断。最终，还是要明确这个树的作用。

---

LCR 079. 子集

【题目】：LCR 079. 子集

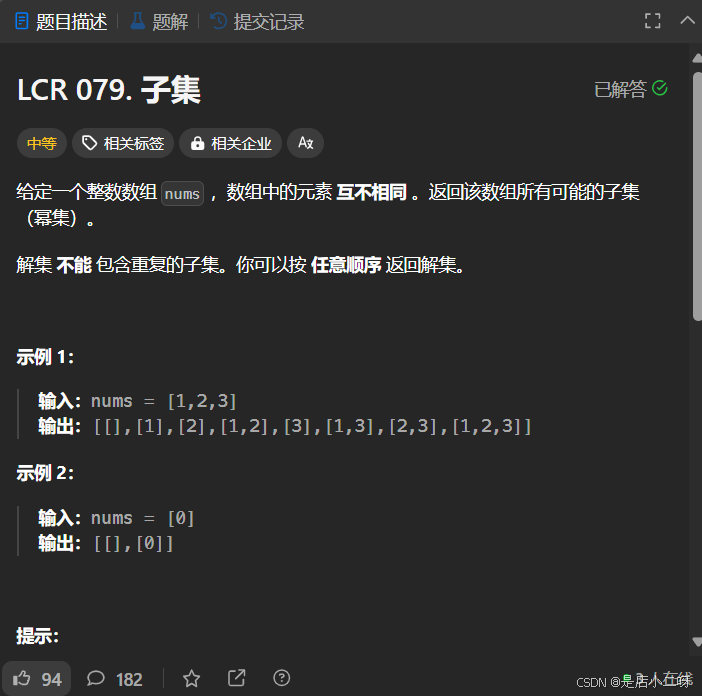
【算法思路】

解法一：

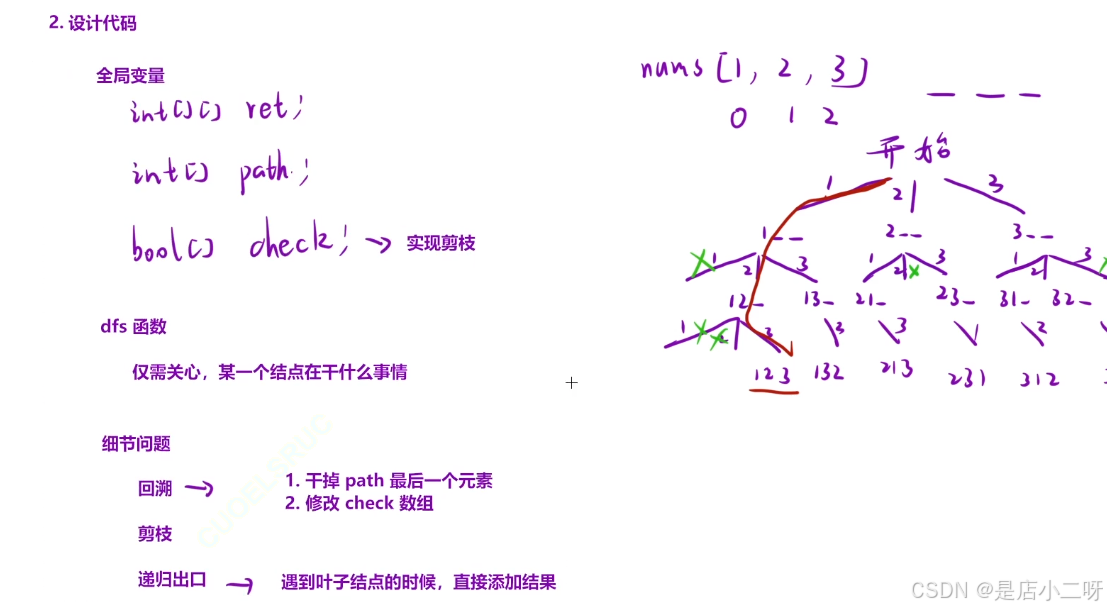
只要我们将决策树绘制出来，剩下的就是编写代码的任务。关键在于如何设计递归函数。通过决策树，我们可以看出需要使用 pos 变量来标记当前的递归步骤。

函数的作用:是查找集合的所有子集，并将它们存储到答案列表中。

在设计函数体时，可以将其视为两条递归路径：选择与不选择。我们通常先处理‘选择’的情况，因为这样可以方便地恢复选择状态，然后再递归地处理‘不选择’的情况。注意，这里要特别关注递归函数体的设计

【代码实现】

class Solution {
public:vector<vector<int>> ret;vector<int> path;vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return ret;}void dfs(vector<int>& nums,int pos){if(pos == nums.size()){ret.push_back( path);return;}//选择这个数据path.push_back(nums[pos]);dfs(nums, pos + 1);path.pop_back();//不选择dfs(nums, pos + 1);}
};

解法二：

这个问题与‘全排序’问题有些相似，都是通过循环为节点提供递归路径 pos, n - 1。通过观察我们采用的是后序遍历，即从最后开始处理。可以看到，循环条件已经有效地帮助我们完成了剪枝操作。

【代码实现】

class Solution {
public:vector<vector<int>> ret;vector<int> path;vector<vector<int>> subsets(vector<int>& nums) {dfs(nums, 0);return ret;}void dfs(vector<int>& nums,int pos){       ret.push_back(path);for(int i = pos; i < nums.size(); i++){path.push_back(nums[i]);dfs(nums, i + 1);path.pop_back();}}
};

快和小二一起踏上精彩的算法之旅！关注我，我们将一起破解算法奥秘，探索更多实用且有趣的知识，开启属于你的编程冒险！