第四十四天:动态规划part11(第九章)
1.最长公共子序列
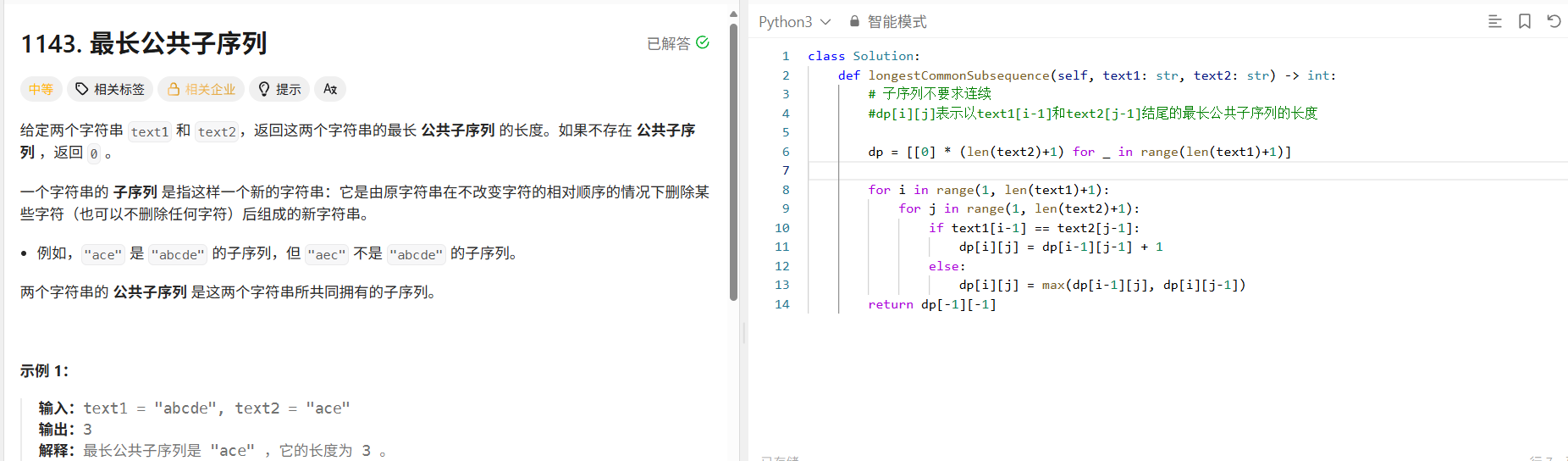
1143. 最长公共子序列 - 力扣(LeetCode)
-
状态转移
-
如果当前字符相等:
dp[i][j]=dp[i−1][j−1]+1dp[i][j] = dp[i-1][j-1] + 1dp[i][j]=dp[i−1][j−1]+1把它们加到前面 LCS 的基础上。
-
如果当前字符不相等:
dp[i][j]=max(dp[i−1][j], dp[i][j−1])dp[i][j] = \max(dp[i-1][j],\ dp[i][j-1])dp[i][j]=max(dp[i−1][j], dp[i][j−1])舍弃
text1当前字符或text2当前字符,取较长结果。
-
-
初始化
-
dp[0][*] = 0和dp[*][0] = 0(一个字符串为空时,公共子序列长度为 0)。
-
-
最终答案
-
dp[len(text1)][len(text2)]。
-
3. 复杂度分析
-
时间复杂度:O(m×n)O(m \times n)O(m×n)
-
空间复杂度:O(m×n)O(m \times n)O(m×n),可优化到 O(min(m,n))O(\min(m, n))O(min(m,n))。
class Solution:def longestCommonSubsequence(self, text1: str, text2: str) -> int:# 子序列不要求连续#dp[i][j]表示以text1[i-1]和text2[j-1]结尾的最长公共子序列的长度dp = [[0] * (len(text2)+1) for _ in range(len(text1)+1)]for i in range(1, len(text1)+1):for j in range(1, len(text2)+1):if text1[i-1] == text2[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])return dp[-1][-1]2.不相交的线
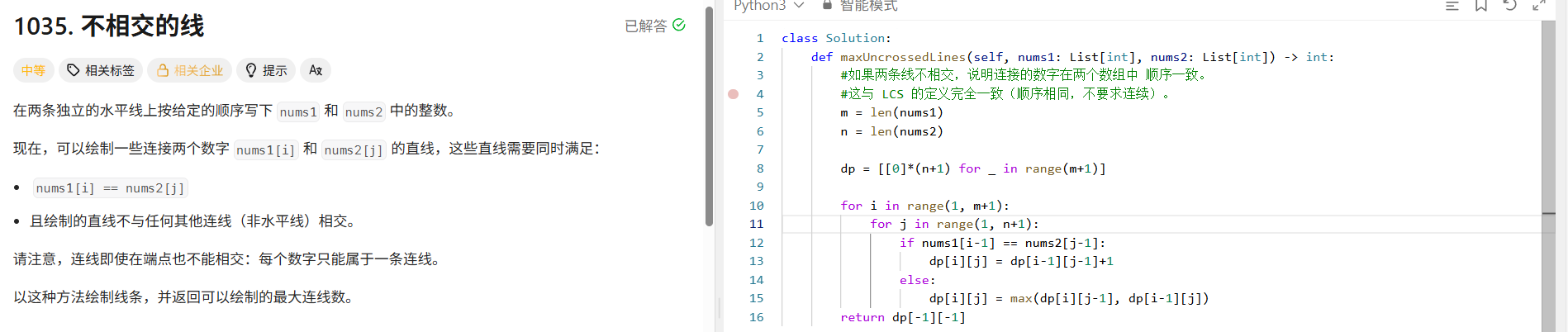
1. 问题本质
-
给定两个数组
nums1和nums2,可以在两个数组中连接相等的数字画线,要求直线不能相交。 -
不相交 的含义是:在两个数组中连接的元素必须保持相对顺序。
-
这和 最长公共子序列(LCS) 问题是完全等价的:
顺序相同,不要求连续。
2. 动态规划思想
状态定义
-
dp[i][j]表示:nums1[0..i-1]和nums2[0..j-1]的最大不相交直线数量。
状态转移
-
如果
nums1[i-1] == nums2[j-1]:-
这两个点可以连一条线,数量 = 之前子问题的数量 + 1
dp[i][j]=dp[i−1][j−1]+1dp[i][j] = dp[i-1][j-1] + 1dp[i][j]=dp[i−1][j−1]+1
-
-
如果不相等:
-
只能舍弃
dp[i][j]=max(dp[i−1][j],dp[i][j−1])dp[i][j] = \max(dp[i-1][j], dp[i][j-1])dp[i][j]=max(dp[i−1][j],dp[i][j−1])nums1的当前元素或nums2的当前元素,取较大值
-
初始化
-
dp[0][*] = 0 -
dp[*][0] = 0
答案
-
最终
dp[m][n](m 和 n 是两个数组的长度)即为最大不相交直线数。
class Solution:def maxUncrossedLines(self, nums1: List[int], nums2: List[int]) -> int:#如果两条线不相交,说明连接的数字在两个数组中 顺序一致。#这与 LCS 的定义完全一致(顺序相同,不要求连续)。m = len(nums1)n = len(nums2)dp = [[0]*(n+1) for _ in range(m+1)]for i in range(1, m+1):for j in range(1, n+1):if nums1[i-1] == nums2[j-1]:dp[i][j] = dp[i-1][j-1]+1else:dp[i][j] = max(dp[i][j-1], dp[i-1][j])return dp[-1][-1]3.最大子序和
53. 最大子数组和 - 力扣(LeetCode)
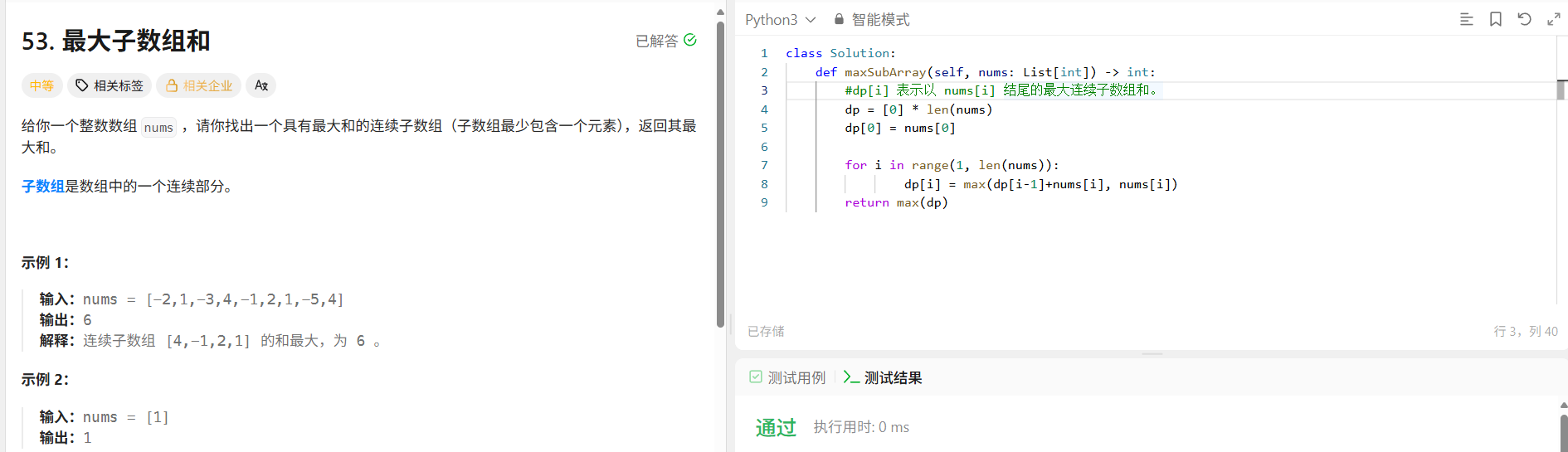
最大子数组和(Maximum Subarray)动态规划思路总结
1. 问题定义
给定整数数组 nums,找到一个连续子数组,使其元素和最大,返回该最大和。
2. 状态定义
-
dp[i]表示以nums[i]结尾 的连续子数组的最大和。
3. 状态转移方程
dp[i]=max(dp[i−1]+nums[i], nums[i])dp[i] = \max(dp[i-1] + nums[i],\ nums[i])dp[i]=max(dp[i−1]+nums[i], nums[i])
-
两种选择:
-
扩展之前的子数组(即加上当前元素)
-
从当前元素重新开始(放弃之前的和)
-
4. 初始化
dp[0]=nums[0]dp[0] = nums[0]dp[0]=nums[0]
5. 结果
-
最大子数组和为:
max0≤i<ndp[i]\max_{0 \leq i < n} dp[i]0≤i<nmaxdp[i]
6. 算法复杂度
-
时间复杂度:O(n)O(n)O(n) ,只需遍历一次数组。
-
空间复杂度:O(n)O(n)O(n),存储状态数组,可优化为 O(1)O(1)O(1) 使用滚动变量。
7. 贪心思想
-
在动态规划中体现为“如果之前的累计和是负数,则舍弃之前的和,从当前元素重新开始”,局部最优保证全局最优。
两种解法:
第一种动态规划:
class Solution:def maxSubArray(self, nums: List[int]) -> int:#dp[i] 表示以 nums[i] 结尾的最大连续子数组和。dp = [0] * len(nums)dp[0] = nums[0]for i in range(1, len(nums)):dp[i] = max(dp[i-1]+nums[i], nums[i])return max(dp)第二种贪心:
class Solution:def maxSubArray(self, nums: List[int]) -> int:#最大和的连续子数组#只要连续和不是负数,一直往后加Sum = 0result = float('-inf')for i in range(len(nums)):if Sum >= 0:Sum += nums[i]result = max(Sum, result)else:Sum = nums[i]return result4.判断子序列
392. 判断子序列 - 力扣(LeetCode)
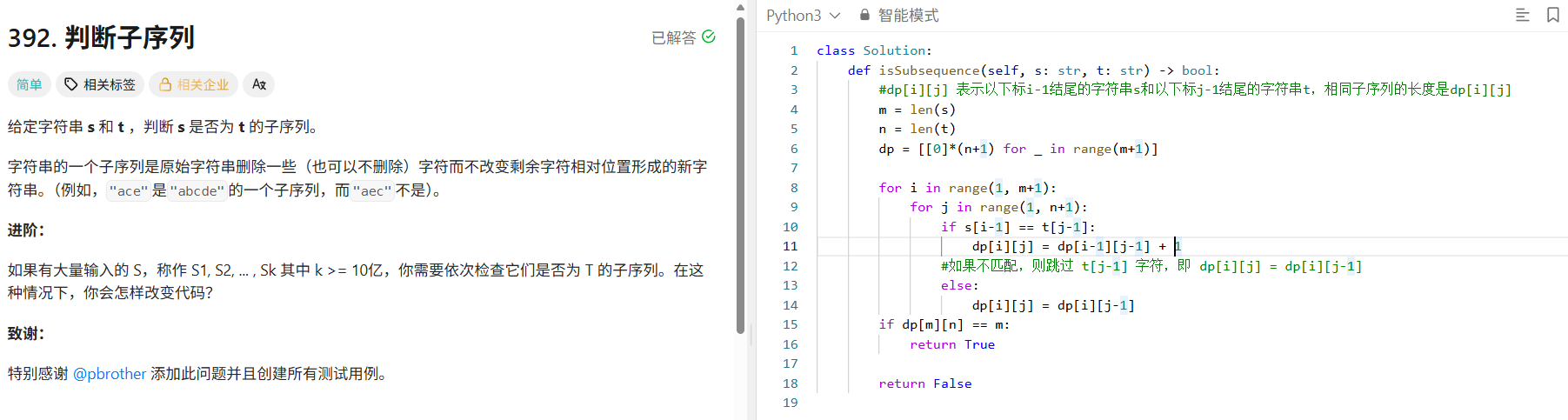
class Solution:def isSubsequence(self, s: str, t: str) -> bool:#dp[i][j] 表示以下标i-1结尾的字符串s和以下标j-1结尾的字符串t,相同子序列的长度是dp[i][j]m = len(s)n = len(t)dp = [[0]*(n+1) for _ in range(m+1)]for i in range(1, m+1):for j in range(1, n+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + 1#如果不匹配,则跳过 t[j-1] 字符,即 dp[i][j] = dp[i][j-1]else:dp[i][j] = dp[i][j-1]if dp[m][n] == m:return Truereturn False另一种双指针写法:
class Solution:def isSubsequence(self, s: str, t: str) -> bool:i, j = 0, 0while i < len(s) and j < len(t):if s[i] == t[j]:i += 1j += 1return i == len(s)
今天结束!
