回归分析预测原神深渊血量
想到一个乐子,随便试一下
能不能用回归分析,用原神以前的深渊总血量,来预测6.0版本的深渊血量?
6.0版本深渊总血量已知,正好可以看看预测结果对不对
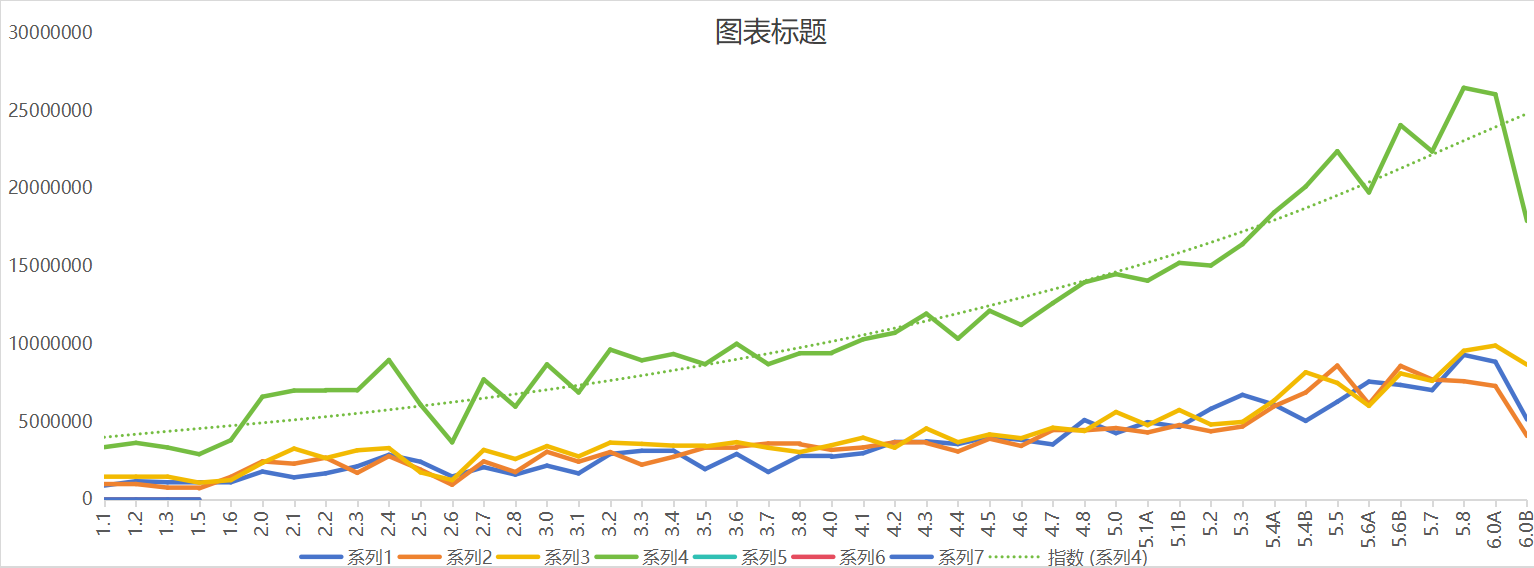
首先我们找到全部的数据并用excel绘制走势图
绿色的实线代表总血量走势,是下面三条线之和。绿色的虚线是excel给的指数拟合
当然这个图看起来不能确定用哪一种,还有多项式和线性看起来似乎也可以
于是我又试了一下线性回归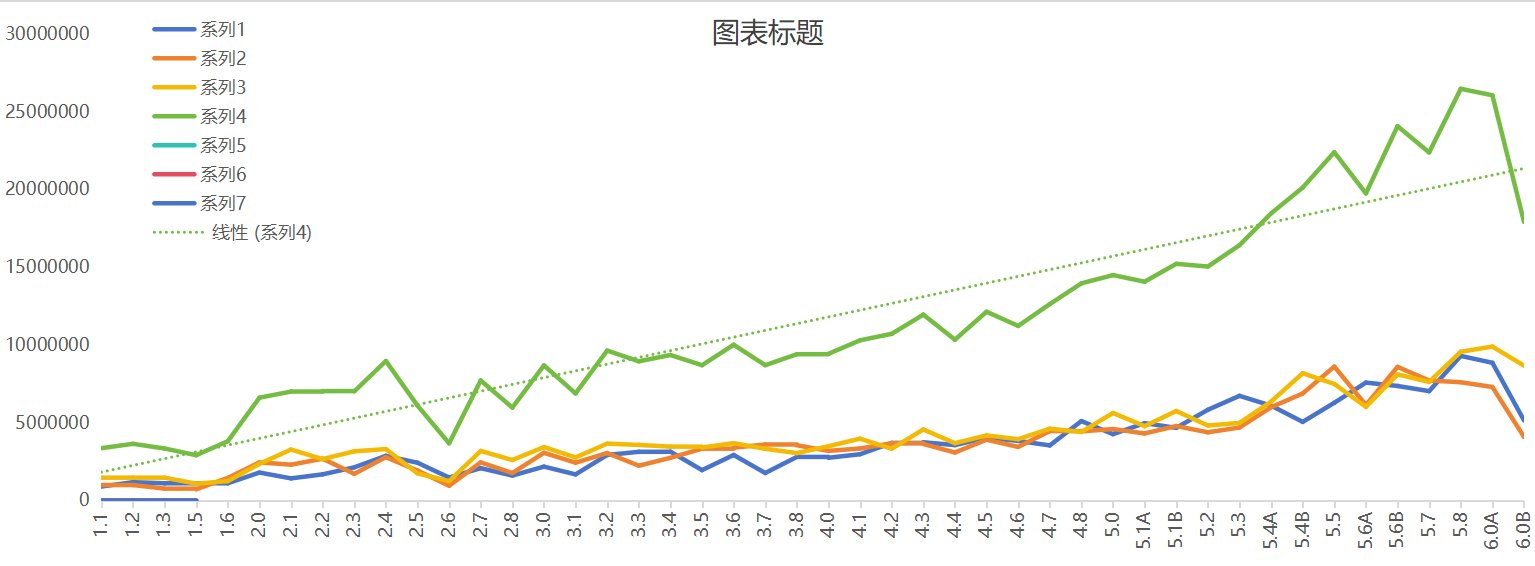
既然都有可能那就全试一下最后看R^2,谁最接近1说明谁拟合的越好
这里补充一下
R²,也称为决定系数或判定系数,是统计学中用于评估回归模型的一个重要指标。它用于衡量模型解释的因变量(Y)的变异占因变量总变异的比例。换句话说,R² 反映了自变量(X)对因变量(Y)的解释程度。
R² 的计算公式为:R² = 1 - (SSR/SST)
其中:
SSR(残差平方和) :模型预测值与实际值之间的差异平方和,反映了模型未能解释的变异。
SST(总平方和) :实际值与实际值的均值之间的差异平方和,反映了因变量的总变异。
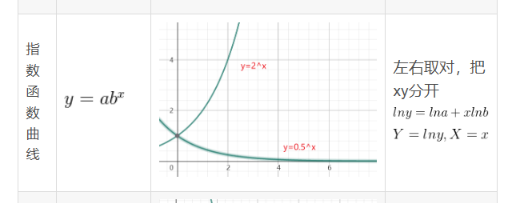
指数回归
我首先试了一下指数,因为图像看起来有点指数函数的感觉
%原神血量预测
x=[1:44];
y=[3368835
3646324
3347015
2914993
3816234
6612764
7008658
7038076
7018828
8973175
6103248
3680302
7722773
5978459
8690973
6888033
9643900
8952025
9358126
8702674
10018194
8703887
9408767
9437320
10304830
10720699
11955199
10344277
12142701
11229284
12631702
13969149
14496683
14073019
15220914
15047445
16420784
18464679
20127613
22399556
19750011
24075764
22385366
26477583
];
%指数回归类
Y=log(y);
X=[ones(44,1) x'];
alpha=0.05;
[b, bint, r, rint, stats] = regress(Y, X);z = exp(b(1) + b(2)*x);
plot(x, y,'k.',x,z,'r')最后

R^2达到了0.891,还不错,F=343.3034说明模型显著,p=0小于0.05说明模型可以接受
图像看起来还是很不错的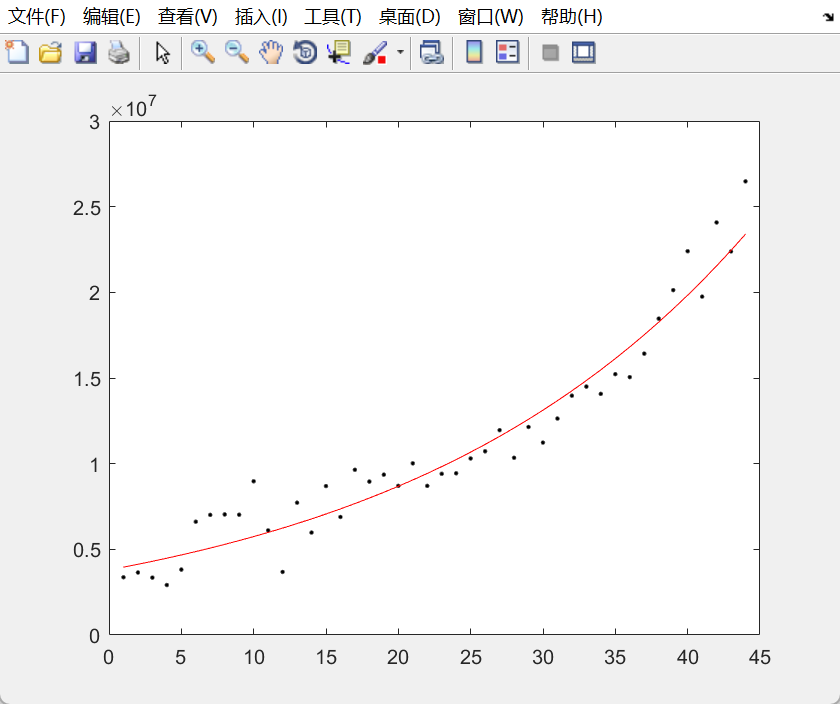
最后给出的公式是
也就是
6.0版本对应的x是45
带入得到y=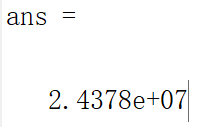 也就是24378000,实际上6.0A的血量是26059783
也就是24378000,实际上6.0A的血量是26059783
线性回归
然后试一下线性拟合
[b, bint, r, rint, stats] = regress(y, [ones(44,1) x'])
z = b(1) + b(2)*x;
plot(x, y,'k.',x,z,'r')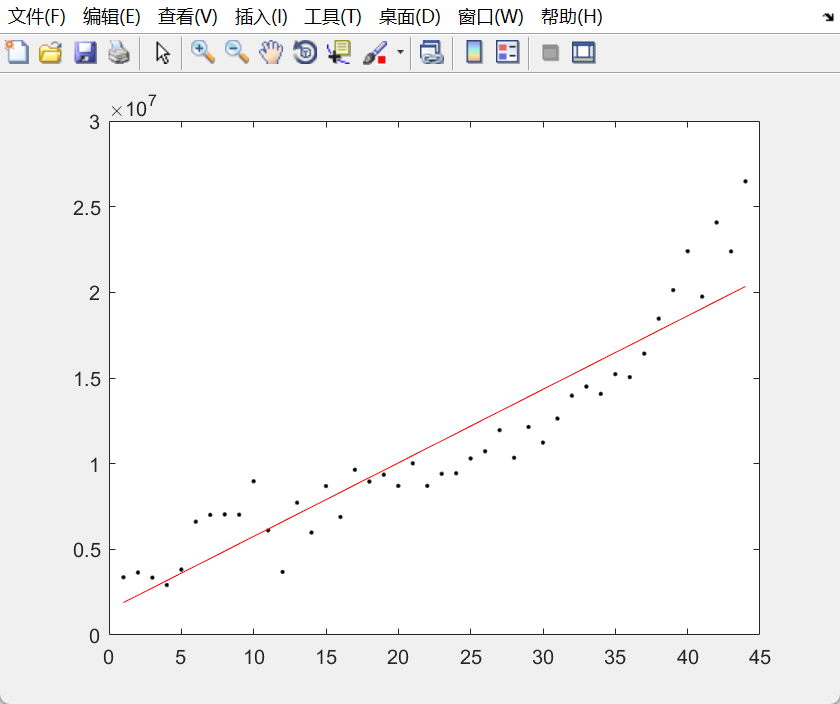

可以看得出来误差非常的大,说明这个模型不是很行,不过还是算一下结果
,带入45得到y=20777700
多项式回归
由于不确定x取到几次最好所以我们把1-10全试一下
% 创建图形窗口
figure;
%多项式回归
for n=1:10%假设多项式最多到10次方subplot(2, 5, n); % 参数:行数, 列数, 当前位置[p,S] = polyfit(x, y', n)Y=zeros(1,44);np=0;%用于计算Ffor i=1:n+1Y=Y+p(n+2-i)*(x.^(i-1));if p(n+2-i)~=0np=np+1;endend R2=1-S.normr^2/sum(y.^2);Avgy=sum(y)/44;SSR=sum((Y-Avgy).^2);F=(SSR/np)/(S.normr^2/(44-np-1));% 绘图plot(x, y,'k.',x,Y,'r')title(['Plot ', num2str(i)]);grid on;% 添加统一标签(可选)if i == 9 || i == 10 % 最后一行加x轴标签xlabel('X-axis');endif mod(i,2) == 1 % 第一列加y轴标签ylabel('Y-axis');end%计算预测值forcast=0;for i=1:n+1forcast=forcast+p(n+2-i)*(45^(i-1));end text(0.05, 0.95, ['R^2 = ' num2str(R2, '%.4f')], ...'Units', 'normalized', ... % 使用归一化坐标'BackgroundColor', [0.9 0.9 0.9], 'EdgeColor', 'k');text(0.05, 0.85, ['F = ' num2str(F, '%.4f')], ...'Units', 'normalized', ... % 使用归一化坐标'BackgroundColor', [0.9 0.9 0.9], 'EdgeColor', 'k');text(0.05, 0.75, ['预测值 = ' num2str(forcast, '%.4f')], ...'Units', 'normalized', ... % 使用归一化坐标'BackgroundColor', [0.9 0.9 0.9], 'EdgeColor', 'k');end

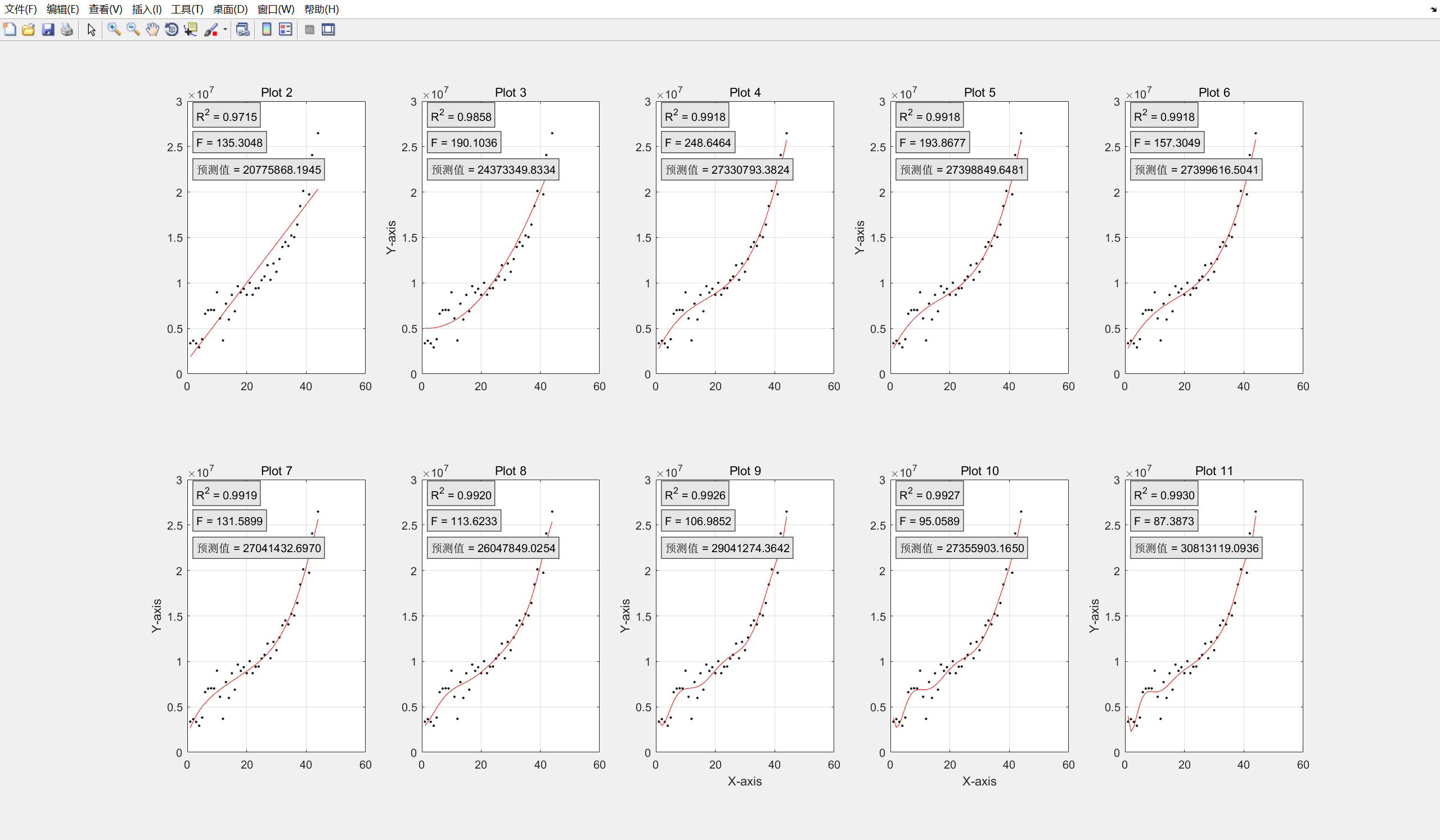
我们可以看到R^2和F不能同时达到最佳,所以理论上plot4最好(这个可以参考之前赋予权重来选择最优),计算结果是2733w,虽然和2605w有差距但是毕竟是预测值,真实情况还会存在其他影响。plot8最为准确,与实际结果仅仅相差1w
总结:
预测只能根据趋势预测个大概
实际多少血还得看ch心情,不过总体肯定还是有上升趋势的
灰色预测
等6.0出完还可以根据以前5个版本的平均值做灰色预测,也可以估算出6版本的平均水平
%灰色关联分析,原神
x=[1:5];
y=[3418680;6681809;8929619;11415017;19078284];
sumy=y;
for i=2:5sumy(i)=sumy(i)+sumy(i-1);
end
% plot(x,sumy,'k.');
%判断是否通过级比检验
test=1;
exp(2/(size(x,2)+1))
for i=2:5lambda=sumy(i-1)/sumy(i);if lambda>exp(2/(size(x,2)+1))||lambda<exp(-2/(size(x,1)+1))test=0;end
end
if test==1disp('pass');
elsedisp('can not use');
end但是这个连级比检验都没过,只能平移比如基数加一点之类的再算
实际上这种数据完全可以用上面的几种预测
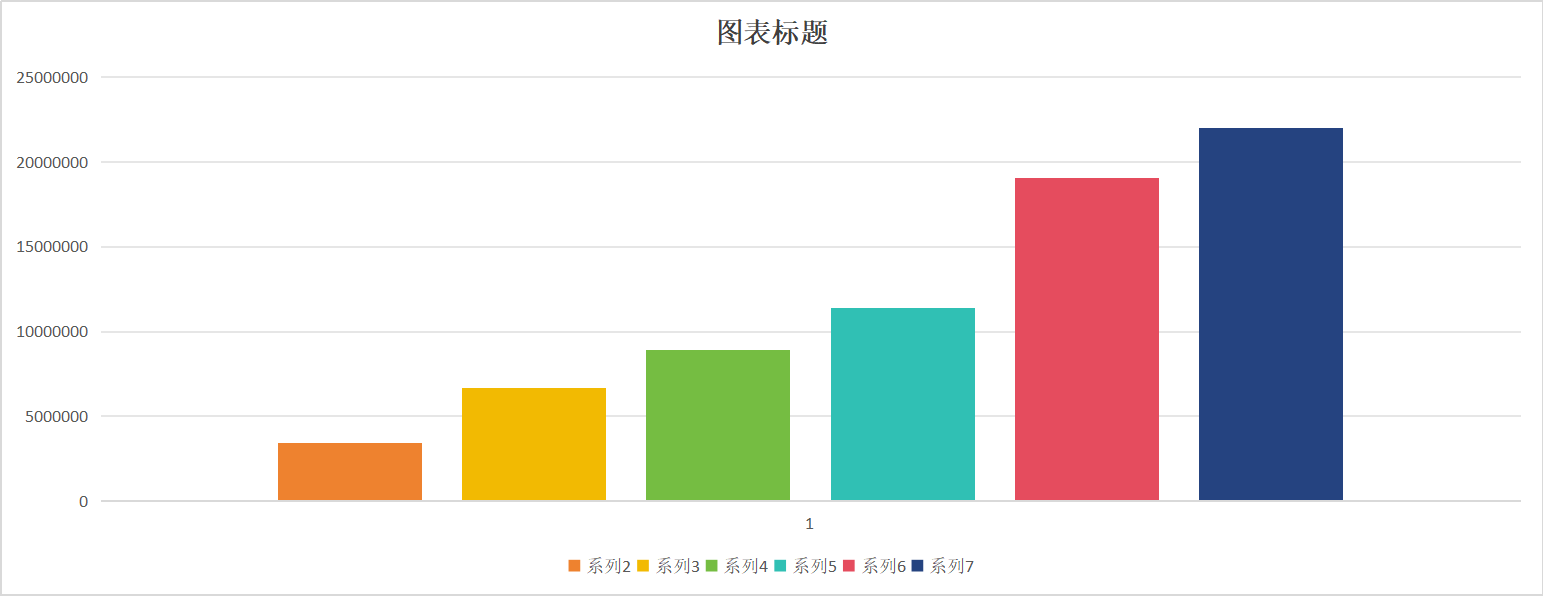
有明显规律,其实都不太需要灰色预测,灰色预测一般是有的点数值很奇怪,或者变化无规律才会使用
所以就不往下深究了,这里只需要改一下y值套用一下上面的代码就可以计算
补充:(deepseek)




