力扣hot100 | 双指针 | 283. 移动零、11. 盛最多水的容器、42. 接雨水

283. 移动零

力扣题目链接
给定一个数组nums，编写一个函数将所有0移动到数组的末尾，同时保持非零元素的相对顺序。
请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例：
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]

一、快慢指针法（交换式）

市面上的标准解法。

1. fast遍历整个数组，slow指向下一个非零元素应该放置的位置；
2. 当fast指向非零元素时，将其与slow位置的元素交换，并且slow前进1，（fast也前进1）；
3. （fast指向0时，slow停滞而且不交换，只有fast还往前走）；
4. （下一轮若fast指向非零，则slow位置的0会被交换到后面，所以不用最后还填充0）。

class Solution:def moveZeroes(self, nums: List[int]) -> None:"""Do not return anything, modify nums in-place instead."""slow = 0  # 定义慢指针for fast in range(len(nums)):  # 定义快指针if nums[fast] != 0:nums[slow], nums[fast] = nums[fast], nums[slow]slow += 1 return nums

• 时间复杂度 O(n)
• 空间复杂度 O(1)

二、快慢指针（覆盖式）

自己想的所以比较丑陋，但复杂度其实不变。

• 【区别】法一通过nums[fast]判断慢指针是否前进, 法二却根据nums[slow]判断。
• 【思路】先用快指针的元素覆盖慢指针的位置（“只完成交换操作的一半”），再填充最后的0。

class Solution:def moveZeroes(self, nums: List[int]) -> None:"""Do not return anything, modify nums in-place instead."""fast, slow = 0, 0 # 定义快慢指针for _ in range(len(nums) - 1):  # 注意边界！fast += 1if nums[slow] != 0:slow += 1nums[slow] = nums[fast]for i in range(slow+1, len(nums)):  # 只把剩下的遍历了，没有从头再来哦nums[i] = 0return nums

• 时间复杂度 O(n)
• 空间复杂度 O(1)

11. 盛最多水的容器

力扣题目链接
给定一个长度为n的整数数组height。有n条垂线，第i条线的两个端点是(i, 0)和(i, height[i])。

找出其中的两条线，使得它们与x轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例：
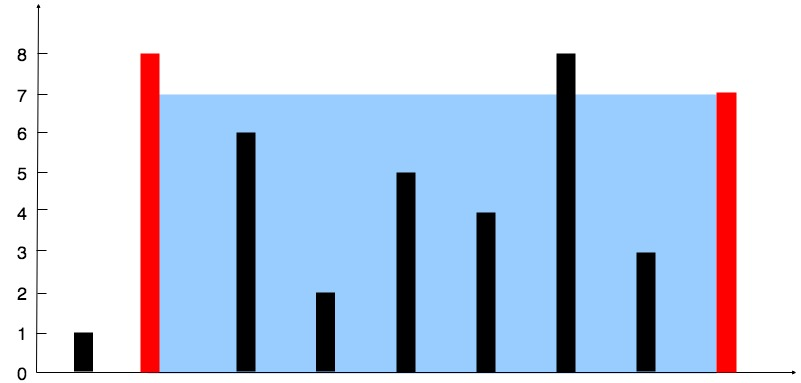
输入：[1,8,6,2,5,4,8,3,7]
输出：49
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

一、暴力法（仅用于理解题意）

直接两层嵌套枚举

    def maxArea_brute_force(self, height):max_water = 0n = len(height)for i in range(n):for j in range(i + 1, n):width = j - icurrent_height = min(height[i], height[j])current_area = width * current_heightmax_water = max(max_water, current_area)return max_water

• 时间复杂度 O(n²)
• 空间复杂度 O(1)

二、双指针

【思路】：

1. 左右两指针分别指向数组的开始和结束，在while left < right中一直向内收缩即可（不回头）！
2. 计算当前容器的面积
3. 移动高度较小的那个指针（因为移动高度大的指针不可能得到更大面积）—— “容量取决于短板”
4. 持续更新最大面积

class Solution:def maxArea(self, height: List[int]) -> int:left, right = 0, len(height) - 1max_water = 0while left < right:# 计算当前容器面积width = right - leftcurr_height = min(height[left], height[right])curr_area = width * curr_height# 更新最大面积max_water = max(max_water, curr_area)# 移动高度较小的指针if height[left] < height[right]:left += 1else:right -= 1return max_water

• 时间复杂度 O(n)
• 空间复杂度 O(1)

为什么双指针不用“回头”？

Q：为什么我们可以确信双指针从两端向内收缩就能找到最优解，而不需要考虑指针"回头"（左指针向左移动，右指针向右移动）的情况？
A：每次移动都会永久排除一批不可能的解。下面证明为什么被排除的组合永远不是最优解：

假设当前状态是 (left, right)，且 height[left] < height[right]。
根据算法，我们会执行 left++，即从 (left, right) 移动到 (left+1, right).

• 关键问题： 我们是否会错过以 left 为左边界的其他组合？
  被跳过的组合有：(left, right-1), (left, right-2), …, (left, left+1)
• 证明这些组合都不会是最优解： 对于任意被跳过的组合 (left, k) 其中 left < k < right：

1. 宽度比较：k - left < right - left（宽度更小）
2. 高度比较：min(height[left], height[k]) ≤ height[left]（高度不会更大）
3. 面积比较：
   Area(left, k) = min(height[left], height[k]) × (k - left)
   ≤ height[left] × (k - left)
   < height[left] × (right - left)
   = min(height[left], height[right]) × (right - left)
   = Area(left, right)
   因此，Area(left, k) < Area(left, right)，所以这些被跳过的组合不可能比当前组合更优。

42. 接雨水

力扣题目链接
给定n个非负整数表示每个宽度为1的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

参考解析视频

【核心思路】对于位置 i，能接的雨水量 = min(左侧最高柱子, 右侧最高柱子) - height[i]

一、前后缀分解（预处理max前后缀 + 从头遍历）

【算法步骤】（其实也是双指针，只不过是在预处理阶段分开遍历了）
1. 预处理：计算每个位置i左侧的最大高度（前缀最大值）
2. 预处理：计算每个位置i右侧的最大高度（后缀最大值）
3. 遍历每个位置，计算该位置能接的雨水量

class Solution:def trap(self, height: List[int]) -> int:n = len(height)# 1. 建立最大前缀数组pre_max = [0] * npre_max[0] = height[0] # 一定要现有一个初始值！！才能开始累积比较！！for i in range(1, n):pre_max[i] = max(pre_max[i - 1], height[i]) # 当前高度h[i]与前一个max值比！# 2. 建立最大后缀数组suf_max = [0] * nsuf_max[-1] = height[-1]  # 别忘了这里是从后往前！！从最后一个开始设初始值！！for i in range(n-2, -1, -1):  # 从倒数第二个倒着开始！suf_max[i] = max(suf_max[i + 1], height[i])# 3. 遍历所有位置的雨水量total = 0for h, pre, suf in zip(height, pre_max, suf_max):total += min(pre, suf) - hreturn total

• 时间复杂度 O(n)
• 空间复杂度 O(n)

二、相向双指针（边收缩边计算，哪边矮就先 移动/计算 哪边）

【思路】不用预处理max前后缀，在while left < right中不断向内收缩，边遍历边计算当前左右指针（其中之一）处的雨水量即可。

• 法一的计算顺序是从左往右；法二则是从外向内、左右摇摆的。
• 法一相当于双指针都遍历了全程（后面有交叉）；法二则相当于省去了交叉后的部分，仅遍历到相遇为止。

【算法步骤】
1. 设左右两个指针从两端向中间移动，while left < right；
2. 更新左右两侧的最大高度；
3. 根据判断，更新计算与移动：
① 左侧较矮算左边，左指针位置的水位由 max_left 决定（max_l - height[left]）、移动left；
② 右侧较矮算右边，右指针位置的水位由 max_right 决定（max_r - height[right]）、移动right。

class Solution:def trap(self, height: List[int]) -> int:left, right = 0, len(height) - 1max_l = max_r = 0total = 0while left < right:max_l = max(max_l, height[left])max_r = max(max_r, height[right])if max_l <= max_r:total += max_l - height[left]left += 1else:total += max_r - height[right]right -= 1return total

• 时间复杂度 O(n)
• 空间复杂度 O(1)：不用提前建立两个max前后缀数组。