2025年中科院2区红杉优化算法Sequoia Optimization Algorithm-附Matlab免费代码

1. 简介

提出了红杉优化算法（SequoiaOA），这是一种受红杉森林生态系统自我调节动力学和弹性启发的新型元启发式方法，不同于传统的奇异生物学或现象学灵感。开发一个全面的生态系统驱动框架，包括数学建模、系统分析和通过CEC基准测试和多约束工程问题进行验证。当前的元启发式算法通常局限于来自单一视角、孤立的生物行为或个体现象的灵感，导致了推动本研究的内在局限性。与传统方法不同，本文从生态系统的角度探索复杂的生物系统，并进行全面的系统建模、分析和算法创新。具体而言，提出了一种受红杉森林生态系统中观察到的自我调节和恢复现象启发的新型元启发式优化算法，称为红杉优化算法（SequoiaOA）。红杉生态系统表现出包括集体生长、资源共享和网络、适应性和弹性、繁殖和多样性以及精英保留在内的鲜明特征。基于这些现象，这项工作提出了SequoiaOA的第一个公式，从生态系统复杂性、自我调节和宏观系统弹性的角度，通过算法建模和验证来开发其数学模型和工程应用。

2.红杉优化算法

红杉的生态环境主要由这些非凡的巨人组成，也被称为海岸红杉，它们属于柏树科的红杉属。成熟的红杉在温暖、潮湿和阳光充足的环境中茁壮成长，可以达到70-120m的高度，寿命从800年到3000年不等，使它们成为世界上最非凡的自然奇观之一。在这种生态环境中，红杉表现出显著的适应性和复原力。这一点可以从它们厚厚的树皮和低树脂含量以及海绵状的吸水能力中得到证明，这赋予了它们对疾病和火灾的高抵抗力。此外，红杉表现出强大的生命力，其特点是快速生长和高成活率。即使被砍伐或损坏，红杉也可以通过从毛刺中长出新树来再生。红杉树的图像可以从参考文献[105]中获得。
在红杉的生态环境中，集体生长、资源共享和网络的强烈存在。这一点的例证是这些树木经常生长的密集集群，在保持土壤水分的同时提供相互保护以抵御强风和侵蚀。如果红杉倒下或死亡，邻近的树木可以通过相互连接的根网络支持新树苗的生长，从倒下的“母亲”树的根部汲取水和养分。这种互利关系促进了个体的生存和群体的复原力[106]。红杉的浅而广泛的根系与周围的植物和真菌形成共生网络，促进了水和养分的共享交换。
在红杉生态环境中，也非常强调繁殖和多样性，以及精英保留。红杉厚厚的树皮和蓄水能力使它们能够忍受火灾，并通过再生迅速恢复。繁殖是通过种子传播实现的，保持遗传多样性，并能够适应不断变化的环境条件。虽然火灾可能会破坏一些植被，但它们也会促进种子萌发，维持红杉生态系统的持续发展。红杉优化算法的灵感来自红杉树的这些生长行为和弹性特征，其数学模型概述于以下部分。

2.1 初始化

与其他群体智能（SI）算法类似，红杉优化算法（Sequoia OA）首先在解空间中初始化一组候选解。每个候选解代表一棵红杉树，如公式（1）所示：

$$X=[x_1,x_2,\dots ,x_D]\text{\hspace{1em}(1)}$$

其中$D$表示问题的维度。对于最小化问题，所有解如公式（2）所示，其中适应度值最小的红杉树解被视为当前迭代的最优解。若当前最优解的适应度值更小，则用其替换历史最优解。

$$X_{pop}=\left[\begin{array}{ccccc}{x}_{1,1}& x_{1,2}& \dots & x_{1,D-1}& x_{1,D}\\ x_{2,1}& x_{2,2}& \dots & x_{2,D-1}& x_{2,D}\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ x_{N-1,1}& x_{N-1,2}& \dots & x_{N-1,D-1}& x_{N-1,D}\\ x_{N,1}& x_{N,2}& \dots & x_{N,D-1}& x_{N,D}\end{array}\right]\text{\hspace{1em}(2)}$$

其中$X_{pop}$表示由红杉树群体组成的解，通过公式（3）初始化，而$1D$红杉树种群的完整位置，$N$表示红杉树种群的数目。

$$x_i=B+\text{rand}(B,1)\times (a-b)\text{\hspace{1em}(3)}$$

其中$x_i$表示个体$i$的位置或解向量，$a$和$b$表示优化问题的上下界，$\text{rand}(B,1)$生成一个0到1之间的随机数，表示个体在上下界之间的随机分布。

2.2 数学模型

2.2.1 集体生长资源共享与网络

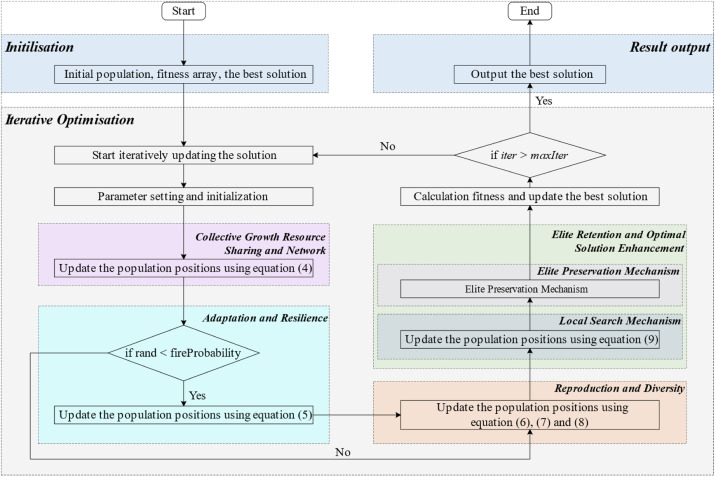
红杉树以集群方式生长，形成茂密的森林。其根系既浅又广，与周围的植物和真菌建立共生网络，共享水分和养分。这种集体行为提供了抵御环境压力的保护，根系网络的资源共享使得群体内能够合作与互助。受此群体行为启发，算法设计可以增强地下资源共享机制作为一种协作调整策略。该策略通过群体中的个体向最优解靠拢，促进信息进一步共享，如公式（4）所示。通过计算群体中表现最优的一半个体的均值，引导整个群体向更优解靠近，模拟红杉树的资源共享机制。这种方式利用优秀个体的均值调整所有个体的解，通过促进整体优化过程实现有效的信息共享与合作。

$$x_i=n_i+\text{random}(0,1)\times ({\Sigma }_{top}-x_i)\text{\hspace{1em}(4)}$$

其中$n_i$表示个体$i$的位置或解向量，$\text{random}(0,1)$表示从正态分布生成一个随机数，用于估计扰动${\Sigma }_{top}$表示群体中表现最优的一半个体的平均位置，总结了群体的集体知识。

2.2.2 适应性与韧性

红杉树以其卓越的适应性闻名。在干旱和火灾等极端环境中，其厚实的树皮和出色的储水能力使其能够抵御火灾并迅速恢复。红杉生长的生态系统常受火灾事件影响。尽管火灾可能对某些植被具有破坏性，但其清除了较弱的竞争者，将养分释放到土壤中，并刺激红杉种子的萌发。这一生长过程增强了森林的生物多样性和韧性。受此自然过程启发，如公式（5）所示，算法设计引入了随机分布机制以模拟此类环境扰动。通过引入随机扰动，算法能够逃离局部最优并探索更广阔的解空间，避免群体过早收敛。火灾扰动机制是算法设计中的关键策略，增强了全局搜索能力和鲁棒性。通过精确控制扰动概率，该方法确保扰动频率既不会过高而影响收敛速度，也不会过低而陷入局部最优。

$$x_i=x_i+\text{random}(0,1)\times 0.5\text{if }(\text{rand}<\text{fireProbability})\text{\hspace{1em}(5)}$$

其中$\text{fireProbability}(Fy)$表示火灾扰动的概率，定义为$Fy=\max (0.5-0.5\times \frac{\text{iter}}{\text{maxIter}})$。概率随迭代次数调整，并为群体中的每个个体分配随机分布。$\text{random}(0,1)$用于从正态分布引入随机扰动，模拟火灾后的环境变化。$x_i$表示个体$i$的位置或解向量。$0.5$表示扰动幅度系数，控制扰动的强度。$\text{iter}$为当前迭代次数，$\text{maxIter}$为最大迭代次数，$\max (0,b)$表示取$a$和$b$的最大值，确保参数不低于特定阈值。

2.2.3 繁殖与多样性

受红杉树通过种子传播繁殖并维持遗传多样性以适应环境变化的启发，算法采用交叉和变异机制。通过模拟生物繁殖中的基因重组和突变，这些机制引入多样性并增强适应性，从而提高解的全面性。交叉使得有利特征得以传递和组合，而变异提供了新的探索方向，避免过早收敛。这种繁殖机制通过交替进行交叉和变异，使算法能够以更多样化的方式探索搜索空间，增加找到全局最优解的可能性。

(1) 交叉

交叉是指从两个父代个体生成一个或多个后代的过程。交叉操作使得父代个体的特征得以重组和传递，使下一代能够继承父代的有利特征。交叉操作的过程增加了群体的多样性，并有助于逃离局部最优。在算法设计中，如公式（6）和（7）所示，交叉操作通过两个父代个体的线性组合实现：

$${\text{offspring}}_1=a\times x_i+(1-a)\times x_j\text{\hspace{1em}(6)}$$

$${\text{offspring}}_2=a\times x_{i+1}+(1-a)\times x_j\text{\hspace{1em}(7)}$$

其中$x_i$表示个体$i$的基因。${\text{offspring}}_1$和${\text{offspring}}_2$表示交叉后生成的两个后代，$a$表示一个0到1之间随机生成的权重系数，用于两个个体基因的线性组合。通过随机系数$a$实现交叉，并通过添加随机扰动引入变异以增加解的多样性。

(2) 变异

变异通过对个体进行随机调整以引入新的遗传特征。该操作增强了解的多样性，防止群体收敛至局部最优。通过施加随机扰动，算法能够探索解空间的新区域，帮助逃离局部最优陷阱。变异操作如公式（8）所示：

$$\text{offspring}=\text{offspring}+\text{randn}(1,\text{dim})\times 0.3\text{if }(\text{rand}<\text{mutationRate})\text{\hspace{1em}(8)}$$

其中$\text{mutationRate}(m_r)$表示变异发生的概率，定义为$m_r=\max (0.2-0.1\times \frac{\text{iter}}{\text{maxIter}},0.02)$。变异率决定每个后代是否进行变异。$\text{randn}(1,\text{dim})$表示生成一个与个体维度相同的向量，其每个元素为标准正态分布的随机数。$\text{iter}$为当前迭代次数，$\text{maxIter}$为最大迭代次数。函数$\max (a,b)$返回$a$和$b$中的较大值，确保参数不低于特定阈值。

2.2.4 精英保留与最优解增强

受红杉树高大 stature 和长寿特性的启发（使得最强个体能够长期存活并繁殖），算法采用精英保留策略以保留最优解，确保最佳解在迭代过程中不被丢弃。同时，局部搜索机制模拟红杉对微环境的精细适应，帮助发现更优解。局部搜索与精英保留机制共同模拟了自然选择原则：局部搜索反映生物对微环境的适应，精英保留确保优良特征的传递。通过在每代中微调并保留最优解，这些机制提升了搜索过程的精度和稳定性。二者的结合实现了精细的局部探索与全局搜索的平衡，确保高质量解不被丢弃，从而提高算法的整体效率和鲁棒性。

(1) 局部搜索机制

局部搜索机制通过对当前最优解施加微小扰动，模拟红杉对局部环境的精细适应以发现更优解。具体数学表达式如公式（9）所示，其中对当前最优解施加小扰动生成新局部解，促进其邻域内的局部搜索。

$$x_{\text{local}}=x_{\text{best}}+0.1\times \text{randn}(0,1)\text{\hspace{1em}(9)}$$

其中$x_{\text{local}}$表示局部搜索后的解，$x_{\text{best}}$表示当前最优解的位置，$\text{randn}(1,\text{dim})$表示生成维度为$\text{dim}$的随机向量，其每个元素取自标准正态分布。

(2) 精英保留机制

精英保留机制通过保留精英个体至下一代，确保优良特征的继承。具体操作如下：首先根据适应度值对所有个体排序，然后从排序后的群体中选择前$\text{eliteSize}$个适应度值最高（最小化问题中为最低）的个体作为精英个体，最后用这些精英个体替换排序后前$\text{eliteSize}$个个体，使其进入下一代。此处$\text{eliteSize}$表示保留的精英个体数量。

2.2.5 SequoiaOA的流程图与伪代码

为清晰展示SequoiaOA的流程，图1提供了算法流程图，伪代码如算法1所示。

% Sequoia Optimisation Algorithm(SequoiaOA)
% Developed in MATLAB R2022b
function [bestFitness, bestSolution, convergenceCurve] = SequoiaOA(popSize, maxIter, lb, ub, dim, fobj)% Initial populationpopulation = repmat(lb, popSize, 1) + rand(popSize, dim) .* (repmat(ub - lb, popSize, 1));% initializes the fitness arrayfitness = zeros(popSize, 1);for i = 1:popSizefitness(i) = fobj(population(i, :));end% initializes the best solution[bestFitness, bestIndex] = min(fitness);bestSolution = population(bestIndex, :);% convergence curveconvergenceCurve = zeros(1, maxIter);% Start iteratively updating the solutionfor iter = 1:maxIter% Dynamically adjust parametersfireProbability = max(0.3 - 0.15 * (iter / maxIter), 0.1);mutationRate = max(0.2 - 0.1 * (iter / maxIter), 0.02);% Sorted by fitness[sortedFitness, sortedIndices] = sort(fitness);sortedPopulation = population(sortedIndices, :);population = sortedPopulation;eliteSize = 2;eliteSolutions = population(sortedIndices(1:eliteSize), :);% Collective Growth Resource Sharing and NetworkhalfPopSize = round(popSize/2);topIndividuals = population(1:halfPopSize, :);meanTop = mean(topIndividuals, 1);population = population + randn(popSize, dim) .* (repmat(meanTop, popSize, 1) - population);% Adaptation and Resilienceif rand < fireProbabilitypopulation = population + randn(popSize, dim) * 0.5;end% Reproduction and Diversityfor i = 1:2:popSizeif i + 1 ≤ popSize% Crossoveralpha = rand;offspring1 = alpha * population(i, :) + (1 - alpha) * population(i + 1, :);offspring2 = alpha * population(i + 1, :) + (1 - alpha) * population(i, :);% Mutationif rand < mutationRateoffspring1 = offspring1 + randn(1, dim) * 0.3;offspring2 = offspring2 + randn(1, dim) * 0.3;end% Boundary Treatmentoffspring1 = max(min(offspring1, ub), lb);offspring2 = max(min(offspring2, ub), lb);% Regeneration Populationpopulation(i, :) = offspring1;population(i + 1, :) = offspring2;endend% Local Search MechanismlocalBest = bestSolution + 0.1 * randn(1, dim);localBest = max(min(localBest, ub), lb);localFitness = fobj(localBest);if localFitness < bestFitnessbestFitness = localFitness;bestSolution = localBest;end% Elite Preservation Mechanismpopulation(sortedIndices(end-eliteSize+1:end), :) = eliteSolutions;% Calculation fitnessfor i = 1:popSizefitness(i) = fobj(population(i, :));end% update the best solution[currentBestFitness, currentBestIndex] = min(fitness);if currentBestFitness < bestFitnessbestFitness = currentBestFitness;bestSolution = population(currentBestIndex, :);end% Records the convergence curveconvergenceCurve(iter) = bestFitness;disp(['Iteration=' num2str(iter) ', Best Fitness=' num2str(bestFitness)]);end
end

Shijie Fan, Ruichen Wang, Kang Su, Yang Song, Rui Wang, A sequoia-ecology-based metaheuristic optimisation algorithm for multi-constraint engineering design and UAV path planning,Results in Engineering,Volume 26,2025,105130, https://doi.org/10.1016/j.rineng.2025.105130.