【12-激活函数】

激活函数的重要性

如果你在神经网络中的所有神经元都使用线性激活函数，事实证明，这个神经网络模型将和线性回归没有任何区别；

这样不如直接使用线性回归模型，没必要使用神经网络，线性函数的线性函数还是线性函数；

一个常见的经验法则：不要在神经网络的隐藏层中使用线性激活函数；

因为这样会导致这个神经网络能做什么完全取决于最后一个输出神经元，如果是线性函数，那就是线性回归模型，如果是sigmoid函数那就是逻辑回归模型；

其他激活函数

选择不同的激活函数，可以使得神经网络模型的功能更强大；

以T-shit销售为例，输入特征有四个，价格，运费，营销费，材料；第一层的神经元有三个，affordability, awareness, preceived quality;

而人们对某产品的知晓程度并不是二元的，而可以是任何非负数来表示；

ReLU激活函数

除了sigmoid的另一个常用激活函数是 g(z) = max(0, z); 它名字叫ReLU，代表校正线性单元；

如果使用的是线性激活函数比如g(z) = z; 一般认为没有使用任何激活函数，因为对于将z = wx +b 带入g(z) ，若g(z)为线性，则会发现其结果依然是wx + b 的形式；

选择激活函数

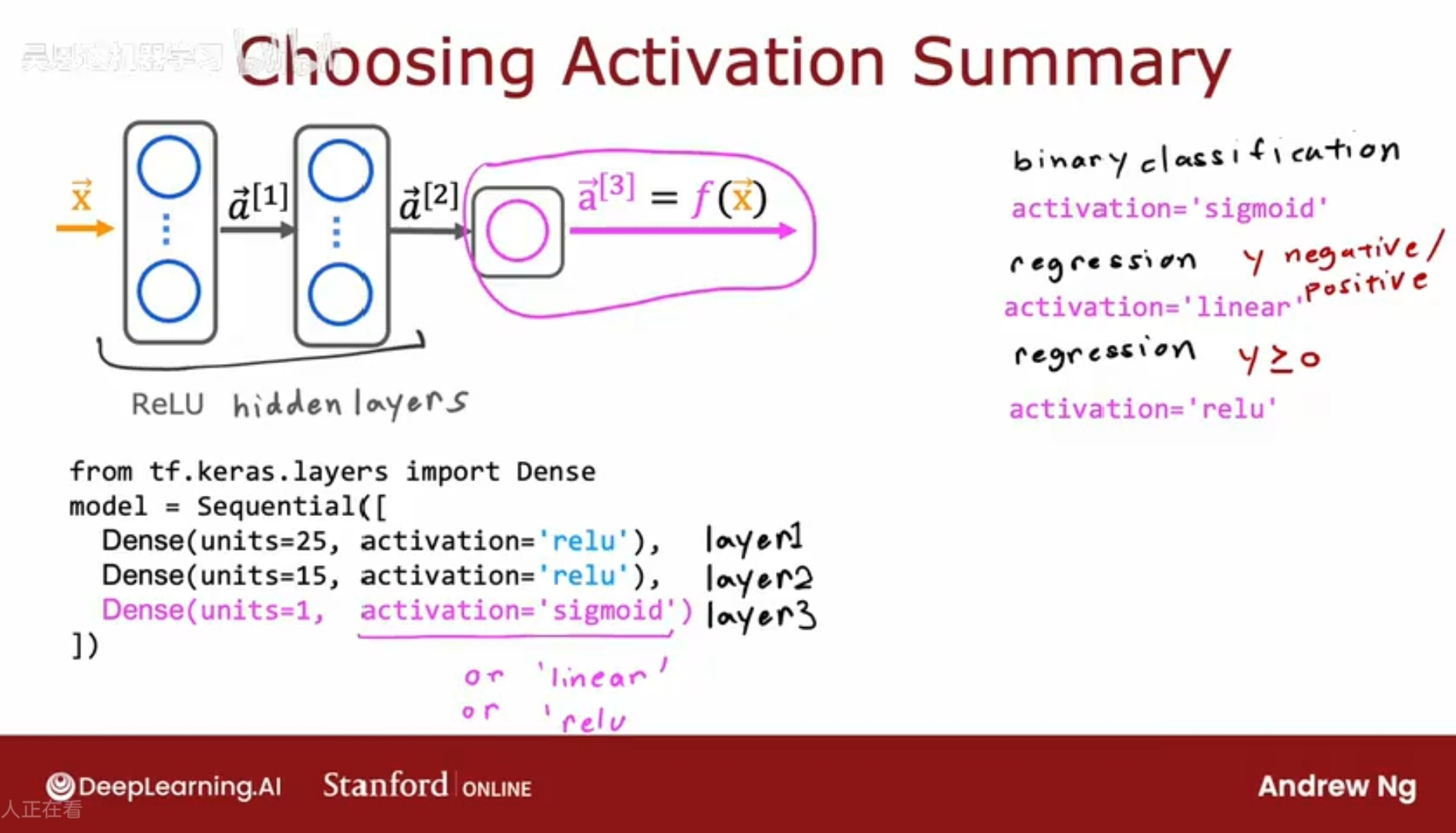
为输出层选择激活函数
考虑目标和真实标签Y，二元分类问题，就选择sigmoid函数；

解决回归问题，预测某个值；

Y是一个可正可负的数字，建议使用线性激活函数。

Y是一个正数，可选择ReLU函数。

为隐藏层选择激活函数

事实证明，ReLU激活函数是训练神经网络时最常见的选择；目前几乎都采用ReLU，只有在输出层是二进制时才使用sigmoid函数；

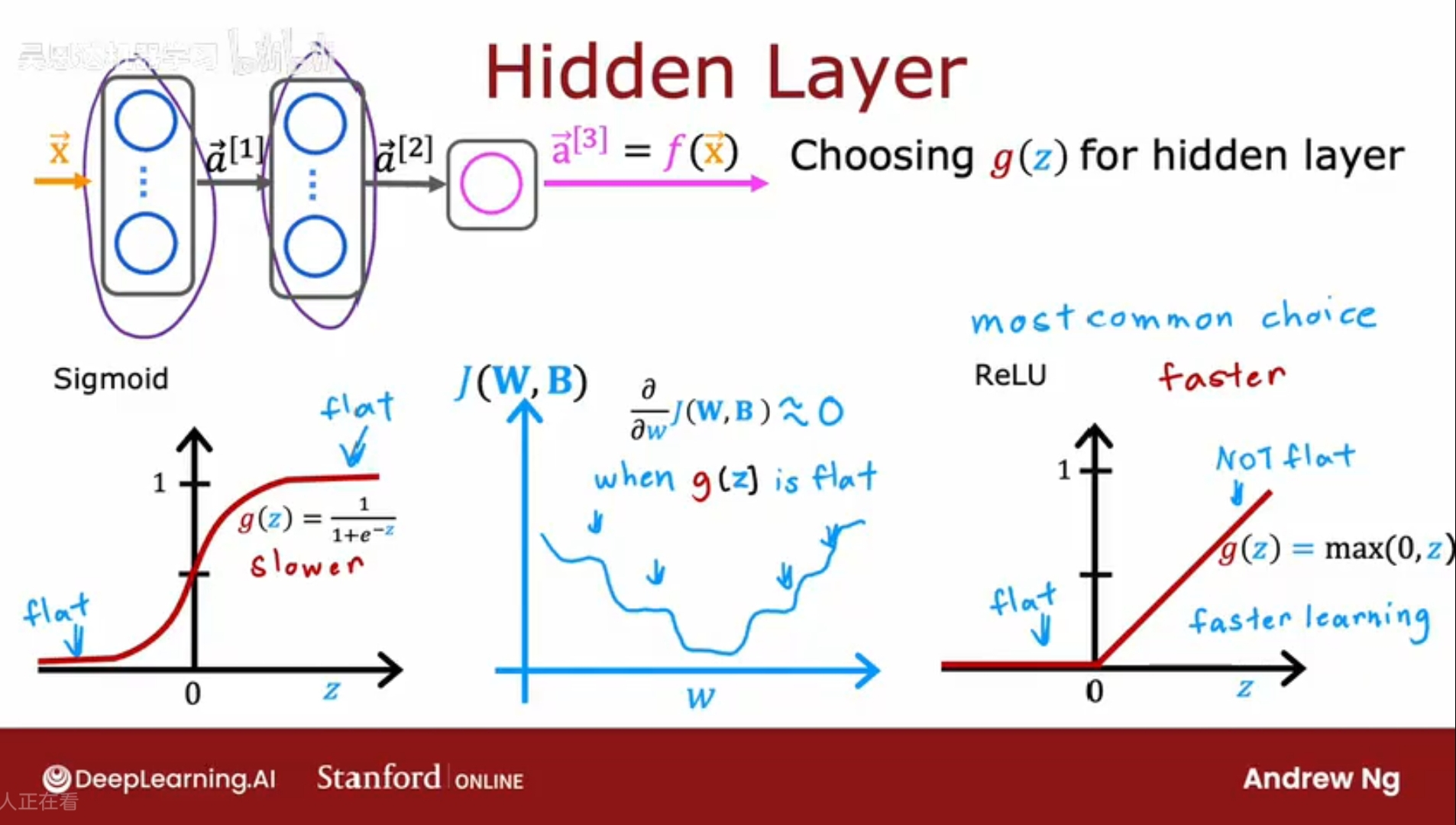
ReLU和Sigmoid的对比：

1、ReLU函数计算更快，比较运算明显快于指数运算；

2、ReLU函数是在<0是变平，而Sigmoid在两个地方变平，当使用梯度下降算法训练神经网络时，在变平的地方，梯度下降会非常慢；解释：g(z)是J的一部分，当g(z)变平时，J对w的偏导即变化率也变得很小，会减慢学习速度；

对于隐藏层，建议使用ReLU函数；