当前位置：首页 > news >正文

算法训练营day45 动态规划⑫ 115.不同的子序列、583. 两个字符串的删除操作、72. 编辑距离、编辑距离总结篇

news 2025/8/12 7:22:11

动态规划的十二篇博客，这篇博客来一点点引入“编辑距离”的问题

115.不同的子序列

感觉这道题看起来是很难的，因为感觉有很多重复的区域判定（我才发现，这道题目给出了待查找字符串t，我还以为要自己找t，我的天，认真读题），by the way,顺便复习了一下KMP算法，这个算法的主要目的是高效的字符串匹配，回到正题，我们来使用动态规划

帮你把KMP算法学个通透！（理论篇）_哔哩哔哩_bilibili

同时补充一下，这个题目和我们上一篇博客的最后一题是相似的，因为都只涉及减去元素的操作

算法训练营day44 动态规划⑪ 1143.最长公共子序列、1035.不相交的线、53. 最大子序和、392.判断子序列-CSDN博客

确定dp数组（dp table）以及下标的含义

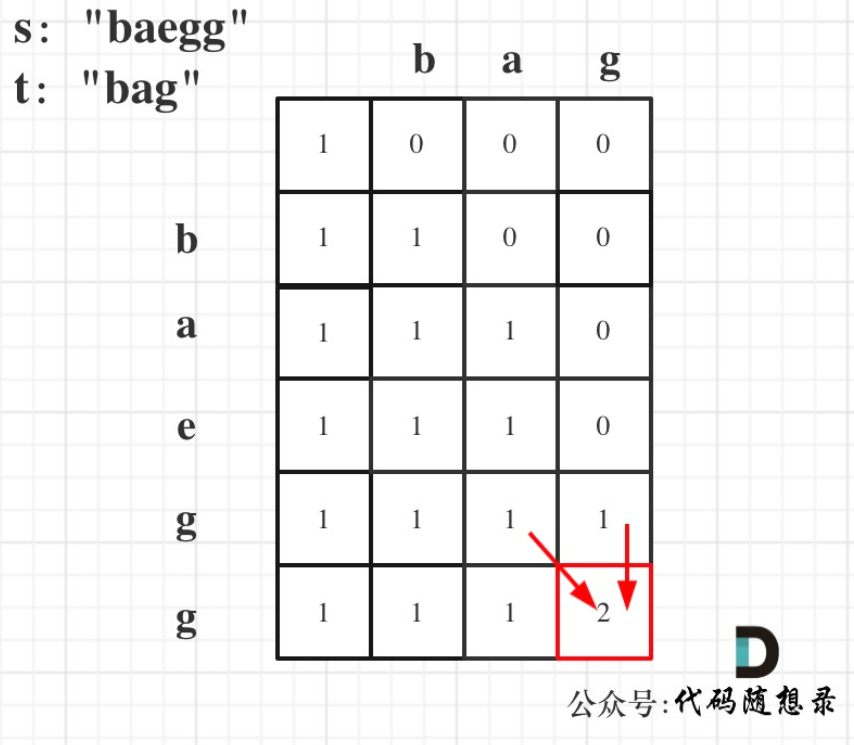
dp[i][j]：以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。（注意上个题目中我们的dp数组含义是匹配子串长度）

确定递推公式（这个部分的理解是相对之前题目困难的部分）

这一类问题，基本是要分析两种情况：s[i - 1] 与 t[j - 1]相等、s[i - 1] 与 t[j - 1] 不相等

当s[i - 1] 与 t[j - 1]相等时，dp[i][j]可以有两部分组成。一部分是用s[i - 1]来匹配，那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母，所以只需要 dp[i-1][j-1]。另一部分是不用s[i - 1]来匹配，个数为dp[i - 1][j]。所以当s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

当s[i - 1] 与 t[j - 1]不相等时，dp[i][j]只有一部分组成。不用s[i - 1]来匹配（就是模拟在s中删除这个元素），即：dp[i - 1][j]

所以递推公式为：dp[i][j] = dp[i - 1][j];

dp数组如何初始化（这个部分需要重点理解，涉及删除s当前字符后的匹配）

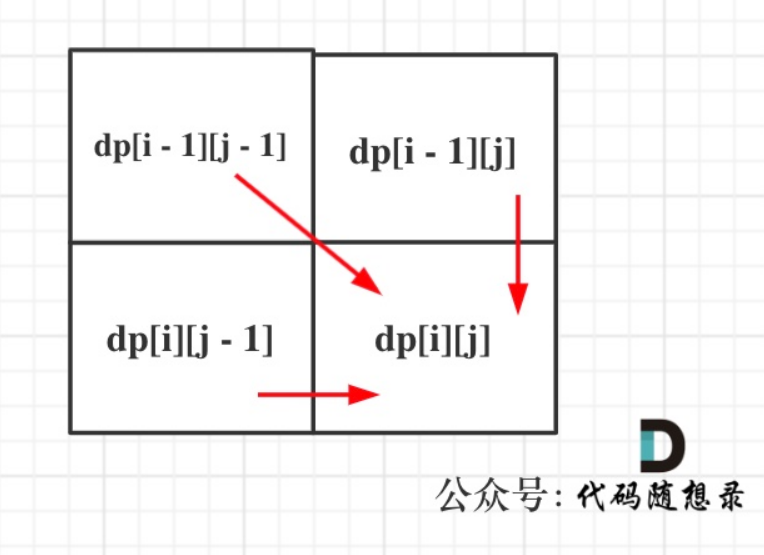
从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j] 是从上方和左上方推导而来，如图：，那么 dp[i][0] 和dp[0][j]是一定要初始化的。每次当初始化的时候，都要回顾一下dp[i][j]的定义，不要凭感觉初始化。

dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。那么dp[i][0]一定都是1，因为也就是把以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1。

dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数。那么dp[0][j]一定都是0，s如论如何也变成不了t。

最后就要看一个特殊位置了，即：dp[0][0] 应该是多少。dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t。

确定遍历顺序

从递推公式dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]; 和 dp[i][j] = dp[i - 1][j]; 中可以看出dp[i][j]都是根据左上方和正上方推出来的。

在下方模拟遍历的时候，大家可以看出来，有两个部分，一个是相同情况下，直接使用当前g，通过之前子串的重复数量来判断，另外一种是直接舍弃当前s字符串中的g，这两种情况需要大家理解清楚，这种规律很抽象，但是按照逻辑来说是正确的，需要熟悉这种动态规划的思路

class Solution:def numDistinct(self, s: str, t: str) -> int:dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]for i in range(len(s)):dp[i][0] = 1for j in range(1, len(t)):dp[0][j] = 0for i in range(1, len(s)+1):for j in range(1, len(t)+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + dp[i-1][j]else:dp[i][j] = dp[i-1][j]return dp[-1][-1]

583. 两个字符串的删除操作

动态规划一

本题和1143最长公共子序列基本一致，只要求出两个字符串的最长公共子序列长度即可，那么除了最长公共子序列之外的字符都是必须删除的，最后用两个字符串的总长度减去两个最长公共子序列的长度就是删除的最少步数。

算法训练营day44 动态规划⑪ 1143.最长公共子序列、1035.不相交的线、53. 最大子序和、392.判断子序列-CSDN博客

class Solution(object):def minDistance(self, word1, word2):m, n = len(word1), len(word2)# dp 求解两字符串最长公共子序列dp = [[0] * (n+1) for _ in range(m+1)]for i in range(1, m+1):for j in range(1, n+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = max(dp[i-1][j], dp[i][j-1])# 删去最长公共子序列以外元素return m + n - 2 * dp[-1][-1]

动态规划二

本题经过上题的铺垫之后，基本逻辑是一致的

确定dp数组（dp table）以及下标的含义

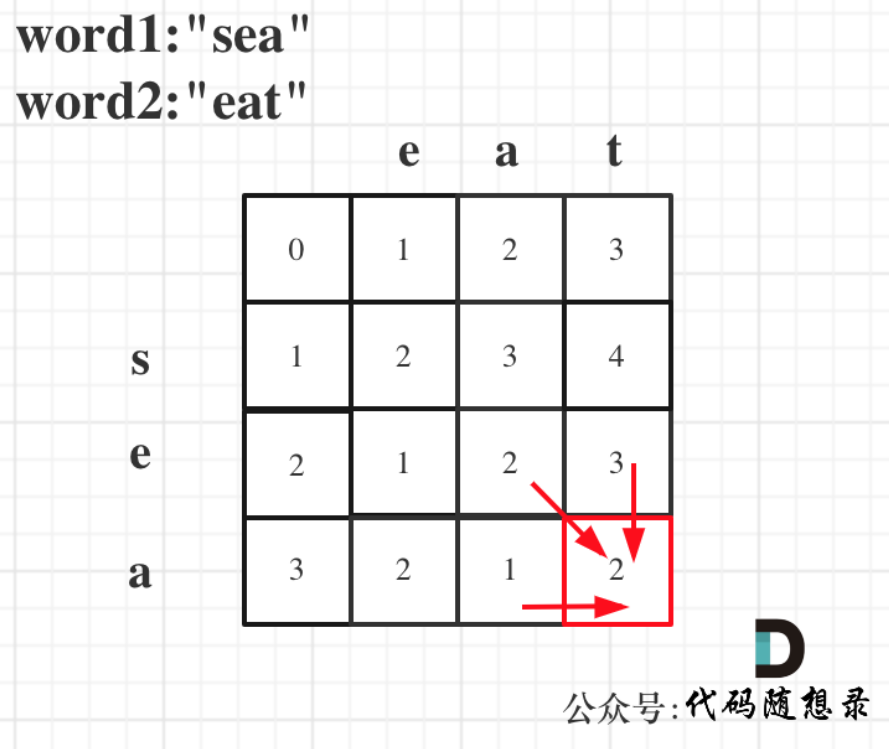
dp[i][j]：以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最少次数。

这里dp数组的定义需要重点理解！

确定递推公式

当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：

情况一：删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1
情况二：删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1
情况三：同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2

那最后当然是取最小值，所以当word1[i - 1] 与 word2[j - 1]不相同的时候，递推公式：dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});

初始化

略

遍历顺序

略

class Solution:def minDistance(self, word1: str, word2: str) -> int:dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]for i in range(len(word1)+1):dp[i][0] = ifor j in range(len(word2)+1):dp[0][j] = jfor i in range(1, len(word1)+1):for j in range(1, len(word2)+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:dp[i][j] = min(dp[i-1][j-1] + 2, dp[i-1][j] + 1, dp[i][j-1] + 1)return dp[-1][-1]

72. 编辑距离

之前的题目都是在为编辑距离做铺垫，现在终于来到了这个题目

确定dp数组（dp table）以及下标的含义

dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。

确定递推公式

以if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑，dp[i][j] 就应该是 dp[i - 1][j - 1]，即dp[i][j] = dp[i - 1][j - 1];

if (word1[i - 1] != word2[j - 1])，此时就需要编辑了

操作一：word1删除一个元素，那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离再加上一个操作。

即 dp[i][j] = dp[i - 1][j] + 1;

操作二：word2删除一个元素，那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离再加上一个操作。

即 dp[i][j] = dp[i][j - 1] + 1;

操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增删加元素。

即 dp[i][j] = dp[i - 1][j - 1] + 1;

综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

dp数组如何初始化

dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;同理dp[0][j] = j;

确定遍历顺序

class Solution:def minDistance(self, word1: str, word2: str) -> int:dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]for i in range(len(word1)+1):dp[i][0] = ifor j in range(len(word2)+1):dp[0][j] = jfor i in range(1, len(word1)+1):for j in range(1, len(word2)+1):if word1[i-1] == word2[j-1]:dp[i][j] = dp[i-1][j-1]else:dp[i][j] = min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1]) + 1return dp[-1][-1]