当前位置： 首页 > news >正文

数学建模——灰色预测（GM11）

news 2025/8/12 6:40:16

灰色理论前面灰色关联分析说过了，这里直接正题

哪些数据适合灰色预测？

1.数据量很少的

例如只告诉了长江近5年的水质情况要求预测明年的水质情况

2.需要预测的量少的

只是预测明年的水质情况而不是后面10年的

3.数据规律不明显的

1.起伏不大型2.数据存在特殊点

灰色预测原理

通过累加制造规律构建

假设原序列是x^{(0)},新的累C

那么只要我找到了新的累加序列的函数表达式那就可以反推原序列了

比如我求出来了x^{(1)}(k+1)

x^{(0)}(k+1)=x^{(1)}(k+1)-x^{(1)}(k)就可以算预测值

因此现在目标就   不是求原序列拟合函数表达式 ——>  而是求新的累加序列的拟合函数表达式

这种拟合线长得一般像指数曲线或直线

所以构建一阶常微分方程来求解拟合曲线的函数表达式

设x^{(1)}满足

\frac{dx^{(1)}}{dt}+ax^{(1)}=u

已知a和u即可求出函数表达式

再理一下逻辑：要预测x^{(0)}就得求x^{(1)}，要预测x^{(1)}就得算x^{(1)}的函数表达式，要解出函数表达式就得算微分方程，要算微分方程就得知道a和u

计算公式参考微分方程的不同形式对应的方法概括(纯公式无证明)-CSDN博客

但是带入不同的x^{(1)}会求出很多a和u，所以要使用最小二乘法，通过最小化误差的平方和找最佳匹配函数

但是数据是离散的，所以\frac{dx^{(1)}}{dt}要写成\frac{\Delta x^{(1)}}{\Delta t}，

而对于\Delta x^{(1)}，\Delta x^{(1)}=x^{(1)}(t)-x^{(1)}(t-1)=x^{(0)}(t)

   对于\Delta t     ，\Delta t=t-(t-1)=1

所以\frac{dx^{(1)}}{dt}=\frac{\Delta x^{(1)}}{\Delta t}=\frac{x^{(0)}(t)}{1}=x^{(0)}(t)

因此\frac{dx^{(1)}}{dt}+ax^{(1)}=u\Leftrightarrow x^{(0)}(t)+ax^{(1)}(t)=u\Leftrightarrow x^{(0)}(t)=u-ax^{(1)}(t)

不妨把x^{(0)}(t)看成Y，x^{(1)}(t)看成X，得到Y=u-aX

这里求解方法参考：利用regress函数即可算出两个参数（算出的X前面的参数是-a的值）

数学建模——回归分析-CSDN博客

为了更能体现前后数据的关系，把x^{(1)}(t)变成取前后两个数均值更合理

记作：z^{(1)}(t)=\frac{x^{(1)}(t)+x^{(1)}(t-1)}{2}

方程改写为x^{(0)}(t)=u-az^{(1)}(t)

这里有一个问题：左边有k个数据，右边有k-1个数据，少了一个怎么对应

其实实际上我们是舍弃了初始数据的第一个数据

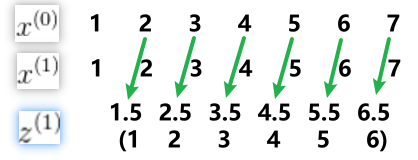
计算出au之后就计算\frac{dx^{(1)}}{dt}+ax^{(1)}=u

带入公式：

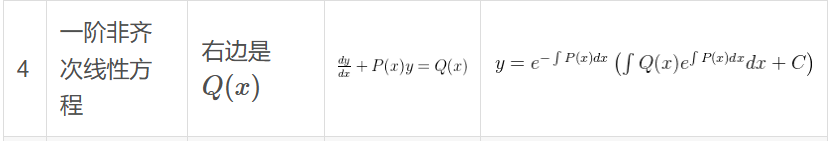
其中P(x)=a,Q(x)=u注意这里x是因变量，t才是自变量

x^{(1)}(t)=e^{-\int adt}(\int ue^{\int adt}dt+C)=e^{-at}(\int ue^{at}dt+C)=e^{-at}(\frac{u}{a}e^{at}+C)=\frac{u}{a}+Ce^{-at}

由于当t=1时x^{(1)}(1)=\frac{u}{a}+Ce^{-a}

因此C=(x^{(1)}(1)-\frac{u}{a})*e^{a}，因为x^{(1)}(1)=x^{(0)}(1)，C=(x^{(0)}(1)-\frac{u}{a})*e^{a}

x^{(1)}(t)=\frac{u}{a}+(x^{(0)}(1)-\frac{u}{a})\cdot e^{a}\cdot e^{-at}=\frac{u}{a}+(x^{(0)}(1)-\frac{u}{a})\cdot e^{-at+a}=\frac{u}{a}+(x^{(0)}(1)-\frac{u}{a})\cdot e^{-a(t-1)},t=1,2,\cdots

令k=t-1,t=k+1

因此x^{(1)}(k+1)=\frac{u}{a}+(x^{(0)}(1)-\frac{u}{a})e^{-ak},k=0,1,\cdots

数据与模型检验：

建模开始之前：

要通过级比检验判断是否适合GM（1，1）

计算\lambda (k)=\frac{x^{(0)}(k-1)}{x^{(0)}(k)},k=2,3,\cdots,n.

如果\lambda (k)在区间(e^{-\frac{2}{n+1}},e^{-\frac{2}{n+2}})，说明可以用这个模型

如果不在区间内可以给每个数据都加上一个常数，看看是否在区间内，后面计算时减去常数即可

完成建模后：

需进行残差检验

\epsilon (k)=\frac{x^{(0)}(k)-\hat{x}^{(0)}(k)}{x^{(0)}(k)},k=1,2,\cdots,n

如果\epsilon (k)<0.2认为模型可以预测

也可以加入级比检验

如果没有通过就得考虑换一个模型了

整体流程

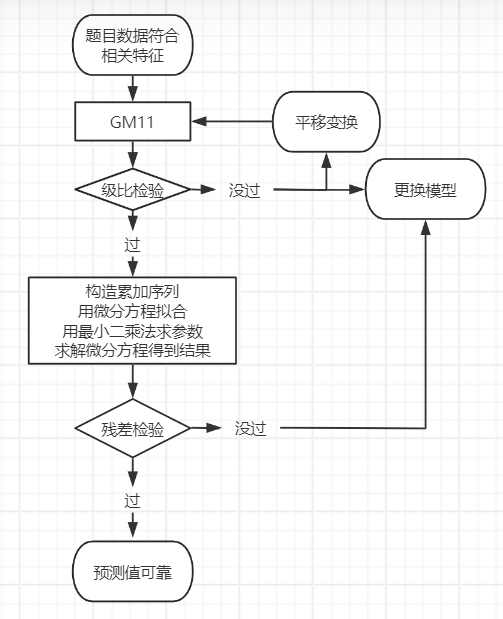
参考视频

http://www.dtcms.com/a/325648.html

相关文章：

  • YOLO性能评估指标详细总结
  • Linux中DHCP配置指南指南（配实验步骤与注释）
  • 19.Linux DHCP服务
  • 108-基于Python的中国古诗词数据可视化分析系统
  • 第二章：变量与简单数据类型
  • JVM管理数据的方式
  • 深入解析Prompt缓存机制：原理、优化与最佳实践
  • k8s之CSI 卷挂载问题：同一Pod中挂载多个相同远程存储的隐含限制
  • 2025面试题——（12）
  • Vue3从入门到精通：3.1 性能优化策略深度解析
  • 思科交换机的不同级别IOS软件有什么区别？
  • android 换肤框架详解1-换肤逻辑基本
  • R语言机器学习算法实战系列（二十七）LASSO 与 Adaptive LASSO 在特征选择中的比较与应用
  • 为什么TEXT不区分大小写，而BLOB严格区分？
  • 剑桥大学最新研究：基于大语言模型(LLM)的分子动力学模拟框架，是MD的GPT时刻还是概念包装？
  • Selenium竞品价格监控爬虫（代理防封版）
  • C语言模拟 MCU 上电后程序的执行顺序 + 回调函数机制 + 程序计数器（PC）和堆栈的作用
  • PID 控制算法 | stm32 直流电机控制
  • 从零开始的云计算生活——项目实战容器化
  • 当生产环境卡成 PPT：Spring Boot 线程 Dump 捉妖指南 - 第544篇
  • AI入门学习--如何写好prompt？
  • STM32学习笔记7-TIM输入捕获模式
  • 1000w小时语音数据！语音模型Higgs Audio V2情感能力跃迁；MathCaptcha10k提升验证码识别技术
  • 主DNS部署+辅助DNS服务器部署
  • 嵌入式学习（Day24）fread/fwrite
  • 【华为机试】208. 实现 Trie (前缀树)
  • 钓鱼鱼饵制作的方式
  • 【项目测试】：问卷考试系统项目测试报告
  • FlinkSql（详细讲解一）
  • C#中如何运用JWT用户认证