二叉树进阶 之 【二叉搜索树的简介与模拟实现的前提准备】
目录
1.二叉搜索树的概念
2.实现的前提准备
1.二叉搜索树的概念
二叉搜索树又称二叉查找树或二叉排序树
它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
二叉搜索树是递归定义的,最小子问题是空树
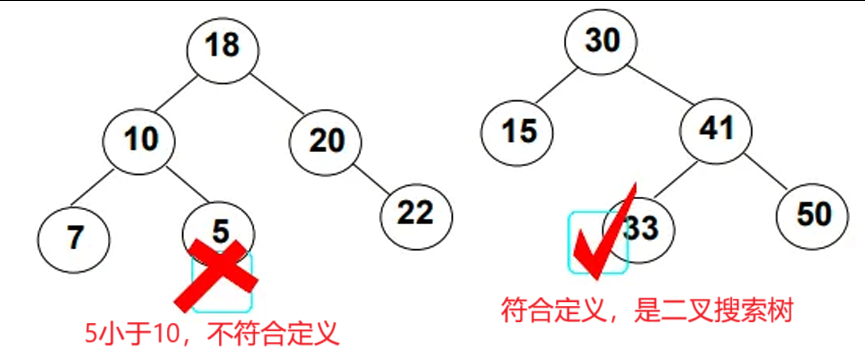
二叉搜索树主要有查找、插入、删除的功能,并且二叉树的中序遍历正好是数据的有序遍历
2.实现的前提准备
(1)文件与命名空间
创建一个BinarySearchTree.h文件来保存模拟实现的二叉搜索树
为了避免命名冲突,创建一个新的命名空间来封装模拟实现的二叉搜索树
(2)分类
与list实现相似,二叉搜索树实现需要两个类,
一个类管理单个树节点的定义、初始化等操作
另一个类管理不同树节点间的链接关系,继而实现相应功能
namespace dfq
{//管理单个的树节点template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};//管理不同的树节点template<class K>class BSTree{typedef BSTreeNode<K> Node;private:Node* _root;};
}(1)通常将二叉搜索树节点的存储值叫作value,通过键值(key)的比较决定节点位置
从而有 K模型 与 KV模型 的说法,这里我们先讨论 K模型
(2)后续需频繁使用树节点,使用 struct 定义管理单个树节点的类
(3)树节点中需保存左右孩子指针及键值,再手写构造函数进行初始化
(4)只需要根节点就可以管理不同树节点间的链接关系
(3)默认成员函数
//构造函数
BSTree():_root(nullptr)
{ }//拷贝构造
BSTree(const BSTree<K>& t)
{//改变根节点_root = Copy(t._root);
}Node* Copy(Node* root)
{if (!root)return nullptr;Node* copyroot = new Node(root->_key);copyroot->_left = Copy(root->_left);copyroot->_right = Copy(root->_right);return copyroot;
}(1)拷贝构造创建的树只是树节点键值、连接关系与传入对象相同,为防止内存的重复释放需要进行深拷贝
(1)拷贝构造的重点是递归的使用(使用前序遍历,访问当前树的根节点时即进行拷贝操作)
(2)另起一个Copy函数,最小子问题是空树,
如果根节点为空,返回值为nullptr,否则,
先创建一个新的树节点拷贝当前树的根节点的键值,
再递归调用函数完成不同节点间的链接关系

当递归到空树时,函数开始返回,不同树节点的链接开始....
//析构函数
~BSTree()
{//传入根节点,后续遍历删除Destroy(_root);
}void Destroy(Node*& root)
{if (!root)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;
}(1)使用后序遍历的思想(减少临时保存的操作)销毁一棵二叉搜索树
因为析构函数不能传参,这里调用子函数进行销毁
(2)传入节点指针的引用,可在销毁树节点的同时置空该指针
(3)最小子问题是空树,树为空就返回,否则
先销毁左子树,再销毁右子树,最后销毁根节点
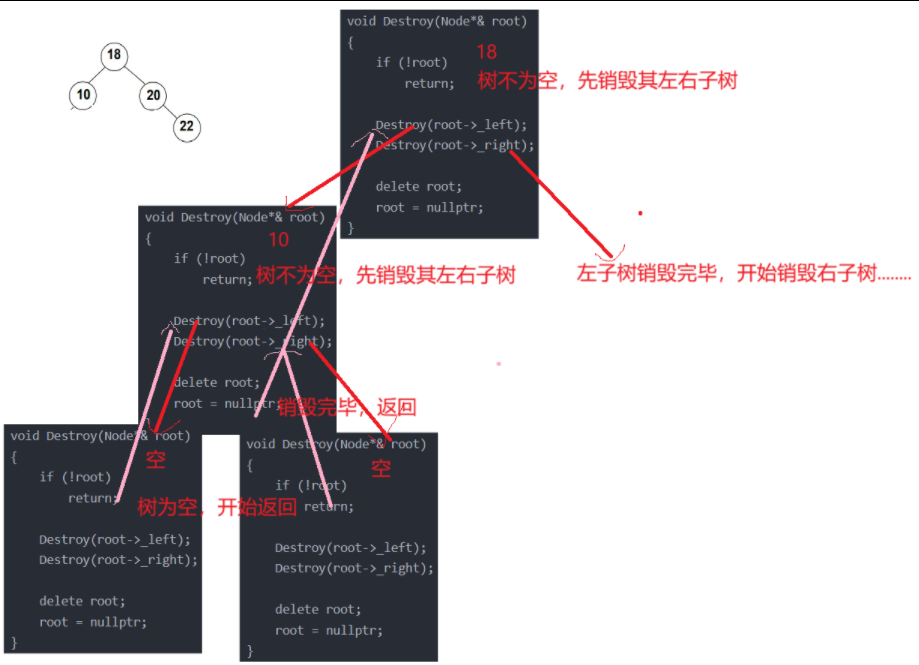
(1)红色的线代表向下递归,直到树为空时开始自底向上销毁
//复制重载
BSTree<K, V>& operator=(BSTree<K, V> t)
{swap(_root, t._root);return *this;
}赋值重载的简洁之处在于,传值传参就可完成深拷贝(默认拷贝构造正确实现)
此时只需交换两棵树的根节点即可
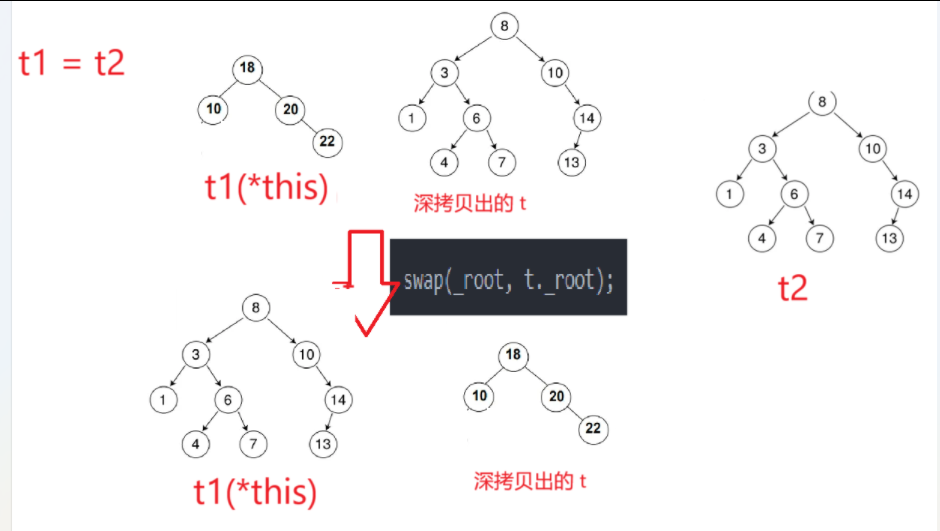
知道了一棵二叉搜索树的根节点,“树藤摸瓜”,即可访问整棵树,
所以我们可以说,根节点就是一棵树的代表
我们使用根节点管理一棵树,那么交换两棵树的根节点就是在交换两棵树
