算法训练之队列和优先级队列

---

♥♥♥~~~~~~欢迎光临知星小度博客空间~~~~~~♥♥♥

♥♥♥零星地变得优秀~也能拼凑出星河~♥♥♥

♥♥♥我们一起努力成为更好的自己~♥♥♥

♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥

♥♥♥如果有什么问题可以评论区留言或者私信我哦~♥♥♥

✨✨✨✨✨✨个人主页✨✨✨✨✨✨

---

        这一篇博客我们来研究研究队列和优先级队列相关的算法练习题，准备好了吗~我们发车去探索算法的奥秘啦~🚗🚗🚗🚗🚗🚗

目录

前言😍

队列（Queue）😊

1. 定义

2. 基本操作

3. 实现方式

优先级队列（Priority Queue）😀

1. 定义

2. 核心特性

3. 基本操作

4. 实现方式

N叉树的层序遍历🐷

二叉树的锯齿形层序遍历😁

二叉树的最大宽度😜

最后一块石头的重量😀

数据流中第K大的元素🤨

前K个高频单词👍

数据流的中位数😜

---

前言😍

        队列和优先级队列都有队列两个字，是不是差不多呢？别急，我们一起来看看~

队列（Queue）😊

1. 定义

        队列是一种先进先出（FIFO, First In First Out）的线性数据结构，即最早进入队列的元素会最先被移除。类似于现实中的排队场景（如超市结账、公交车上车），先到的人先处理，后到的人后处理。

2. 基本操作

具体操作可以参考cplusplus上面的queue容器C++——queue

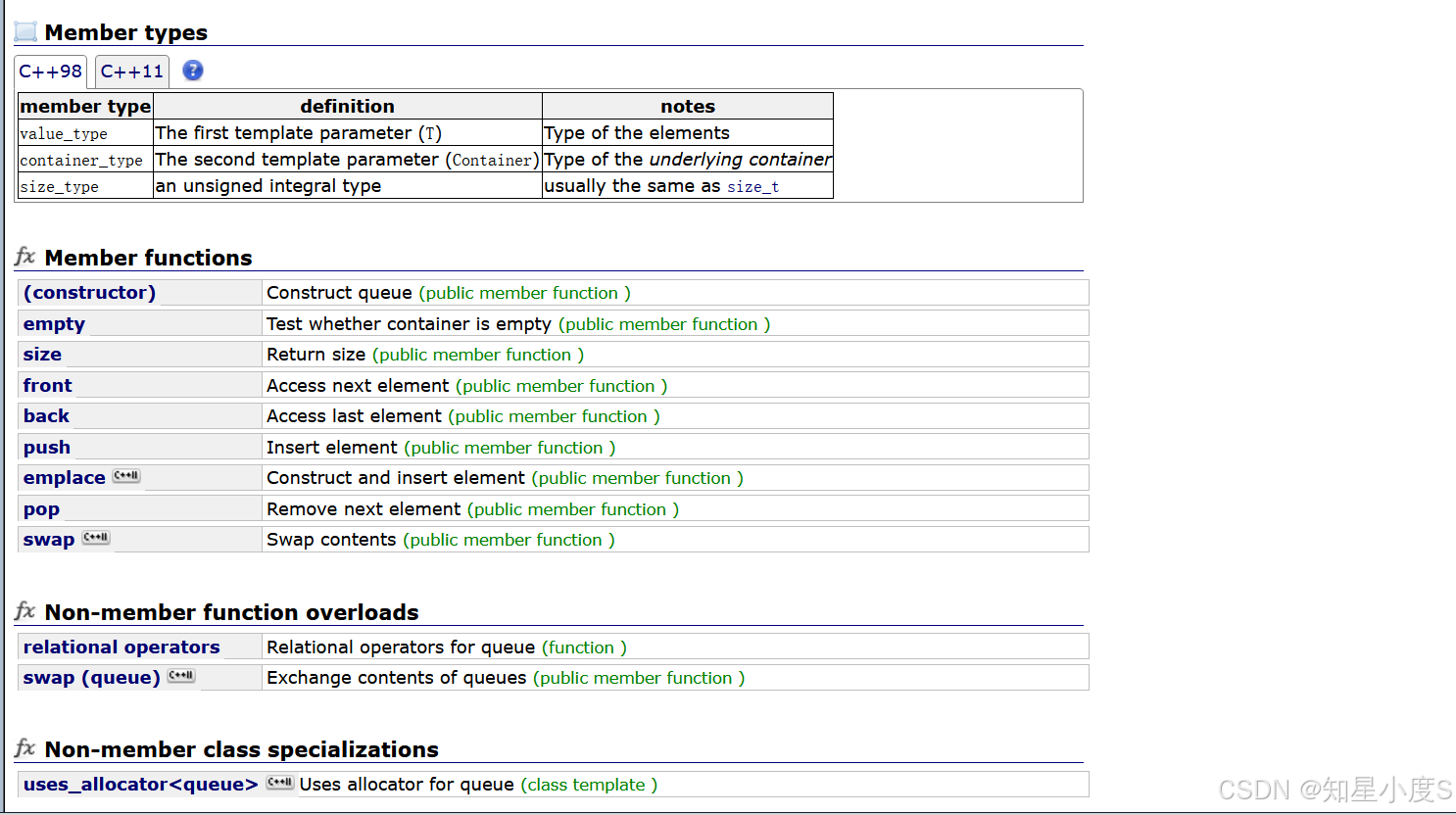
队列的核心操作包括：

• 入队（Enqueue）：将元素添加到队列的尾部（“队尾”）。
• 出队（Dequeue）：移除并返回队列头部的元素（“队首”）。
• 查看队首（Front）：获取队首元素（不移除）。
• 判断空（IsEmpty）：检查队列是否为空。

3. 实现方式

队列可通过多种方式实现，常见方式有：

• 顺序存储（数组）：用数组存储元素，通过“头指针”和“尾指针”标记队首和队尾。需处理数组扩容问题（当队列满时动态扩展数组）。
• 链式存储（链表）：用单链表实现，队首为链表头节点，队尾为链表尾节点。入队在尾节点添加，出队在头节点删除，无需处理扩容，但需要维护尾指针。

优先级队列（Priority Queue）😀

1. 定义

        优先级队列是一种出队顺序由元素的优先级决定的队列，优先级最高的元素最先出队（而非按到达顺序）。类似于现实中的“插队”场景（如医院急诊，病情严重的患者优先处理）。

2. 核心特性

• 每个元素有一个关联的“优先级”（通常用数值表示，如数值越大优先级越高，或越小越高）。
• 出队时，优先级最高的元素被移除；若多个元素优先级相同，则按到达顺序（或自定义规则）处理。

3. 基本操作

具体操作可以参考cplusplus上面的priority_queue容器C++——priority_queue

优先级队列的核心操作与普通队列类似，但出队规则不同：

• 入队（Enqueue）：将元素按优先级插入合适的位置（或插入队尾，再调整位置）。
• 出队（Dequeue）：移除并返回优先级最高的元素。
• 查看最高优先级（Top/Peek）：获取当前优先级最高的元素（不移除）。

4. 实现方式

优先级队列的关键是高效地获取和调整优先级，常见实现方式为堆（Heap），尤其是二叉堆（最大堆或最小堆）：

• 大根堆：父节点的优先级高于子节点，堆顶是优先级最高的元素（出队时直接取堆顶）。
• 小根堆：父节点的优先级低于子节点，堆顶是优先级最低的元素（需调整为最大堆逻辑）。

其他实现方式（效率较低）：

• 无序数组：入队时直接插入队尾，出队时遍历数组找到最高优先级元素（时间复杂度 O(n)）。
• 有序数组：入队时按优先级插入合适位置（O(n)），出队时取队首（O(1)）。

N叉树的层序遍历🐷

N叉树的层序遍历

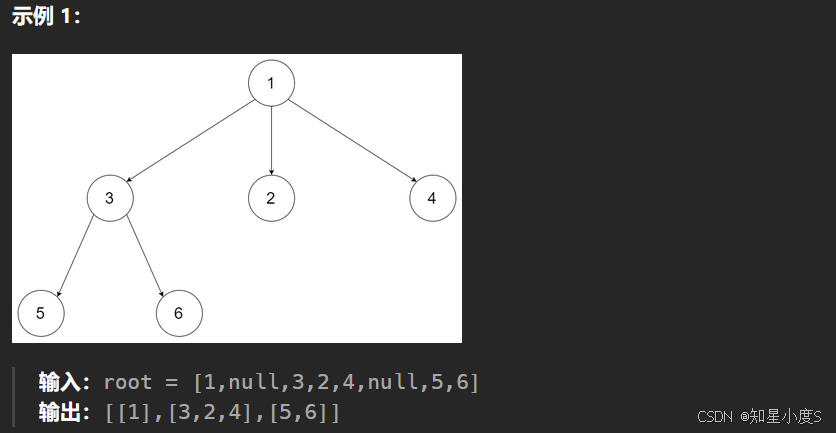
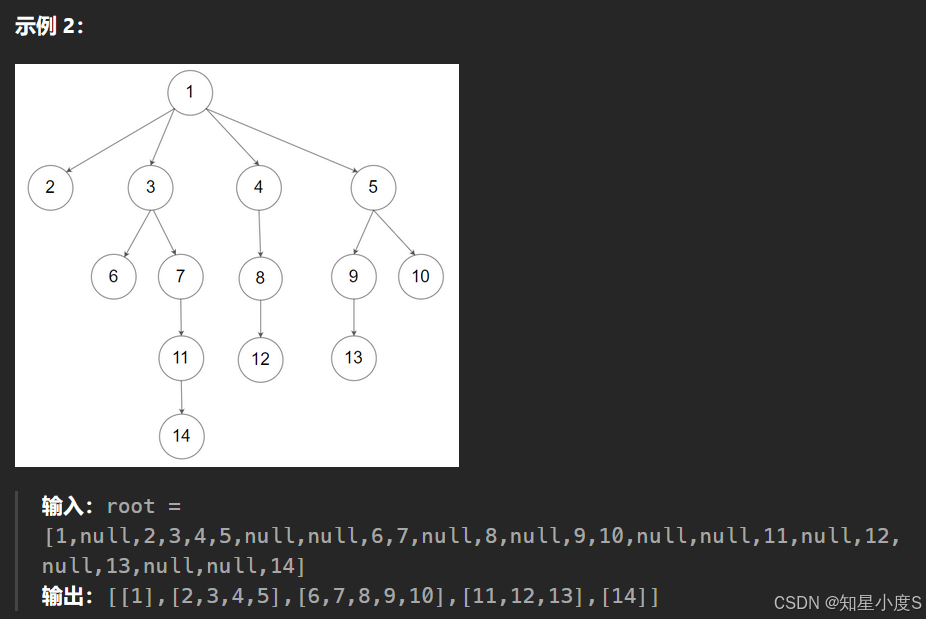
        层序遍历相信大家以前也接触过，就像波浪一层层向外面扩散，我们需要借助队列来完成这一个题目~

算法思路：辅助队列来帮忙

①创建辅助队列，处理边界情况（根结点为空）

②头结点入队列，记录当前层数

③分层处理（变量添加记录当前层个数），记录结果，当前层结点出队列，不为空的孩子结点入队列

④返回结果

代码实现：

//N叉树的层序遍历
/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution
{
public:vector<vector<int>> levelOrder(Node* root){//1、创建辅助队列queue<Node*> q;vector<vector<int>> ret;//保存结果//处理边界情况if (root == nullptr){return ret;//返回空数组}//2、根结点入队列q.push(root);//3、处理每一层while (!q.empty()){int n = q.size();//队列元素个数就是当前层元素个数vector<int> tmp;//记录当前层数据结果for (int i = 0; i < n; i++)//当前层结点出队列，让它们的孩子入队列//队头——出队列，队尾——入队列{Node* t = q.front();q.pop();tmp.push_back(t->val);//进入当前结点数据数组for (auto& e : t->children){if (e)q.push(e);//孩子不为空入队列}}//记录结果ret.push_back(tmp);}//4、返回结果return ret;}
};

顺利通过~

二叉树的锯齿形层序遍历😁

二叉树的锯齿形层序遍历

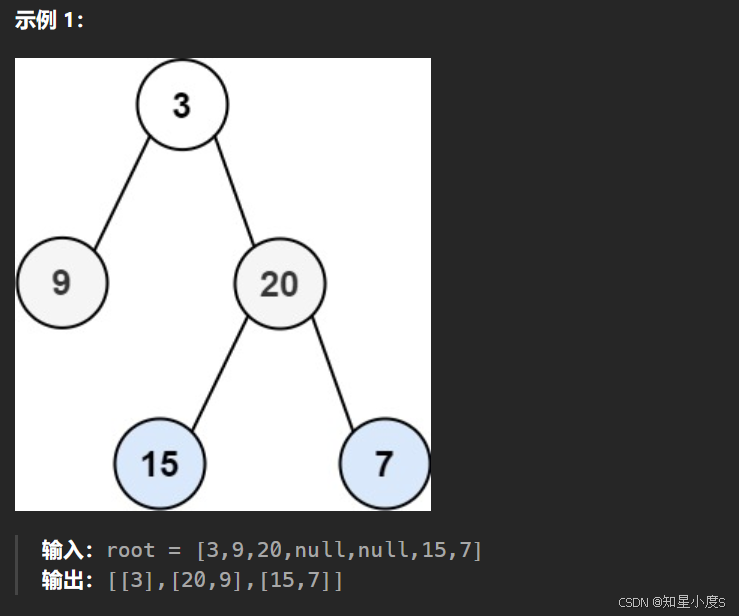
        这一个题目和前面那一个题目是类似的，并且还是我们熟悉的二叉树，但是它的层序遍历是锯齿形的也就是S/Z形~

算法思路：辅助队列+增加变量法

        辅助队列就不用多说，我们只需要添加一个变量看看当前层是奇数/偶数层，偶数层当前层逆序保存,奇数层直接保存~

代码实现：

//二叉树的锯齿形层序遍历
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution
{
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root){//1、创建辅助队列queue<TreeNode*> q;vector<vector<int>> ret;//记录结果//处理边界情况if (root == nullptr){return ret;//返回空数组}//2、头结点入队列，记录当前层数q.push(root);int layer = 1;//3、分层处理，记录结果while (!q.empty()){int n = q.size();//当前层结点数vector<int> tmp;//记录当前层数据//当前层结点出队列，不为空的孩子结点入队列for (int i = 0; i < n; i++){TreeNode* t = q.front();q.pop();tmp.push_back(t->val);if (t->left)q.push(t->left);if (t->right)q.push(t->right);}//偶数层当前层逆序保存,奇数层直接保存if (layer % 2 == 0)reverse(tmp.begin(), tmp.end());ret.push_back(tmp);//层数++layer++;}//4、返回结果return ret;}
};

顺利通过~

二叉树的最大宽度😜

二叉树的最大宽度

 

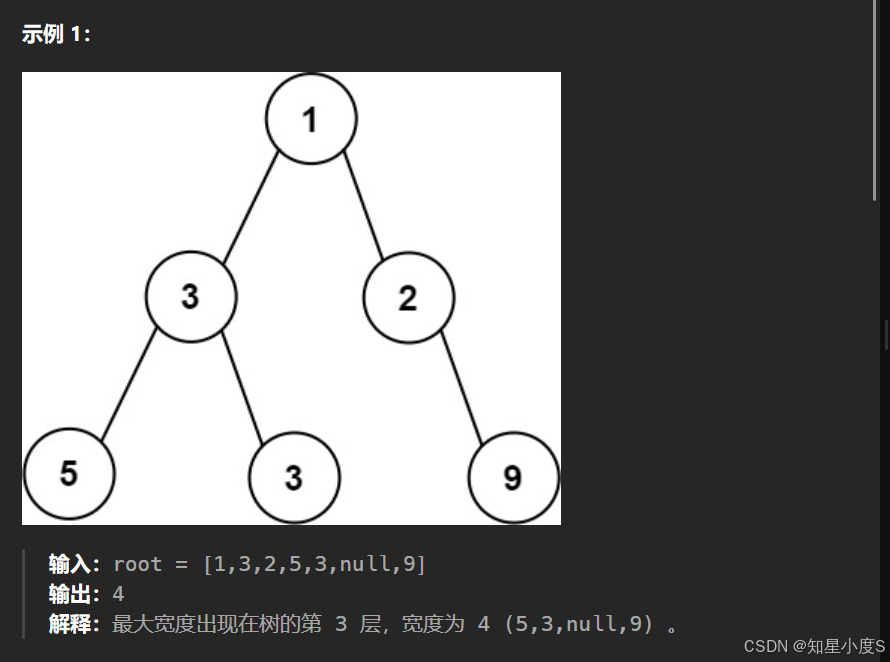
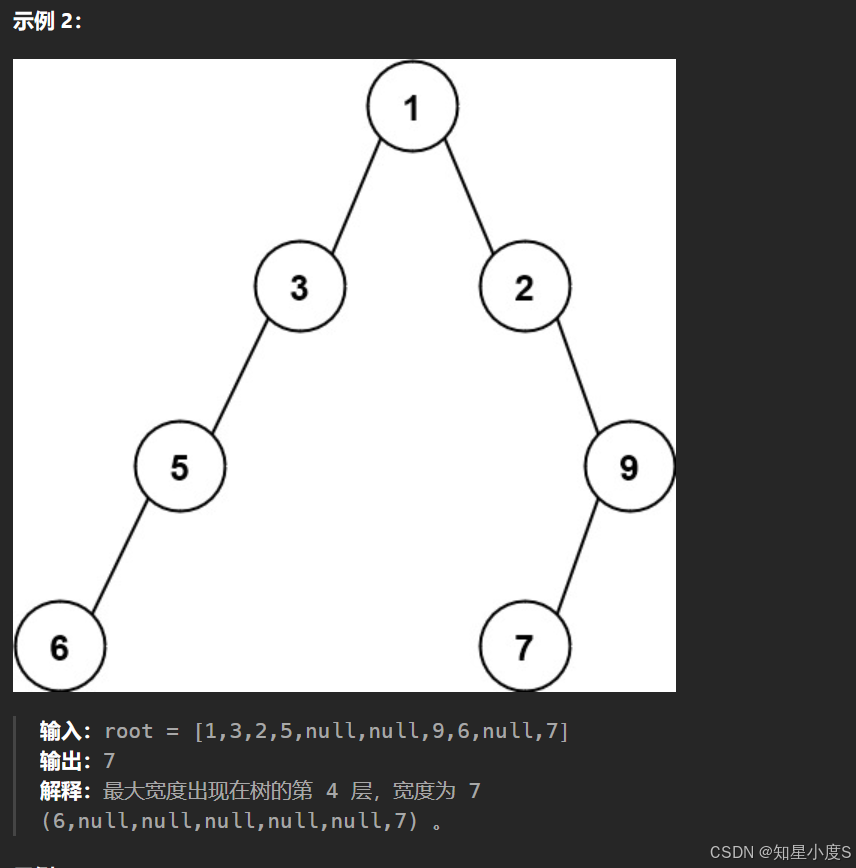
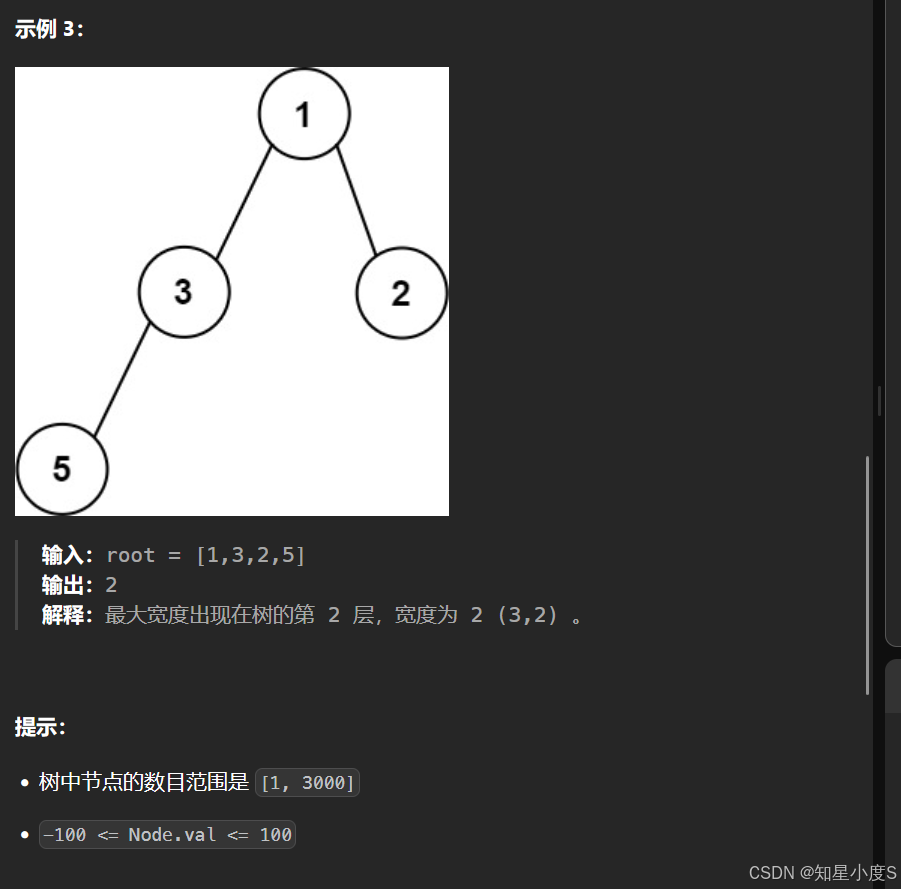
        题目要求二叉树的最大宽度，还跟我们平时求的二叉树最大宽度不一样，还包括了中间的空指针~这就需要我们进行优化了~

算法思路：模拟数组保存结点的思想

①节点编号：将二叉树视为完全二叉树结构进行编号    

根节点编号为 1，对于编号为 i 的节点，其左子节点编号为 2*i，右子节点编号为 2*i + 1。

②层序遍历：使用队列进行BFS，队列元素为 pair<TreeNode*, unsigned int>（节点指针 + 节点编号）

③逐层计算宽度：

在每层遍历时：当前层宽度 = 队尾节点编号 - 队首节点编号 + 1；更新全局最大宽度 ret

④处理子节点：将当前层节点的非空子节点及其编号加入队列

代码实现：

//二叉树的最大宽度
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution
{
public:int widthOfBinaryTree(TreeNode* root){//把二叉树看作数组保存——结点与下标联系起来//起始结点下标为1//根结点下标为i，左孩子结点下标为2*i，右孩子结点下标为2*i+1queue<pair<TreeNode*, unsigned int>> q;unsigned int ret = 0;//记录最大宽度//处理边界情况if (root == nullptr){return ret;}//头结点入队列q.push({ root,1 });while (q.size()){//更新结果auto& [x1, y1] = q.front();auto& [x2, y2] = q.back();ret = max(ret, y2 - y1 + 1);//当前层头尾结点下标差值+1就是结果int n = q.size();//当前层结点出队列，当前层结点的非空孩子结点入队列for (int i = 0; i < n; i++){auto& [x, y] = q.front();if (x->left)q.push({ x->left,y * 2 });if (x->right)q.push({ x->right,y * 2 + 1 });q.pop();}}//返回结果return ret;}
};

顺利通过~

最后一块石头的重量😀

最后一块石头的重量

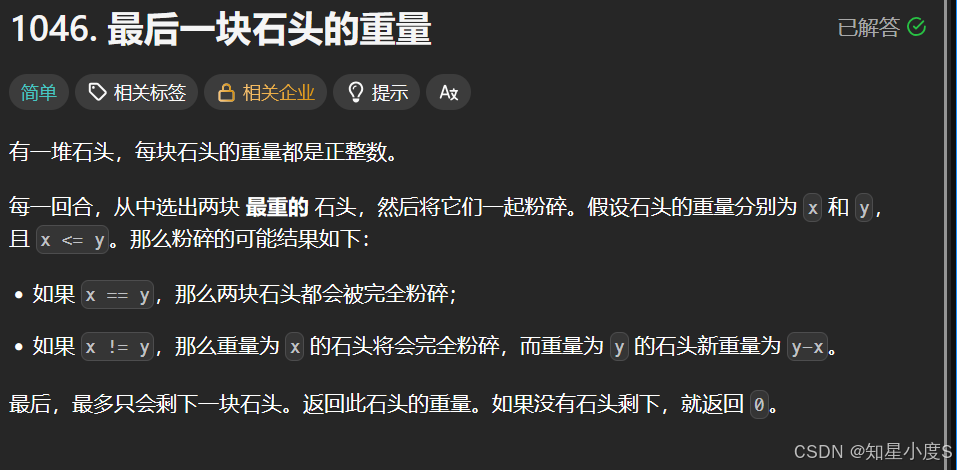
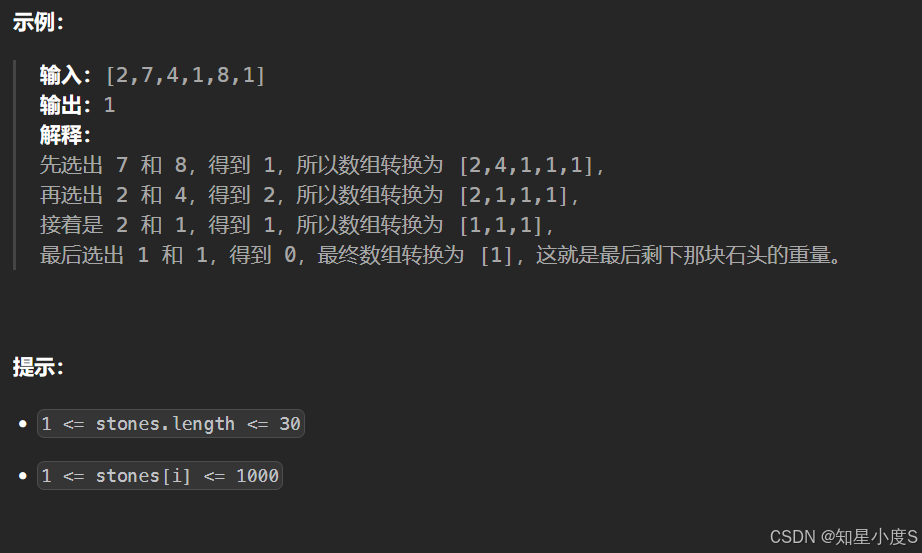
        我们可以看到需要重复取最大的两个数进行操作，那么我们就可以使用我们的优先级队列了，创建一个大根堆进行操作~

算法思路：大根堆

①创建大根堆，C++priority_queue容器默认为大根堆

②数据所有元素入堆

③循环取堆中最大和次大两个元素进行操作，不相等插入差值，相等完全粉碎不用管

代码实现：

//最后一块石头的重量
class Solution
{
public:int lastStoneWeight(vector<int>& stones){//1、创建大根堆priority_queue<int>  heap;//C++默认为大根堆//2、数据所有元素入堆for (auto& e : stones){heap.push(e);}//3、循环取堆中最大和次大两个元素进行操作//直到一块石头或者没有石头while (heap.size() > 1){int a = heap.top();//最大元素heap.pop();int b = heap.top();////次大元素heap.pop();if (a != b)heap.push(a - b);//不相等插入差值//相等完全粉碎}//4、返回结果if (heap.size())return heap.top();return 0;}
};

顺利通过~

数据流中第K大的元素🤨

数据流中第K大的元素

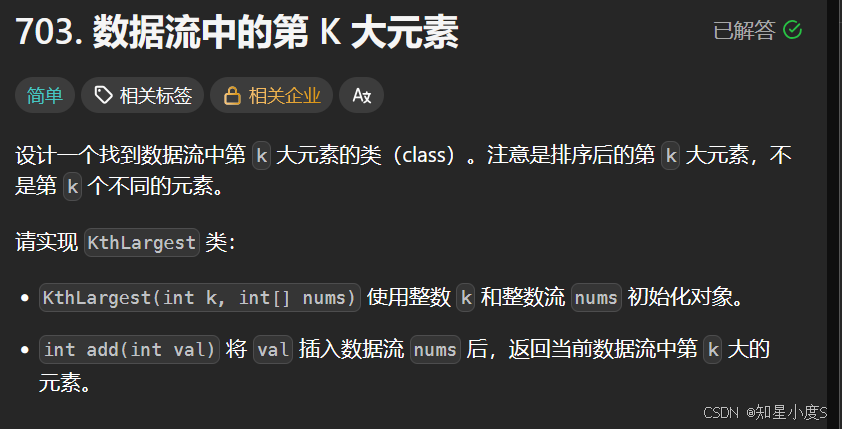
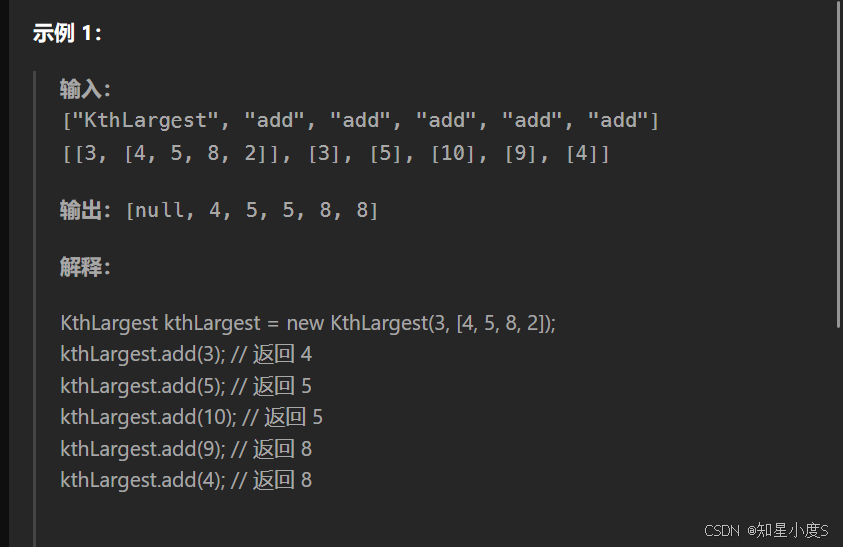
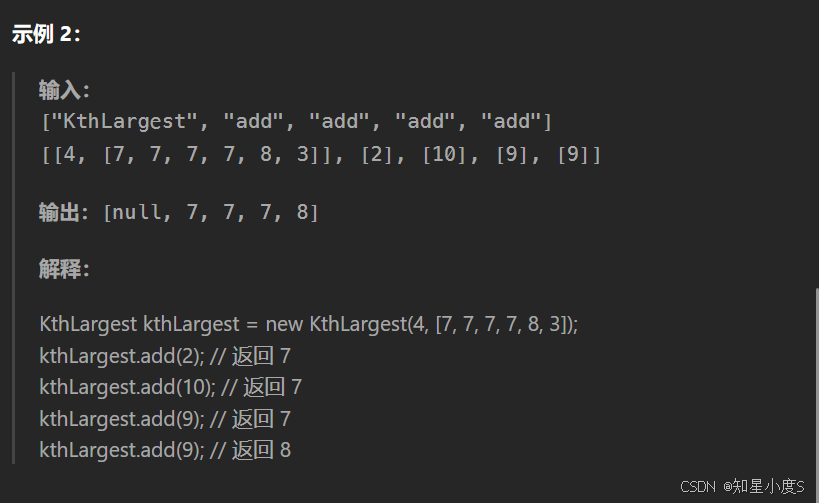
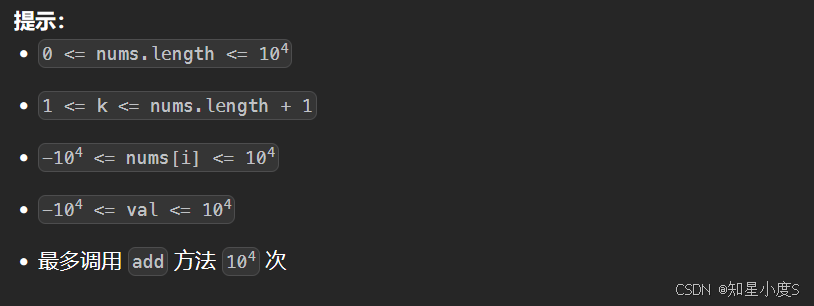
        这个总体思路是希望我们求第K大的元素，并且完成初始化，我们同样可以使用堆来解决问题，求第K大的元素那么我们可以创建小根堆，同时控制堆大小小于等于k~

算法思路：小根堆

        创建小根堆，保证堆中元素个数小于等于k，栈顶元素就是第K大元素~

代码实现：

//数据流中第K大的元素
class KthLargest
{priority_queue<int, vector<int>, greater<int>> heap;//小根堆int _k;
public:KthLargest(int k, vector<int>& nums){//完成初始化_k = k;//遍历数组将所有元素加入堆for (auto& e : nums){heap.push(e);if (heap.size() > _k)heap.pop();//数据多了，就删除}}int add(int val){heap.push(val);//新数据入堆if (heap.size() > _k)heap.pop();//数据多了，就删除return heap.top();}
};/*** Your KthLargest object will be instantiated and called as such:* KthLargest* obj = new KthLargest(k, nums);* int param_1 = obj->add(val);*/

顺利通过~

前K个高频单词👍

前K个高频单词

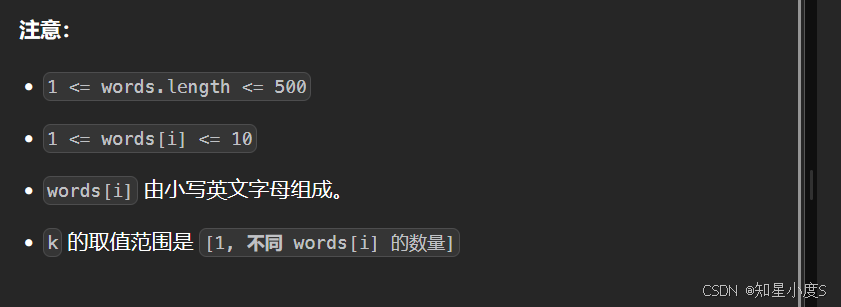
        要求我们已经知道了，求前面K个高频单词，那我们就可以就是小根堆的比较逻辑；另外还有一个要求，如果频次相同那么按照字典序（从小到大）相同，那么就是大根堆的比较逻辑，创建堆的时候我们需要自己写好比较逻辑~同时单词出现的频率我们需要创建哈希表来进行保存~

算法思路：堆（注意建堆逻辑）

①创建哈希表，保存单词频率

②创建堆，控制比较/建堆逻辑；频次相同，创建大根堆（按照字典序从小到大）；频次不相同，创建小根堆（按照频次从大到小）

③遍历哈希表，元素入堆，控制堆的大小

④使用数组记录结果，频次由大到小返回，需要逆序结果

代码实现：

//前K个高频单词
class Solution
{typedef pair<string, int> Psi;//重复使用struct cmp{bool operator()(const Psi a, const Psi b){//频次相同，创建大根堆if (a.second == b.second)return a.first < b.first;//小的沉下去//频次不相同，创建小根堆return a.second > b.second;//大的沉下去}};
public:vector<string> topKFrequent(vector<string>& words, int k){//1、创建哈希表，保存单词频率unordered_map<string, int> hash;for (auto& e : words){hash[e]++;}//2、创建堆，控制比较/建堆逻辑priority_queue<Psi, vector<Psi>, cmp> heap;//3、遍历哈希表，元素入堆for (auto& psi : hash){heap.push(psi);if (heap.size() > k)heap.pop();//如果元素个数大于k就出堆}//4、记录结果返回vector<string> ret;while (!heap.empty()){ret.push_back(heap.top().first);heap.pop();}//频次由大到小返回，需要逆序结果reverse(ret.begin(), ret.end());return ret;}
};

顺利通过~

数据流的中位数😜

数据流的中位数

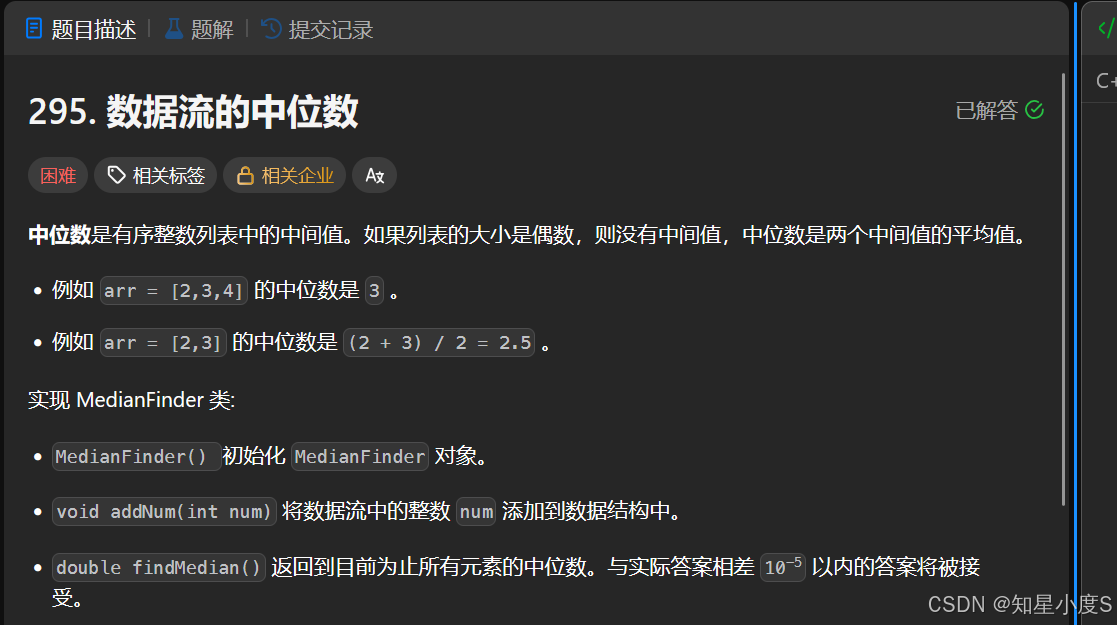
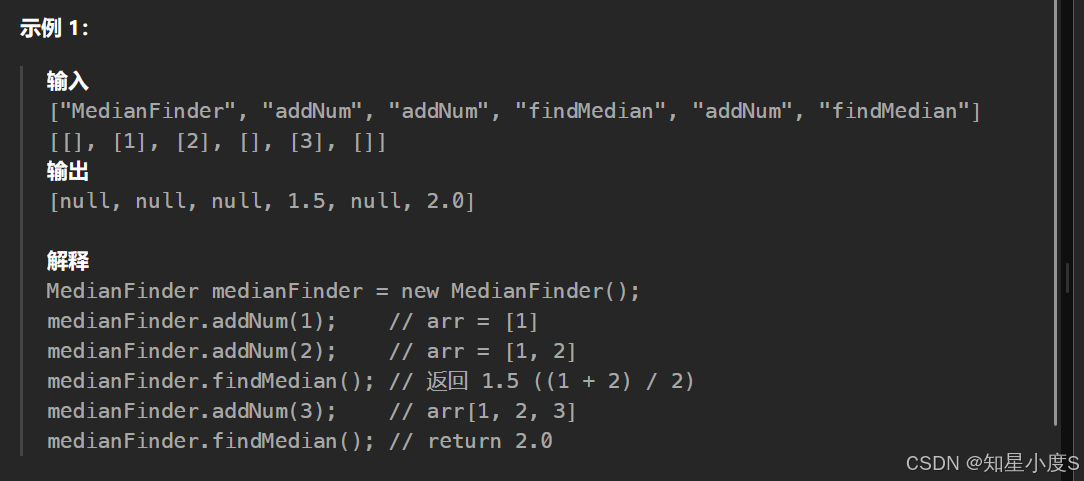
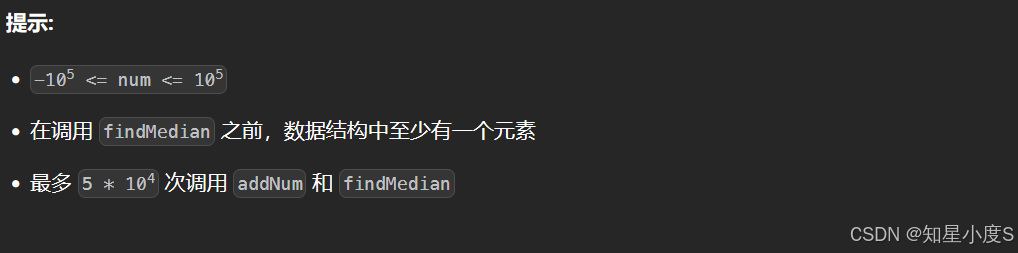
        题目要求应该比较清晰了，这个题目使用我们常规的sort排序再找中位数会超时~这里给出新方法~

算法思路：大小堆找数据流的中位数

①双堆数据结构设计

使用 大根堆（left） 存储较小一半数据，堆顶为最大值

使用 小根堆（right） 存储较大一半数据，堆顶为最小值

②动态平衡策略

• 强制约束堆大小关系：left.size() == right.size()（偶数）或 left.size() = right.size() + 1（奇数）

• 添加新数时根据当前堆状态分支处理：

  • 当两堆等大：新数≤left.top()则插入左堆，否则先插右堆再移右堆顶到左堆

  • 当左堆更大：新数≤left.top()则先插左堆再移左堆顶到右堆，否则直接插右堆

时间复杂度：O(log n)，每次最多2次堆插入/删除操作

③中位数查询机制

偶数元素：中位数 = (left.top() + right.top()) / 2.0（两堆顶均值）

奇数元素：中位数 = left.top()（左堆顶即中间值）

查询时间复杂度：O(1)，直接访问堆顶

大小堆优势：

①避免全局排序：通过堆局部有序性维护数据分区

②实时更新：每次添加自动调整堆结构保持平衡

③高效查询：中位数获取仅需常数时间，适用于数据流场景

④适应性：动态处理任意长度的输入序列

代码实现：

//数据流的中位数
class MedianFinder
{//大小堆找数据流的中位数//左边数据大根堆priority_queue<int> left;//右边数据小根堆priority_queue<int, vector<int>, greater<int>> right;
public:MedianFinder(){}//保证left.size()==right.size()//或者left.size()==right.size()+1void addNum(int num){if (left.size() == right.size()){if (left.size() == 0 || num <= left.top()){//left.size()==right.size()+1,不需要调整left.push(num);}else{right.push(num);//left.size()+1==right.size()，需要进行调整left.push(right.top());right.pop();}}else//left.size()==right.size()+1{if (num <= left.top()){left.push(num);//left.size()==right.size()+2，需要进行调整right.push(left.top());left.pop();}else{//left.size()==right.size(),不需要调整right.push(num);}}}double findMedian(){//总个数为偶数情况，中位数为中间两个数平均值if (left.size() == right.size())return (left.top() + right.top()) / 2.0;//left.size()==right.size()+1elsereturn left.top();}
};/*** Your MedianFinder object will be instantiated and called as such:* MedianFinder* obj = new MedianFinder();* obj->addNum(num);* double param_2 = obj->findMedian();*/

顺利通过~

---

♥♥♥本篇博客内容结束，期待与各位优秀程序员交流，有什么问题请私信♥♥♥

♥♥♥如果这一篇博客对你有帮助~别忘了点赞分享哦~♥♥♥

✨✨✨✨✨✨个人主页✨✨✨✨✨✨

---