当前位置：首页 > news >正文

Pytorch深度学习框架实战教程-番外篇07-Pytorch优化器详解和实战指南

news 2025/8/11 9:05:46

相关文章 + 视频教程

《Pytorch深度学习框架实战教程01》《视频教程》

《Pytorch深度学习框架实战教程02：开发环境部署》《视频教程》

《Pytorch深度学习框架实战教程03：Tensor 的创建、属性、操作与转换详解》《视频教程》

《Pytorch深度学习框架实战教程04：Pytorch数据集和数据导入器》《视频教程》

《Pytorch深度学习框架实战教程05：Pytorch构建神经网络模型》《视频教程》

《Pytorch深度学习框架实战教程06：Pytorch模型训练和评估》《视频教程》

《Pytorch深度学习框架实战教程09：模型的保存和加载》《视频教程》

《Pytorch深度学习框架实战教程10：模型推理和测试》《视频教程》

《Pytorch深度学习框架实战教程-番外篇01-卷积神经网络概念定义、工作原理和作用》

《Pytorch深度学习框架实战教程-番外篇02-Pytorch池化层概念定义、工作原理和作用》

《Pytorch深度学习框架实战教程-番外篇03-什么是激活函数，激活函数的作用和常用激活函数》

《PyTorch 深度学习框架实战教程-番外篇04：卷积层详解与实战指南》

《Pytorch深度学习框架实战教程-番外篇05-Pytorch全连接层概念定义、工作原理和作用》

《Pytorch深度学习框架实战教程-番外篇06：Pytorch损失函数原理、类型和案例》

《Pytorch深度学习框架实战教程-番外篇10-PyTorch中的nn.Linear详解》

一、什么是优化器？

优化器（Optimizer）是深度学习中用于调整模型参数（如权重、偏置）以最小化损失函数的算法。它通过分析损失函数的梯度（由反向传播计算），决定如何更新参数，最终使模型的预测误差（损失值）尽可能小。

简单来说，损失函数告诉模型 “当前预测有多差”，而优化器告诉模型 “如何调整参数才能变得更好”。

二、优化器的工作原理

优化器的核心工作流程基于梯度下降（Gradient Descent） 思想，具体步骤如下：

计算梯度：通过反向传播（Backpropagation），计算损失函数对每个模型参数的梯度（导数），梯度方向指示了 “参数变化对损失值的影响方向”（梯度为正，增大参数会使损失增加；梯度为负，增大参数会使损失减少）。
更新参数：根据梯度方向和预设的学习率（Learning Rate，控制参数更新幅度），调整参数。基本公式为： \(\theta_{t+1} = \theta_t - \eta \cdot \nabla L(\theta_t)\) 其中，\(\theta\) 是模型参数，\(\eta\) 是学习率，\(\nabla L(\theta_t)\) 是损失函数在当前参数下的梯度。
迭代优化：重复 “前向传播计算损失→反向传播计算梯度→优化器更新参数” 的过程，直到损失收敛到最小值（或稳定值）。

三、优化器的作用

最小化损失：核心作用是通过调整参数，使损失函数的值尽可能小，从而提升模型预测精度。
加速收敛：基础梯度下降可能收敛缓慢或陷入局部最优，现代优化器（如 Adam）通过引入动量、自适应学习率等机制，显著加快收敛速度。
稳定训练：解决梯度下降中的 “震荡”“梯度消失 / 爆炸” 等问题，确保训练过程稳定（如 RMSprop 通过指数移动平均缓解梯度波动）。
适配场景：不同任务（如小数据集、大规模分布式训练）需要不同优化器，例如 SGD 适合需要精细调优的场景，Adam 适合快速迭代的场景。

四、常用优化器

根据对梯度和学习率的处理方式，常用优化器可分为以下几类：

1. 基础梯度下降类

SGD（Stochastic Gradient Descent，随机梯度下降）
- 原理：每次随机选取一个样本（或小批量样本）计算梯度并更新参数（而非全量数据，降低计算成本）。
- 公式：
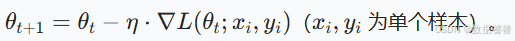
- 优点：计算高效，适合大规模数据。
- 缺点：收敛路径震荡，可能陷入局部最优，学习率需手动调整。

2. 动量优化类（缓解震荡，加速收敛）

SGD + Momentum（动量 SGD）
- 原理：模拟物理中的 “动量” 概念，累加历史梯度的指数移动平均（相当于 “惯性”），减少震荡并加速收敛。
- 公式：
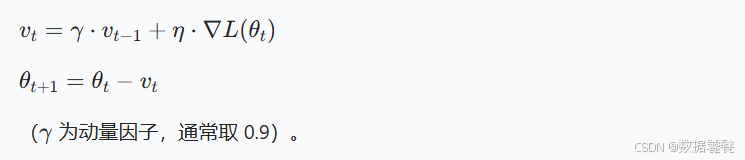
- 优点：比纯 SGD 收敛更快，减少在平缓区域的震荡。

3. 自适应学习率类（自动调整学习率，更智能）

RMSprop（Root Mean Square Propagation）
- 原理：对梯度的平方进行指数移动平均，用其平方根调整学习率（梯度大的参数学习率小，梯度小的参数学习率大），缓解学习率选择难题。
- 公式：
- 为衰减率，通常取 0.9；\(\epsilon\) 为防止除零的小常数）。
- 优点：适合处理非平稳目标（如递归神经网络 RNN）。
Adam（Adaptive Moment Estimation）
- 原理：结合 Momentum（动量）和 RMSprop（自适应学习率）的优点，同时跟踪梯度的一阶矩（均值）和二阶矩（方差），动态调整学习率。
- 公式：
- 优点：收敛快、稳定性好，是目前最常用的优化器之一，适用于大多数场景（图像、文本、推荐等）。

4. 其他优化器

Adagrad：自适应学习率，但学习率随迭代单调递减，可能导致后期收敛停滞。
Adadelta：改进 Adagrad，无需预设学习率，通过历史梯度平方的窗口平均调整更新幅度。
NAdam：结合 Nesterov 动量和 Adam，在某些场景下收敛更稳定。

五、PyTorch 优化器的实现与实例程序

PyTorch 的torch.optim模块内置了所有常用优化器，使用步骤如下：

定义模型（如nn.Linear、nn.Conv2d等）；
初始化优化器，传入模型参数和超参数（如学习率）；
训练循环中：
- 前向传播计算预测值；
- 计算损失（通过损失函数）；
- 调用optimizer.zero_grad()清零梯度（避免累积）；
- 调用loss.backward()反向传播计算梯度；
- 调用optimizer.step()更新参数。

以下是对比不同优化器在回归任务上表现的实例：

PyTorch常用优化器实例

import torch
import torch.nn as nn
import matplotlib.pyplot as plt# ------------------------------
# 1. 准备数据（模拟y=2x+1的回归任务，加入噪声）
# ------------------------------
torch.manual_seed(42)  # 固定随机种子，保证结果可复现
x = torch.linspace(-1, 1, 100).view(-1, 1)  # 输入：100个[-1,1]的点，形状(100,1)
y_true = 2 * x + 1 + 0.2 * torch.randn_like(x)  # 真实值：y=2x+1 + 噪声# ------------------------------
# 2. 定义模型（简单线性模型）
# ------------------------------
class LinearModel(nn.Module):def __init__(self):super().__init__()self.linear = nn.Linear(in_features=1, out_features=1)  # y = wx + bdef forward(self, x):return self.linear(x)# ------------------------------
# 3. 定义训练函数（对比不同优化器）
# ------------------------------
def train(optimizer_name, optimizer, epochs=100):model = LinearModel()  # 每次训练用新模型criterion = nn.MSELoss()  # 损失函数：均方误差losses = []  # 记录每轮损失for epoch in range(epochs):# 前向传播：计算预测值y_pred = model(x)# 计算损失loss = criterion(y_pred, y_true)losses.append(loss.item())# 优化器步骤optimizer.zero_grad()  # 清零梯度loss.backward()        # 反向传播计算梯度optimizer.step()       # 更新参数# 每20轮打印一次损失if (epoch + 1) % 20 == 0:w, b = model.linear.weight.item(), model.linear.bias.item()print(f"{optimizer_name} - Epoch {epoch+1}: 损失={loss.item():.4f}, w={w:.4f}, b={b:.4f}")return losses, model# ------------------------------
# 4. 初始化不同优化器并训练
# ------------------------------
# 模型参数（所有优化器共享同一模型结构的参数引用）
model = LinearModel()
params = model.parameters()# 定义优化器（学习率均设为0.01，公平对比）
optimizers = {"SGD": torch.optim.SGD(params, lr=0.01),"SGD+Momentum": torch.optim.SGD(params, lr=0.01, momentum=0.9),  # 加入动量"Adam": torch.optim.Adam(params, lr=0.01)  # Adam默认参数
}# 训练并记录损失
loss_records = {}
for name, opt in optimizers.items():print(f"\n===== 开始训练 {name} =====")losses, _ = train(name, opt)loss_records[name] = losses# ------------------------------
# 5. 可视化不同优化器的损失下降曲线
# ------------------------------
plt.figure(figsize=(10, 6))
for name, losses in loss_records.items():plt.plot(losses, label=name)
plt.xlabel("Epoch")
plt.ylabel("MSE Loss")
plt.title("不同优化器的损失下降曲线")
plt.legend()
plt.grid(alpha=0.3)
plt.show()

代码说明

任务设计：模拟一个简单的线性回归任务（\(y=2x+1\)），加入噪声增加难度，目标是让模型学习到接近真实值的权重w（接近 2）和偏置b（接近 1）。
优化器对比：
- SGD：损失下降较慢，后期可能震荡；
- SGD+Momentum：借助动量加速收敛，损失下降更快；
- Adam：结合动量和自适应学习率，收敛速度最快，损失最低。
核心步骤：
- optimizer.zero_grad()：必须在反向传播前清零梯度，否则梯度会累积，导致更新错误；
- loss.backward()：计算损失对所有可训练参数的梯度；
- optimizer.step()：根据梯度和优化器规则更新参数。

总结

优化器是模型训练的 “引擎”，通过梯度调整参数以最小化损失；
基础优化器（如 SGD）简单但效率低，现代优化器（如 Adam）通过动量和自适应学习率大幅提升性能；
实际应用中，Adam 通常作为默认选择（收敛快、稳定性好），但在需要精细调优的场景（如深度学习竞赛），SGD+Momentum 可能获得更好的最终性能。

查看全文

http://www.dtcms.com/a/324639.html