机器学习——DBSCAN

一·概念介绍

有监督学习有外部结果y，无监督学习无外部结果y，此为二者核心区别。

概念：
基于密度的带噪声的空间聚类应用算法，它是将簇定义为密度相连的点的最大集合，能够把具有足够高密度的区域划分为簇，并在噪声的空间数据集中发现任意形状的聚类。

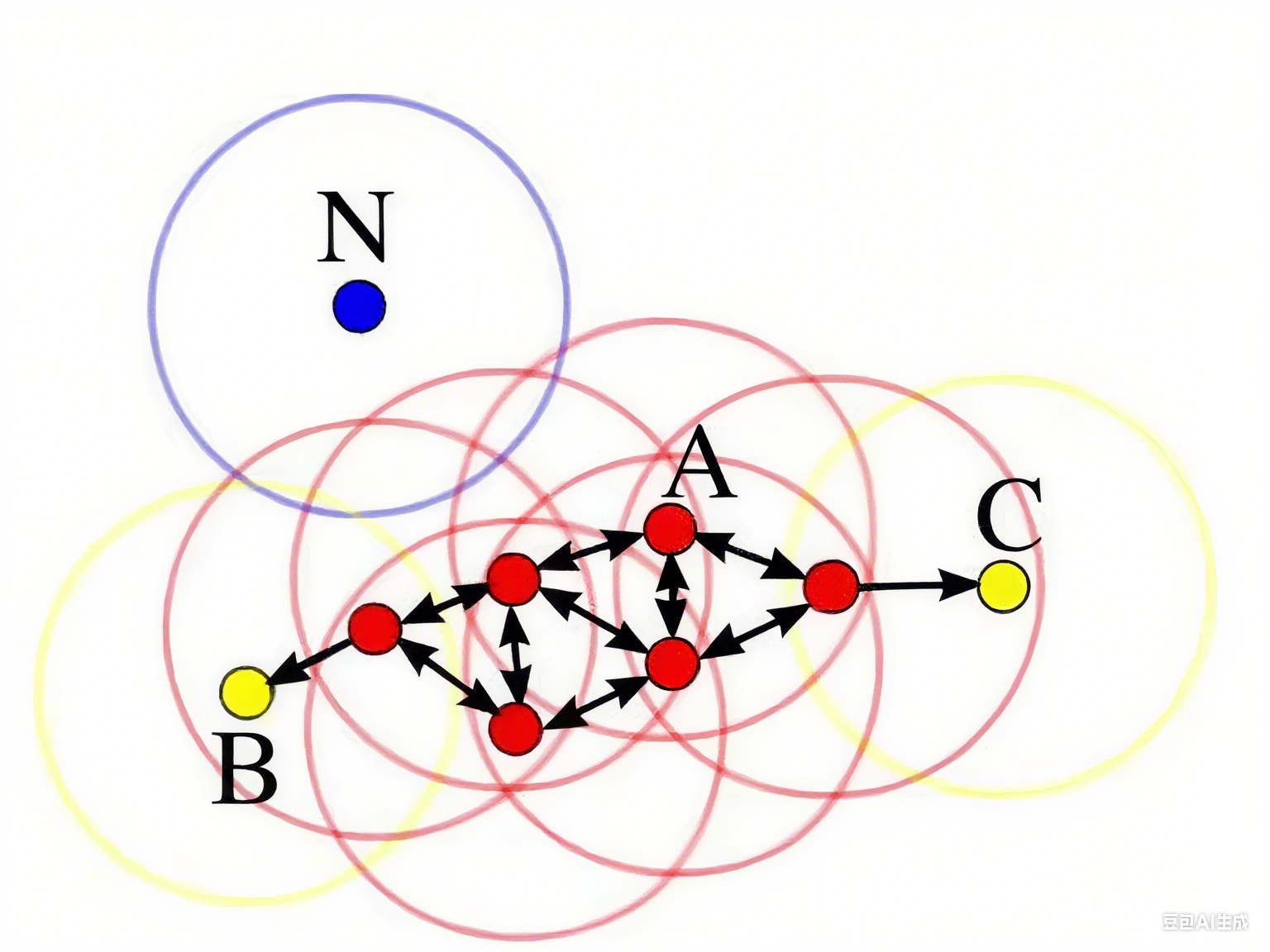
要点：
1. 核心对象：A 点
2.E 邻域：给定对象半径为 E 内的区域
3. 直接密度可达：
4. 密度可达：
5. 边界点：B 点、C 点
6. 离群点：N 点

实现过程

1. 输入数据集
2. 指定半径；
3. 指定密度阈值；

二·参数

1. 初始化参数

python

class sklearn.cluster.DBSCAN(eps=0.5, min_samples=5, metric='euclidean', metric_params=None, algorithm='auto', leaf_size=30, p=None, n_jobs=None
)

2. 各参数详细说明

• eps：DBSCAN 算法中 ε- 邻域的距离阈值。样本距离超过 eps 的样本点不在 ε- 邻域内，默认值 0.5 ，需通过多组值选合适阈值。eps 过大，更多点落入核心对象 ε- 邻域，类别数可能减少；过小则类别数可能增大，原本一类的样本会被分开。
• min_samples：样本点成为核心对象所需的 ε- 邻域样本数阈值，默认值 5 ，常和 eps 一起调参。min_samples 过大，核心对象过少，簇内样本可能被标为噪音点，类别数变多；过小会产生大量核心对象，可能导致类别数过少。
• metric：最近邻距离度量参数，常用默认欧式距离（p=2 的闵可夫斯基距离 ）即可满足需求，可选值还有：
  • 欧式距离 “euclidean”
  • 曼哈顿距离 “manhattan”
  • 切比雪夫距离 “chebyshev”
• metric_params：距离度量的额外参数，一般用默认值 None 即可。
• algorithm：最近邻搜索算法参数，有三种实现方式及四种可选输入：
  • 'brute'：蛮力实现
  • 'kd_tree'：KD 树实现
  • 'ball_tree'：球树实现
  • 'auto'：在上述三种算法中权衡选最优。若输入样本特征稀疏，最终会用 'brute' 。一般默认 'auto' 即可，数据量大 / 特征多且 'auto' 建树慢时，可按需调整。
• leaf_size：构建 KD 树或球树时的叶节点大小，默认值 30 ，会影响树的构建速度和查询效率，一般用默认值。
• p：闵可夫斯基距离中 p 的值，p=1 对应曼哈顿距离，p=2 对应欧式距离，默认 None （此时用默认欧式距离 ）。
• n_jobs：用于并行计算的 CPU 核心数，None 表示用 1 个核心，-1 表示用所有可用核心，可加速最近邻搜索等过程。

3. 属性

• labels_：训练后，存储每个样本点的分类标签，用于标识样本所属的簇（包括噪音点，噪音点标签通常为 -1 ）。

三·代码

import pandas as pd
from sklearn.cluster import DBSCAN
from sklearn import metrics# 读取文件
beer = pd.read_table("data.txt", sep=' ', encoding='utf8', engine='python')
# 传入变量（列名）
X = beer[["calories", "sodium", "alcohol", "cost"]]
# DBSCAN聚类分析
"""
eps:半径
min_samples: 最小密度  【就是圆内最少有几个样本点】
labels: 分类结果  【自动分类，-1为离群点】
"""
db = DBSCAN(eps=20, min_samples=2).fit(X)#归一化，
labels = db.labels_# 添加结果至原数据框
"""
metrics.silhouette_score轮廓评价函数，它是聚类模型优劣的一种评估方式，可用于对聚类结果进行评
X:数据集  scaled_cluster: 聚类结果
score: 非标准化聚类结果的轮廓系数->聚类
"""score = metrics.silhouette_score(X, beer.cluster_db)
print(score)#作业: KNN的寝室。 y 暂时不用y，用kmens或dbscan来训练。 将一部分作为测试集，测试一下效果

1. 导入所需库

首先导入了进行数据分析和聚类所需的库：

• pandas：用于数据读取和处理
• DBSCAN：来自 scikit-learn 的密度聚类算法
• metrics：来自 scikit-learn，用于聚类结果评估

python

运行

import pandas as pd
from sklearn.cluster import DBSCAN
from sklearn import metrics

2. 读取数据文件

使用 pandas 的read_table函数读取数据文件：

• 数据文件名为 "data.txt"
• 使用空格作为分隔符（sep=' '）
• 指定编码为 utf8
• 使用 python 引擎解析文件

python

运行

# 读取文件
beer = pd.read_table("data.txt", sep=' ', encoding='utf8', engine='python')

3. 准备特征数据

从读取的数据中选取需要用于聚类分析的特征列：

• 选取了 "calories"（卡路里）、"sodium"（钠含量）、"alcohol"（酒精含量）和 "cost"（成本）这四个特征
• 这些特征数据将作为 DBSCAN 算法的输入

python

运行

# 传入变量（列名）
X = beer[["calories", "sodium", "alcohol", "cost"]]

4. 执行 DBSCAN 聚类

使用 DBSCAN 算法进行聚类分析：

• eps=20：设置聚类的半径为 20
• min_samples=2：设置每个聚类的最小样本数为 2（即一个聚类至少需要包含 2 个样本）
• fit(X)：对特征数据 X 执行聚类
• labels_：获取聚类结果标签，其中 - 1 表示离群点

python

运行

# DBSCAN聚类分析
"""
eps:半径
min_samples: 最小密度  【就是圆内最少有几个样本点】
labels: 分类结果  【自动分类，-1为离群点】
"""
db = DBSCAN(eps=20, min_samples=2).fit(X)#归一化，
labels = db.labels_

5. 评估聚类结果

使用轮廓系数（silhouette score）评估聚类效果：

• 轮廓系数取值范围为 [-1, 1]
• 接近 1 表示聚类效果好，样本与自身聚类中的样本更相似
• 接近 - 1 表示聚类效果差，样本更应该属于其他聚类

python

运行

# 计算轮廓系数评估聚类结果
"""
metrics.silhouette_score轮廓评价函数，它是聚类模型优劣的一种评估方式，可用于对聚类结果进行评
X:数据集  labels: 聚类结果
score: 聚类结果的轮廓系数
"""
score = metrics.silhouette_score(X, labels)
print(score)

注意事项

原代码中有一处笔误，beer.cluster_db应该改为labels，因为聚类结果存储在labels变量中，而不是beer数据框的cluster_db列中（该列尚未创建）。上面的代码已经修正了这一问题。

如果需要将聚类结果添加到原数据框中，可以添加以下代码：

python

运行

# 添加聚类结果到原数据框
beer['cluster_db'] = labels

上面呢是轮廓系数，下面的是分类指标做的

总代码

import os
import pandas as pdfile_path = "datingTestSet2.txt"
if not os.path.exists(file_path):print(f"Error: File '{file_path}' not found")exit(1)try:data = pd.read_csv(file_path, sep=None, engine='python')
except Exception as e:print(f"File read error: {e}")exit(1)X = data.iloc[:, :-1]
y_true = data.iloc[:, -1].astype(int)import numpy as np
from scipy.optimize import linear_sum_assignmentdef align_labels(true_labels, cluster_labels):unique_true = np.unique(true_labels)unique_cluster = np.unique(cluster_labels)n_true = len(unique_true)n_cluster = len(unique_cluster)# 取较小的类别数作为矩阵维度，避免不匹配n = min(n_true, n_cluster)cost_matrix = np.zeros((n, n))for i in range(n):for j in range(n):cost_matrix[i, j] = -np.sum((true_labels == unique_true[i]) & (cluster_labels == unique_cluster[j]))row_ind, col_ind = linear_sum_assignment(cost_matrix)label_map = {}# 只映射存在的索引，避免越界for i, j in zip(row_ind, col_ind):if j < len(unique_cluster) and i < len(unique_true):label_map[unique_cluster[j]] = unique_true[i]aligned_labels = np.array([label_map.get(c, -1) for c in cluster_labels])return aligned_labelsfrom sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_scorek_values = [2, 3, 4, 5]
metrics_kmeans = {'accuracy': [], 'precision': [], 'recall': [], 'f1': []}for k in k_values:kmeans = KMeans(n_clusters=k, random_state=42).fit(X)aligned_labels = align_labels(y_true, kmeans.labels_)mask = aligned_labels != -1if np.sum(mask) > 0:acc = accuracy_score(y_true[mask], aligned_labels[mask])prec = precision_score(y_true[mask], aligned_labels[mask], average='macro', zero_division=0)rec = recall_score(y_true[mask], aligned_labels[mask], average='macro', zero_division=0)f1 = f1_score(y_true[mask], aligned_labels[mask], average='macro', zero_division=0)metrics_kmeans['accuracy'].append(acc)metrics_kmeans['precision'].append(prec)metrics_kmeans['recall'].append(rec)metrics_kmeans['f1'].append(f1)print(f"KMeans(k={k}) - Acc: {acc:.3f}, Prec: {prec:.3f}, Rec: {rec:.3f}, F1: {f1:.3f}")plt.figure(figsize=(12, 8))
for i, metric in enumerate(metrics_kmeans.keys()):plt.subplot(2, 2, i + 1)plt.plot(k_values, metrics_kmeans[metric], 'o-')plt.xlabel('k')plt.ylabel(metric)plt.title(f'KMeans {metric}')plt.tight_layout()
plt.show()from sklearn.cluster import DBSCANdb = DBSCAN(eps=0.5, min_samples=5).fit(X)
db_labels = db.labels_mask_noise = db_labels != -1
if np.sum(mask_noise) > 0:aligned_db_labels = align_labels(y_true[mask_noise], db_labels[mask_noise])acc_db = accuracy_score(y_true[mask_noise], aligned_db_labels)prec_db = precision_score(y_true[mask_noise], aligned_db_labels, average='macro', zero_division=0)rec_db = recall_score(y_true[mask_noise], aligned_db_labels, average='macro', zero_division=0)f1_db = f1_score(y_true[mask_noise], aligned_db_labels, average='macro', zero_division=0)print(f"\nDBSCAN - Acc: {acc_db:.3f}, Prec: {prec_db:.3f}, Rec: {rec_db:.3f}, F1: {f1_db:.3f}")
else:print("\nDBSCAN: Too many noise points, cannot calculate metrics")data['db_cluster'] = db_labels
print("\nSample results:")
print(data.head(10))

这段代码是上一个聚类分析代码的改进版本，核心区别在于评估指标的变化：上一个代码使用轮廓系数（聚类专用指标，适用于无真实标签的情况），而本代码因为有真实标签（y_true），所以采用了分类任务中常用的评估指标（准确率、精确率、召回率、F1 值）来更直观地衡量聚类效果与真实类别的匹配程度。

1. 导入基础库与文件处理

首先导入基础工具库，检查并读取数据文件：

• os：用于检查文件是否存在
• pandas：用于数据读取和处理

python

运行

import os
import pandas as pdfile_path = "datingTestSet2.txt"
if not os.path.exists(file_path):print(f"Error: File '{file_path}' not found")exit(1)try:data = pd.read_csv(file_path, sep=None, engine='python')  # 自动识别分隔符读取数据
except Exception as e:print(f"File read error: {e}")exit(1)

2. 准备特征数据与真实标签

从读取的数据中拆分出特征和真实标签（用于后续评估聚类效果）：

• X：所有行，除最后一列外的列（特征数据）
• y_true：所有行的最后一列（真实类别标签，转为整数类型）

python

运行

X = data.iloc[:, :-1]  # 特征数据（所有特征列）
y_true = data.iloc[:, -1].astype(int)  # 真实标签（最后一列）

3. 导入标签对齐所需库

聚类算法输出的标签仅代表类别编号（与真实标签的编号可能不一致），需要通过标签对齐将聚类标签映射到真实标签：

• numpy：用于数值计算
• linear_sum_assignment：用于找到最优标签映射关系（匈牙利算法）

python

运行

import numpy as np
from scipy.optimize import linear_sum_assignment

4. 定义标签对齐函数

align_labels函数的作用是将聚类输出的标签（cluster_labels）与真实标签（true_labels）进行映射，解决 “类别编号不匹配” 问题：

• 构建成本矩阵：计算聚类标签与真实标签的匹配程度
• 用匈牙利算法找到最优映射关系
• 将聚类标签转换为与真实标签一致的编号（无法映射的标签记为 - 1）

python

运行

def align_labels(true_labels, cluster_labels):unique_true = np.unique(true_labels)  # 真实标签的唯一值unique_cluster = np.unique(cluster_labels)  # 聚类标签的唯一值n_true = len(unique_true)n_cluster = len(unique_cluster)# 取较小的类别数作为矩阵维度，避免不匹配n = min(n_true, n_cluster)cost_matrix = np.zeros((n, n))# 构建成本矩阵（值越小表示匹配度越高）for i in range(n):for j in range(n):# 计算聚类标签j与真实标签i的重叠数量（取负号转为成本）cost_matrix[i, j] = -np.sum((true_labels == unique_true[i]) & (cluster_labels == unique_cluster[j]))# 用匈牙利算法找到最优映射row_ind, col_ind = linear_sum_assignment(cost_matrix)label_map = {}# 构建映射关系（聚类标签→真实标签）for i, j in zip(row_ind, col_ind):if j < len(unique_cluster) and i < len(unique_true):label_map[unique_cluster[j]] = unique_true[i]# 将聚类标签转换为映射后的真实标签格式aligned_labels = np.array([label_map.get(c, -1) for c in cluster_labels])return aligned_labels

5. 导入 KMeans 聚类与评估库

导入 KMeans 算法、绘图工具和分类评估指标：

• KMeans：聚类算法
• matplotlib.pyplot：用于绘制指标变化图
• 分类评估指标：accuracy_score（准确率）、precision_score（精确率）等

python

运行

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

6. 执行 KMeans 聚类与评估

尝试不同的聚类数（k=2,3,4,5），对每个k进行聚类并评估：

• 聚类后通过align_labels对齐标签
• 过滤无法映射的标签（-1），计算评估指标
• 存储指标结果并打印

python运行

k_values = [2, 3, 4, 5]  # 尝试的聚类数
metrics_kmeans = {'accuracy': [], 'precision': [], 'recall': [], 'f1': []}  # 存储各指标结果for k in k_values:# 训练KMeans模型kmeans = KMeans(n_clusters=k, random_state=42).fit(X)# 对齐聚类标签与真实标签aligned_labels = align_labels(y_true, kmeans.labels_)# 过滤无法映射的标签（仅保留有效标签）mask = aligned_labels != -1if np.sum(mask) > 0:# 计算评估指标acc = accuracy_score(y_true[mask], aligned_labels[mask])prec = precision_score(y_true[mask], aligned_labels[mask], average='macro', zero_division=0)rec = recall_score(y_true[mask], aligned_labels[mask], average='macro', zero_division=0)f1 = f1_score(y_true[mask], aligned_labels[mask], average='macro', zero_division=0)# 存储指标metrics_kmeans['accuracy'].append(acc)metrics_kmeans['precision'].append(prec)metrics_kmeans['recall'].append(rec)metrics_kmeans['f1'].append(f1)# 打印结果print(f"KMeans(k={k}) - Acc: {acc:.3f}, Prec: {prec:.3f}, Rec: {rec:.3f}, F1: {f1:.3f}")

7. 绘制 KMeans 指标变化图

用子图展示不同k值下各评估指标的变化趋势，直观对比聚类效果：

python运行

plt.figure(figsize=(12, 8))
for i, metric in enumerate(metrics_kmeans.keys()):plt.subplot(2, 2, i + 1)  # 2行2列子图plt.plot(k_values, metrics_kmeans[metric], 'o-')  # 绘制折线图plt.xlabel('k')  # x轴：聚类数kplt.ylabel(metric)  # y轴：评估指标plt.title(f'KMeans {metric}')  # 子图标题plt.tight_layout()  # 调整布局
plt.show()  # 显示图像

8. 执行 DBSCAN 聚类与评估

使用 DBSCAN 算法进行聚类，同样通过标签对齐和分类指标评估：

• 先过滤噪声点（DBSCAN 中标签为-1的样本）
• 对有效样本的标签进行对齐，计算评估指标并打印
• python运行

from sklearn.cluster import DBSCAN# 训练DBSCAN模型（eps：半径，min_samples：最小样本数）
db = DBSCAN(eps=0.5, min_samples=5).fit(X)
db_labels = db.labels_  # 获取聚类标签（-1为噪声点）# 过滤噪声点
mask_noise = db_labels != -1
if np.sum(mask_noise) > 0:# 对齐有效样本的标签aligned_db_labels = align_labels(y_true[mask_noise], db_labels[mask_noise])# 计算评估指标acc_db = accuracy_score(y_true[mask_noise], aligned_db_labels)prec_db = precision_score(y_true[mask_noise], aligned_db_labels, average='macro', zero_division=0)rec_db = recall_score(y_true[mask_noise], aligned_db_labels, average='macro', zero_division=0)f1_db = f1_score(y_true[mask_noise], aligned_db_labels, average='macro', zero_division=0)# 打印结果print(f"\nDBSCAN - Acc: {acc_db:.3f}, Prec: {prec_db:.3f}, Rec: {rec_db:.3f}, F1: {f1_db:.3f}")
else:print("\nDBSCAN: Too many noise points, cannot calculate metrics")

9. 展示聚类结果样本

将 DBSCAN 的聚类结果添加到原始数据中，打印前 10 行样本，直观查看聚类标签：python

运行

data['db_cluster'] = db_labels  # 添加DBSCAN聚类结果到数据框
print("\nSample results:")
print(data.head(10))  # 显示前10行数据及聚类标签