机器学习 DBScan

目录

深入浅出 DBSCAN：从原理到实战的密度聚类算法详解

K-Means 局限性及 DBSCAN 算法

一、DBSCAN 核心思想：用密度定义 “簇” 的边界

二、DBSCAN 的关键概念：3 个核心定义

1. ε（Epsilon，邻域半径）

2. MinPts（最小样本数）

3. 三种样本类型

三、DBSCAN 工作流程：从样本到簇的形成

关键逻辑：密度可达与密度相连

四、DBSCAN 的优缺点：适用场景与局限性

优点：超越传统聚类的灵活特性

缺点：参数敏感与场景限制

五、DBSCAN 实战：用 Python 实现聚类分析

步骤 1：准备数据与环境

步骤 2：训练 DBSCAN 模型

步骤 3：对比 k-means 结果

步骤 4：可视化聚类结果

结果分析

参数调优技巧

六、DBSCAN 的适用场景与扩展

典型应用场景

扩展算法：HDBSCAN

七、总结：何时选择 DBSCAN？

---

深入浅出 DBSCAN：从原理到实战的密度聚类算法详解

在机器学习的聚类算法家族中，DBSCAN（Density-Based Spatial Clustering of Applications with Noise）以其独特的 “密度视角” 占据着重要地位。与 k-means 等需要预先指定簇数的算法不同，DBSCAN 能自动发现任意形状的簇并识别噪声，这让它在实际场景中备受青睐。本文将带你全面剖析 DBSCAN 的原理、优缺点、适用场景及实战技巧，帮你真正掌握这一强大的聚类工具。

K-Means 局限性及 DBSCAN 算法

• K-Means 缺点：无法处理非球形簇或嵌套簇（如环形分布数据）。
• DBSCAN 原理：
  • 基于密度聚类，通过“感染”机制扩展簇：
    • 核心点：在半径 eps 内至少有 min_samples 个邻居的点。
    • 密度可达：通过核心点传播的连续路径连接的样本。
    • 离群点：未被任何核心点覆盖的样本。
  • 关键参数：
    • eps：邻域半径（默认0.5，需根据数据调整）。
    • min_samples：核心点邻域内最少样本数（默认5）。

一、DBSCAN 核心思想：用密度定义 “簇” 的边界

传统聚类算法（如 k-means）往往假设簇是 “凸形” 或 “球形” 的密集区域，但现实世界的数据分布往往复杂多样 —— 可能是环形、条形甚至不规则形状。DBSCAN 的创新之处在于：它用 “密度” 来定义簇，认为 “簇是由足够密集的样本组成的区域，且该区域与其他密集区域被低密度区域分隔开”。

简单来说，DBSCAN 的核心逻辑可以类比为 “社交圈识别”：在人群中，彼此距离近的人形成小圈子（密集区域），圈子里的人通过朋友互相连接；而离所有圈子都很远的人，就是孤立的 “噪声”。

二、DBSCAN 的关键概念：3 个核心定义

要理解 DBSCAN 的工作原理，需先掌握三个核心概念，它们是算法运行的基础：

1. ε（Epsilon，邻域半径）

ε 是人为设定的距离阈值，表示 “以某个样本为中心，半径为 ε 的圆形区域”，称为该样本的 “ε- 邻域”。例如，若 ε=5，那么距离样本 A 小于等于 5 的所有样本都属于 A 的 ε- 邻域。这个参数决定了 “多近才算近”，直接影响聚类结果的粒度。

2. MinPts（最小样本数）

MinPts 是另一个关键参数，指 “一个样本的 ε- 邻域内至少包含的样本数量（包括该样本自身）”。它定义了 “多密集才算密集”：若某个样本的 ε- 邻域内样本数≥MinPts，则该样本被认为是 “核心样本”，否则为 “非核心样本”。

3. 三种样本类型

基于 ε 和 MinPts，DBSCAN 将样本分为三类：

• 核心点：ε- 邻域内样本数≥MinPts 的样本。核心点是形成簇的 “骨架”，能 “支撑” 起一个密集区域。

• 边界点：ε- 邻域内样本数 < MinPts，但落在某个核心点的 ε- 邻域内的样本。边界点属于其所在核心点的簇，但自身无法成为核心点。

• 噪声点：既不是核心点，也不是任何核心点的 ε- 邻域内的样本。噪声点不被归入任何簇，通常被视为异常值。

三、DBSCAN 工作流程：从样本到簇的形成

DBSCAN 的聚类过程可以概括为 “遍历样本→扩展簇→标记噪声”，具体步骤如下：

1. 初始化：将所有样本标记为 “未访问”。

1. 遍历未访问样本：随机选择一个未访问样本\( p \)，标记为 “已访问”。

1. 判断是否为核心点：计算\( p \)的 ε- 邻域内的样本数。若数量≥MinPts，则\( p \)是核心点，开始构建簇；若不满足，则标记\( p \)为 “噪声点”，继续遍历下一个未访问样本。

1. 扩展簇：以核心点\( p \)为起点，将其 ε- 邻域内的所有样本纳入临时簇。然后对临时簇中所有未访问的样本重复以下操作：

• • 标记样本为 “已访问”；

• • 若该样本是核心点，将其 ε- 邻域内的所有样本加入临时簇（即使这些样本之前未被访问）；

• • 重复扩展，直到没有新样本能加入临时簇，此时临时簇成为一个完整的簇。

1. 重复迭代：回到步骤 2，继续遍历剩余的未访问样本，直到所有样本都被访问。最终形成的所有簇和噪声点共同构成聚类结果。

关键逻辑：密度可达与密度相连

在扩展簇的过程中，DBSCAN 通过 “密度可达” 和 “密度相连” 来定义簇的范围：

• 密度可达：若存在样本链\( p_1, p_2, ..., p_n \)，其中\( p_1 = p \)，\( p_n = q \)，且每个\( p_i \)都是核心点，且\( p_{i+1} \)在\( p_i \)的 ε- 邻域内，则称\( q \)从\( p \)密度可达。

• 密度相连：若存在样本\( o \)，使得\( p \)和\( q \)都从\( o \)密度可达，则称\( p \)和\( q \)密度相连。一个簇就是由所有相互密度相连的样本组成的集合。

四、DBSCAN 的优缺点：适用场景与局限性

优点：超越传统聚类的灵活特性

• 无需预先指定簇数：与 k-means 不同，DBSCAN 不需要人工设定簇的数量，算法会根据数据密度自动划分簇，这在未知数据分布时非常实用。

• 能发现任意形状的簇：无论是环形、条形还是不规则形状的簇，只要密度足够，DBSCAN 都能准确识别，而 k-means 等算法仅适用于凸形簇。

• 自带噪声识别功能：算法天然能区分噪声点，无需额外的异常检测步骤，这在欺诈检测、故障识别等场景中很有价值。

• 对异常值不敏感：噪声点被单独标记，不会像 k-means 那样因离群点导致簇中心偏移。

缺点：参数敏感与场景限制

• 对参数 ε 和 MinPts 高度敏感：这两个参数的微小变化可能导致聚类结果大幅不同，且没有通用的最优值，需要结合领域知识或通过数据探索确定。

• 不擅长处理密度不均匀的数据：若数据中不同簇的密度差异较大（如一个簇密集、一个簇稀疏），同一组 ε 和 MinPts 难以兼顾所有簇。

• 高维数据效果下降：在高维空间中，“距离” 的定义变得模糊（维度灾难），ε- 邻域的意义被削弱，需先通过 PCA 等方法降维。

• 计算复杂度较高：在未优化的情况下，时间复杂度为\( O(n^2) \)（\( n \)为样本数），样本量过大时效率较低（可通过空间索引如 KD 树优化至\( O(n\log n) \)）。

五、DBSCAN 实战：用 Python 实现聚类分析

下面以 scikit-learn 库为例，展示 DBSCAN 的实战流程。我们将使用经典的 “月牙形数据”（非凸分布），对比 DBSCAN 与 k-means 的效果差异。

步骤 1：准备数据与环境

import numpy as npimport matplotlib.pyplot as pltfrom sklearn.datasets import make_moonsfrom sklearn.cluster import DBSCAN, KMeansfrom sklearn.preprocessing import StandardScaler# 生成月牙形数据（含噪声）X, y_true = make_moons(n_samples=300, noise=0.05, random_state=42)# 数据标准化（距离类算法的必要步骤）X = StandardScaler().fit_transform(X)

步骤 2：训练 DBSCAN 模型

# 设定参数：ε=0.3，MinPts=5（可根据数据调整）dbscan = DBSCAN(eps=0.3, min_samples=5)y_dbscan = dbscan.fit_predict(X)

步骤 3：对比 k-means 结果

# k-means（需指定簇数k=2）kmeans = KMeans(n_clusters=2, random_state=42)y_kmeans = kmeans.fit_predict(X)

步骤 4：可视化聚类结果

plt.figure(figsize=(12, 5))# DBSCAN结果plt.subplot(121)plt.scatter(X[:, 0], X[:, 1], c=y_dbscan, cmap='viridis', s=50)plt.title('DBSCAN Clustering Result')plt.xlabel('Feature 1')plt.ylabel('Feature 2')# k-means结果plt.subplot(122)plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, cmap='viridis', s=50)plt.title('k-means Clustering Result')plt.xlabel('Feature 1')plt.ylabel('Feature 2')plt.tight_layout()plt.show()

结果分析

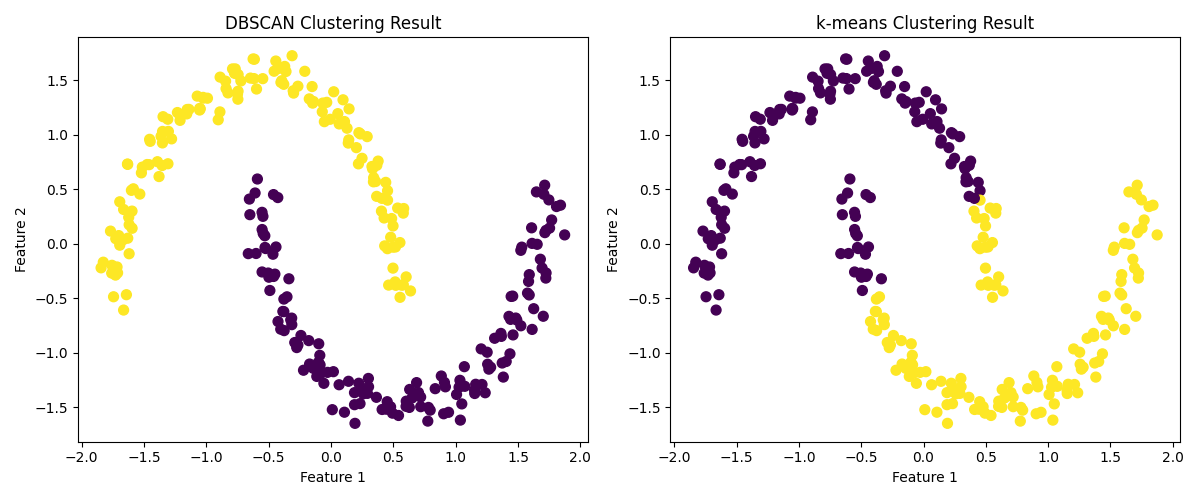
可视化结果会清晰显示：DBSCAN 准确识别了两个月牙形的簇，且未将噪声点归入任何簇；而 k-means 则将月牙形数据强行分割为两个凸形簇，无法捕捉真实的数据分布。这直观体现了 DBSCAN 处理非凸簇的优势。

参数调优技巧

• ε 的选择：可通过 “k - 距离图” 确定：计算每个样本到其第 k 个最近邻的距离，排序后绘制折线图，找到 “拐点” 对应的距离作为 ε（拐点处距离突然增大，代表密集区域的边界）。

• MinPts 的选择：通常设为 “维度 + 1”（如二维数据设为 3），或根据领域知识调整（样本越密集，MinPts 可越大）。

六、DBSCAN 的适用场景与扩展

典型应用场景

• 空间数据聚类：如地理位置聚类（识别城市中的商圈、居民区）、地图 POI（兴趣点）分组。

• 异常检测：在信用卡欺诈检测、设备故障诊断中，噪声点往往对应异常行为。

• 图像分割：对图像像素按密度聚类，分割出目标区域与背景。

• 文本聚类：将主题相似的文档聚为一类（需先通过 TF-IDF 等方法将文本转为向量）。

扩展算法：HDBSCAN

为解决 DBSCAN 对密度不均匀数据的局限性，研究者提出了 HDBSCAN（Hierarchical DBSCAN）。它通过构建 “密度层次树”，自动适配不同密度的簇，无需手动调整 ε，且对噪声更稳健，是 DBSCAN 的强力升级版本。

七、总结：何时选择 DBSCAN？

DBSCAN 是一款 “以密度为核心” 的聚类算法，当你面临以下场景时，它可能是更好的选择：

• 数据分布是非凸形或不规则形状；

• 不知道数据中簇的具体数量；

• 需要同时进行聚类和异常检测；

• 数据中噪声比例不高，且主要簇的密度相对均匀。

但需注意：DBSCAN 对参数敏感，实际使用中需结合数据探索和领域知识仔细调优；高维数据或超大样本量场景下，建议先降维或考虑优化后的实现版本（如 HDBSCAN）。

掌握 DBSCAN 的原理与技巧，能让你在复杂数据聚类任务中更游刃有余。希望本文能帮助你打开密度聚类的大门，在实际问题中灵活运用这一强大工具！