当前位置：首页 > news >正文

【CF】Day124——杂题 (鸽巢原理 | 构造 | 贪心 + 模拟)

news 2025/8/11 6:30:50

B. Coloring

题目：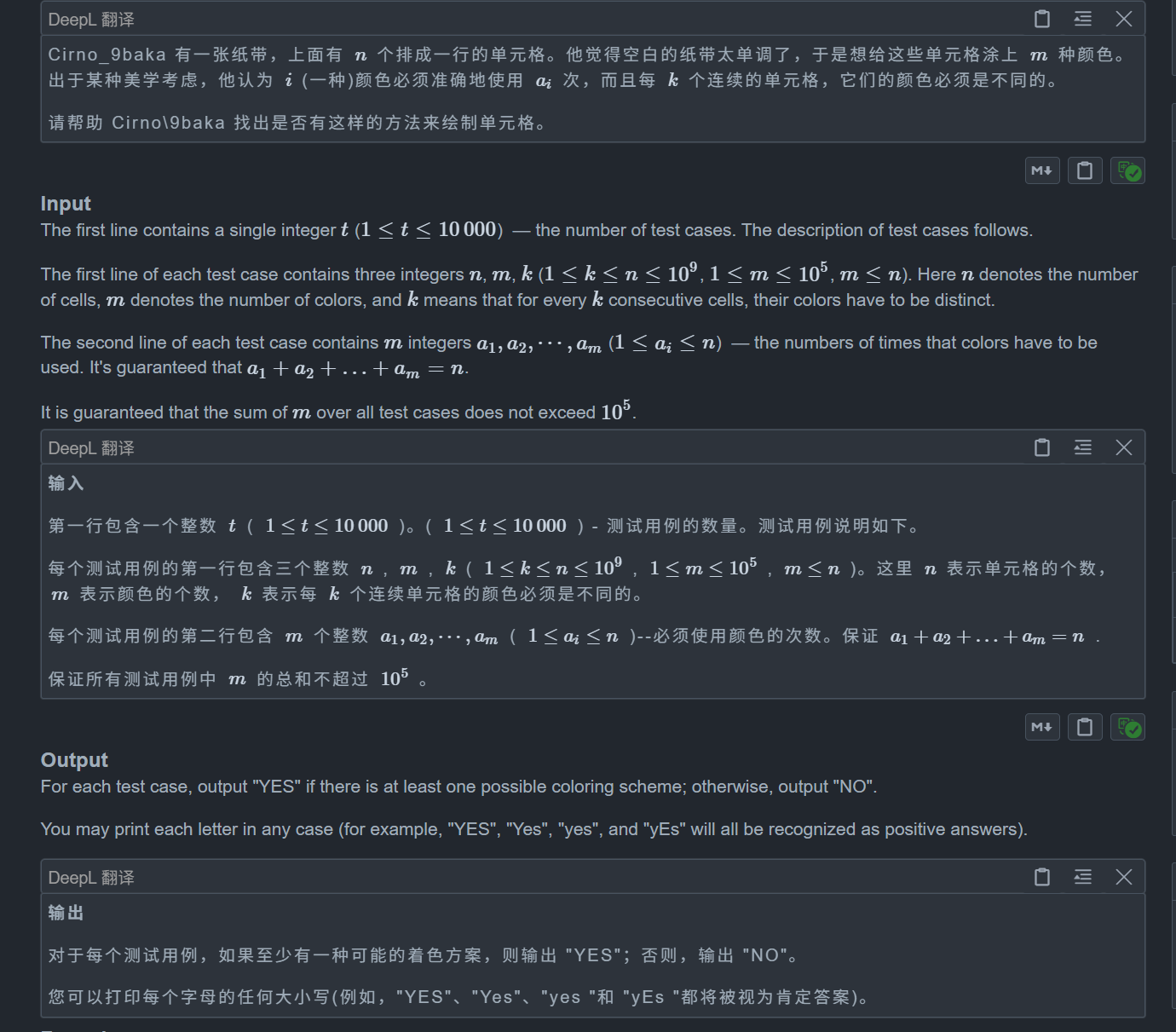

思路：

鸽巢原理

鸽巢原理理解简单，但是实际运用并不简单

这一题我们可以这样思考，把 n 分成 c 个抽屉，其中 c = n / k 向上取整，那么对于前 c - 1 个抽屉其大小均为 k，而最后一个抽屉大小小于等于 k

现在我们考虑放球

如果某个颜色的球大于 c，那么说明必定有一个抽屉会放两个及以上的球，那么此时就是无解的

如果某个颜色的球恰好等于 c，那么我们考虑其能不能放到最后的抽屉，用一个变量 f1 来储存恰好数量为 c 的颜色球数

如果某个颜色小于 c，那么肯定可以放，这是毋庸置疑的

现在考虑等于的情况，我们计算出最后的抽屉大小为 sz，如果有 f1 > sz，那么肯定不行的，否则一定可以

因此按照上面的情况模拟即可

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"void solve()
{int n,m,k;cin >> n >> m >> k;int f1 = 0;int len = (n + k - 1) / k;int flag = 0;for (int i = 0; i < m; i++){int a;cin >> a;if(a == len) f1++;if(a > len) flag = 1;}if(flag){no;return;}if(f1 <= (n - 1) % k + 1) yes;else no;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

C. Ice and Fire

题目：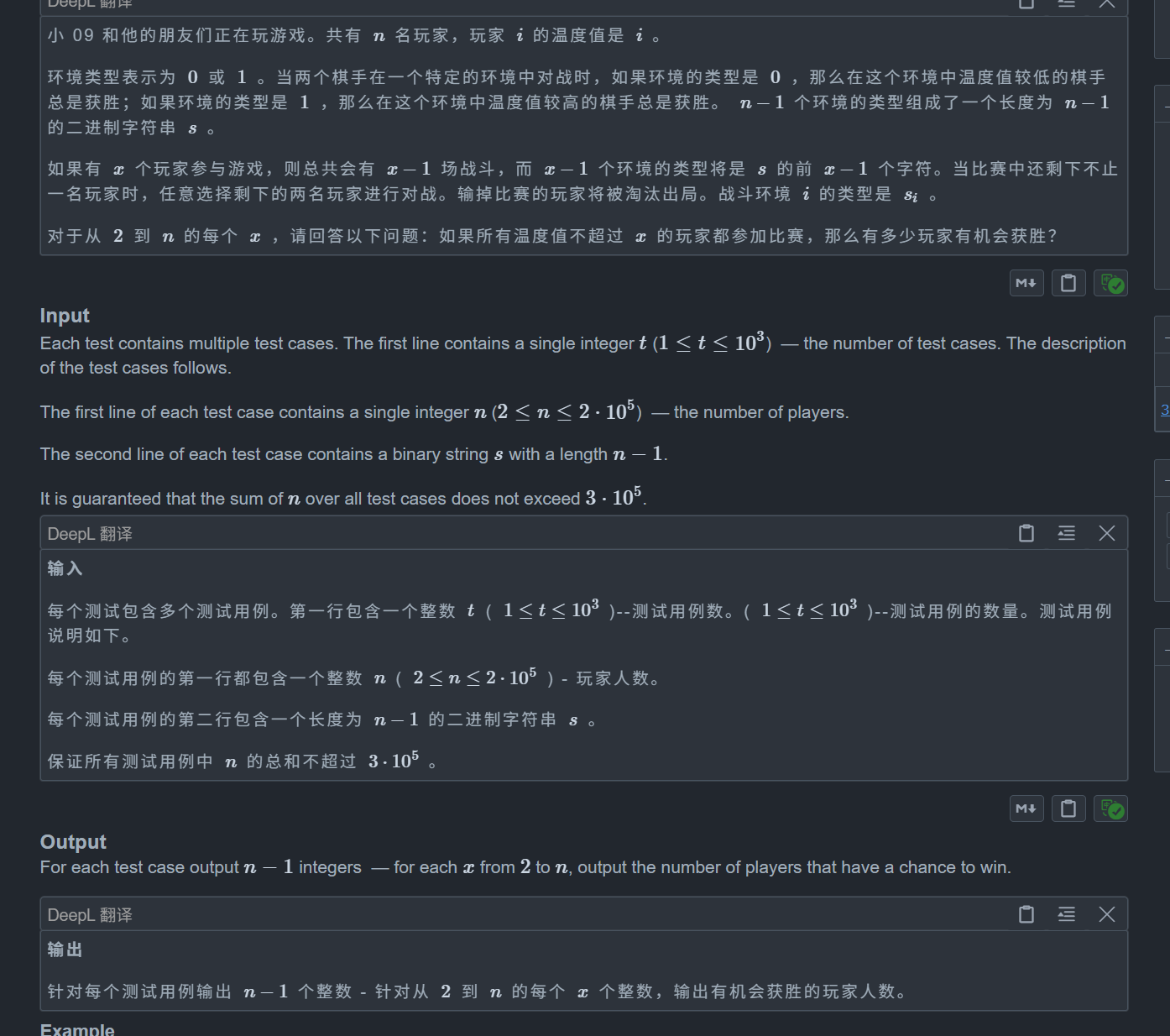

思路：

构造

本题其实是个结论题，我们来考虑观察一下，下面以 1 举例

对于一个字符串，我们令其最后的一段连续 1 字符串长度为 k，那么结论有：

所有 1 ~ k 的人都不可能胜利，所有 k + 1 ~ n 的人都可能胜利

我们来证明一下

对于前半段，如果存在某个 1 ~ k 的人活到了最后一段，那么这个人就要接受 k 次对局，但是 k 次对局要 k + 1 个人，所以即使 1 ~ k 的人全都活下来也会多一个大于 k 的人，最后的胜者一定是大于 k 的人活下来了，因此 1 ~ k 的人不可能胜利

对于后半段，我们假设一个 x 活到了最后 k 轮中（n >= x > k），那么对于前面的所有回合有两种情况，第一种就是全为 0，此时我们只需要不选 x 进行操作即可，同时还能消除所有的比 x 大的数，参考前半段证明；如果既有 0 又有 1 其实也是一样的，我们可以利用最大的数消除比 x 大的数，其作用和 0 类似，最终一定能形成 x 最大的局面，因此 x 一定能获胜

对于连续 0 段其实也是一样的证明

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"void solve()
{int n;cin >> n;string s;cin >> s;int cnt0 = 0,cnt1 = 0;for (int i = 0; i < n-1; i++){if(s[i] == '0') cnt0++,cnt1 = 0;else cnt1++,cnt0 = 0;cout << i + 2 - max(cnt0,cnt1) << " ";}cout << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

D. Same Count One

题目：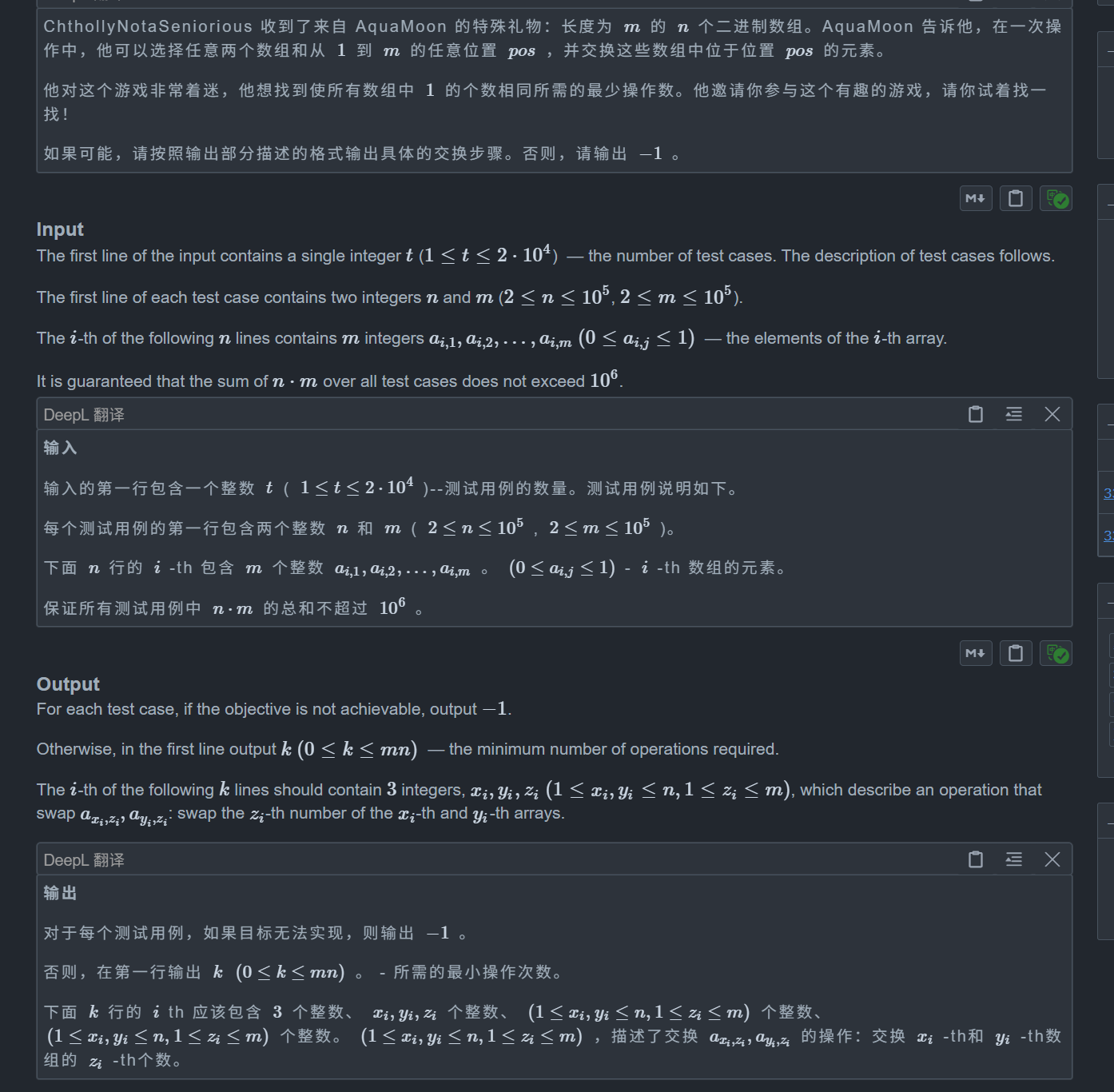

思路：

贪心 + 模拟

首先判断无解，如果所有 1 的数量 sum 不能被 n 整除，及不能平均分给每一行，那么一定无解，否则一定有解，因为 1 是可以行间任意交换的

然后直接模拟即可，我们枚举每一列，考虑判断每一行当前的 1 的数量是不是等于平均值，如果小的话那么就需要，如果大了那么就给出，这样贪心的策略必能保证最小操作

代码也很简单，一道大模拟

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"void solve()
{int n,m;cin >> n >> m;vector<vector<int>> a(n,vector<int>(m,0));vector<int> sum(n,0);int tot = 0;for (int i = 0; i < n; i++){for (int j = 0; j < m; j++){cin >> a[i][j];sum[i] += a[i][j];}tot += sum[i];}if(tot % n){cout << "-1\n";return;}tot /= n;vector<tuple<int,int,int>> ans;vector<int> give,need;//枚举列for (int i = 0; i < m; i++){//枚举行for (int j = 0; j < n; j++){if(sum[j] > tot && a[j][i]) give.push_back(j);if(sum[j] < tot && !a[j][i]) need.push_back(j);}for (int j = 0; j < min(give.size(),need.size()); j++){sum[give[j]]--;sum[need[j]]++;ans.emplace_back(need[j],give[j],i);}give.clear();need.clear();}cout << ans.size() << endl;for(auto & [i,j,k] : ans){cout << i+1 << " " << j+1 << " " << k+1 << endl;}
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}

查看全文

http://www.dtcms.com/a/324167.html