数据结构：树

树与二叉树知识总结

一、树（一对多结构）

（一）树的定义

树是由 ( n(n\geq0) ) 个结点构成的有限集合 。当 ( n = 0 ) 时，称为空树 ；当 ( n>0 ) 时，满足以下条件：

• 有且仅有一个特定的根结点。
• 当 ( n>1 ) 时，其余结点可划分为 ( m(m\geq0) ) 个互不相交的有限集合 ( T_1, T_2, \cdots, T_m )，每个集合本身又是一棵树，称为根的子树。

（二）树的基本概念

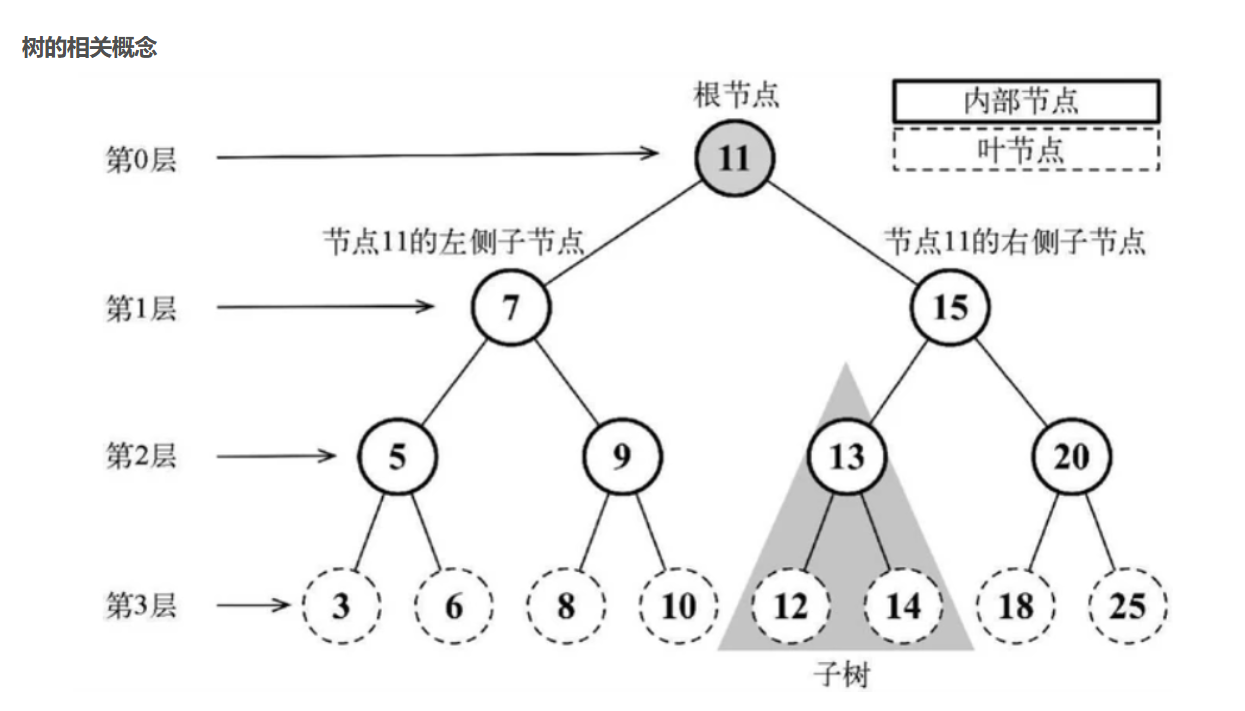
• 结点的度：结点拥有子树的个数。度为 ( 0 ) 的结点是叶结点（叶子结点 ），度不为 ( 0 ) 的结点是分支结点（非叶结点 ）。
• 叶结点：度为0的结点称为叶子结点或终端结点；
• 树的度：树中所有结点的度的最大值。
• 树的深度（高度）：根为第一层，最底层叶子所在层为最后一层，总层数就是树的深度 。
• 树的存储：有顺序结构（按一定规则存储，利于按左小右大等逻辑查找 ）和链式结构（通过指针关联结点 ）两种方式 。

二、二叉树（binary tree ，双分支结构 ）

（一）二叉树特点

• 每个结点最多有两棵子树（左子树、右子树 ）。
• 左子树和右子树是有顺序的，次序不能颠倒 。
• 若结点只有一棵子树，也要区分是左子树还是右子树 。

（二）特殊二叉树

• 左 / 右斜树：只有左子树或者只有右子树的二叉树，形态类似一条斜线 。
• 满二叉树：所有分支结点都有左、右子树，且所有叶子都在同一层。结点数达到理论最大值，深度为 ( k ) 时，结点总数是 ( 2^k - 1 ) 。
• 完全二叉树：结点数小于满二叉树，但结点编号与满二叉树（同深度 ）的结点编号一一对应，叶子集中在底层和次底层，且最后一层叶子靠左分布 。

（三）二叉树性质

1. 第 ( i ) 层（( i\geq1 ) ）最多有 ( 2^{i - 1} ) 个结点 。比如第 2 层，最多 ( 2^{2 - 1}=2 ) 个结点 。
2. 深度为 ( k ) 的二叉树，最多有 ( 2^k - 1 ) 个结点（满二叉树情况 ）。像深度为 3 的满二叉树，结点数是 ( 2^3 - 1 = 7 ) 个 。
3. 对任意二叉树，叶子结点数 ( n_0 ) 与度为 2 的结点数 ( n_2 ) 满足 ( n_0 = n_2 + 1 ) 。可通过结点总数（( n = n_0 + n_1 + n_2 ) ，( n_1 ) 是度为 1 的结点数 ）和边数（( n - 1 = n_1 + 2n_2 ) ，因为根结点没有父边 ）推导得出 。
4. 有 ( n ) 个结点的完全二叉树，深度为 ( \lfloor\log_2 n\rfloor + 1 )（( \lfloor\ \rfloor ) 表示向下取整 ）。例如 ( n = 7 ) ，( \log_2 7\approx2.81 ) ，向下取整加 1 得深度 3 ，符合满二叉树（完全二叉树特殊情况 ）实际 。

三、二叉树遍历（核心是按规则访问每个结点，常用于数据查找、结构分析 ）

遍历就是按一定顺序“走遍”树中所有结点，且每个结点仅访问一次 。主要有以下 4 种方式，以下结合示例树（根结点为 ① ，左子树 ② 带结点 ④ 、⑤ ，右子树 ③ 带结点 ⑥ ，④ 还有子结点 ⑦ ，⑤ 还有子结点 ⑧ ）说明：

（一）层序遍历

• 规则：从上到下、从左到右逐层访问结点 。
• 示例执行：先访问第 1 层根结点 ① ，再第 2 层 ② 、③ ，接着第 3 层 ④ 、⑤ 、⑥ ，最后第 4 层 ⑦ 、⑧ ，顺序为 ①→②→③→④→⑤→⑥→⑦→⑧ 。

（二）前序遍历（根 - 左 - 右 ）

• 规则：先访问根结点，再递归遍历左子树，最后递归遍历右子树 。
• 示例执行：先访问根 ① ；然后遍历 ① 的左子树，左子树的根是 ② ，接着遍历 ② 的左子树（根 ④ ），再遍历 ④ 的左子树（根 ⑦ ，无后续子树返回 ），回到 ④ 遍历右子树（无 ），回到 ② 遍历右子树（根 ⑤ ），遍历 ⑤ 的左子树（根 ⑧ ，无后续 ），回到 ⑤ 遍历右子树（无 ），左子树遍历完；最后遍历 ① 的右子树（根 ③ ），遍历 ③ 的左子树（根 ⑥ ，无后续 ），遍历 ③ 的右子树（无 ）。整体顺序：①→②→④→⑦→⑤→⑧→③→⑥ 。

（三）中序遍历（左 - 根 - 右 ）

• 规则：先递归遍历左子树，访问根结点，再递归遍历右子树 。
• 示例执行：从根 ① 开始，先遍历左子树 ② ，遍历 ② 的左子树 ④ ，遍历 ④ 的左子树 ⑦（无左子树 ），访问 ⑦ （叶子 ），回到 ④ 访问根 ④ ，遍历 ④ 的右子树（无 ），回到 ② 访问根 ② ，遍历 ② 的右子树 ⑤ ，遍历 ⑤ 的左子树 ⑧（无左子树 ），访问 ⑧ ，回到 ⑤ 访问根 ⑤ ，遍历 ⑤ 的右子树（无 ），左子树遍历完；访问根 ① ；遍历右子树 ③ ，遍历 ③ 的左子树 ⑥（无左子树 ），访问 ⑥ ，遍历 ③ 的右子树（无 ），访问根 ③ 。顺序为 ⑦→④→②→⑧→⑤→①→⑥→③ 。

（四）后序遍历（左 - 右 - 根 ）

• 规则：先递归遍历左子树，再递归遍历右子树，最后访问根结点 。
• 示例执行：从根 ① 出发，遍历左子树 ② ，遍历 ② 的左子树 ④ ，遍历 ④ 的左子树 ⑦（无左右子树 ），访问 ⑦ ，遍历 ④ 的右子树（无 ），回到 ④ 访问根 ④ ？不，后序要左右都走完才访问根，所以遍历 ② 的右子树 ⑤ ，遍历 ⑤ 的左子树 ⑧（无左右 ），访问 ⑧ ，遍历 ⑤ 的右子树（无 ），访问根 ⑤ ，回到 ② 访问根 ② ；遍历右子树 ③ ，遍历 ③ 的左子树 ⑥（无左右 ），访问 ⑥ ，遍历 ③ 的右子树（无 ），访问根 ③ ；最后访问根 ① 。顺序为 ⑦→⑧→⑤→④→②→⑥→③→① 。

关于前中后三序遍历的练习：

代码；

树的构造：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef char DATATYPE;
typedef struct BiTNode /* 结点结构 */
{DATATYPE data;                   /* 结点数据 */struct BiTNode *lchild, *rchild; /* 左右孩子指针 */
} BiTNode;
//使用前序（根左右）规则，将空位用#补全，从而表示空，设计字符序列。
char data[] = "Abd#g###ce#h##fi###";
int ind = 0;
void CreateTree(BiTNode **root)
{char c = data[ind++];if ('#' == c){*root=NULL;return;}else{*root = malloc(sizeof(BiTNode));if(*root==NULL){printf("malloc error");return ;}(*root)->data = c;CreateTree(&(*root)->lchild);CreateTree(&(*root)->rchild);}return;
}

前序遍历：根左右

//根左右
void PreOrderTraverse(BiTNode *root)
{if (NULL == root){return;}else{printf("%c", root->data);PreOrderTraverse(root->lchild);PreOrderTraverse(root->rchild);}return;
}

中序遍历：左根右

// 左根右
void InOrderTraverse(BiTNode *root)
{if(NULL==root){return ;}else{InOrderTraverse(root->lchild);printf("%c",root->data);InOrderTraverse(root->rchild);}return;
}

后序遍历：左右根

//左右根
void PostOrderTraverse(BiTNode *root)
{if(NULL==root){return;}else{PostOrderTraverse(root->lchild);PostOrderTraverse(root->rchild);printf("%c",root->data);}return ;
}

层序遍历

#include <stdio.h>
#include <stdlib.h>// 树节点结构定义
struct TreeNode {int data;struct TreeNode *left;struct TreeNode *right;
};// 队列结构定义
struct Queue {struct TreeNode **data;int front;int rear;int capacity;
};// 创建树节点
struct TreeNode* createNode(int data) {struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));node->data = data;node->left = NULL;node->right = NULL;return node;
}// 创建队列
struct Queue* createQueue(int capacity) {struct Queue* queue = (struct Queue*)malloc(sizeof(struct Queue));queue->data = (struct TreeNode**)malloc(sizeof(struct TreeNode*) * capacity);queue->front = queue->rear = -1;queue->capacity = capacity;return queue;
}// 检查队列是否为空
int isEmpty(struct Queue* queue) {return queue->front == -1;
}// 入队操作
void enqueue(struct Queue* queue, struct TreeNode* node) {if (queue->rear == queue->capacity - 1) {printf("队列已满\n");return;}if (isEmpty(queue)) {queue->front = 0;}queue->rear++;queue->data[queue->rear] = node;
}// 出队操作
struct TreeNode* dequeue(struct Queue* queue) {if (isEmpty(queue)) {return NULL;}struct TreeNode* node = queue->data[queue->front];if (queue->front == queue->rear) {queue->front = queue->rear = -1;} else {queue->front++;}return node;
}// 层次遍历函数
void levelOrderTraversal(struct TreeNode* root) {if (root == NULL) {return;}// 创建一个足够大的队列struct Queue* queue = createQueue(100);enqueue(queue, root);printf("层次遍历结果: ");while (!isEmpty(queue)) {struct TreeNode* current = dequeue(queue);printf("%d ", current->data);// 将左子节点入队if (current->left != NULL) {enqueue(queue, current->left);}// 将右子节点入队if (current->right != NULL) {enqueue(queue, current->right);}}printf("\n");// 释放队列内存free(queue->data);free(queue);
}// 释放树的内存
void freeTree(struct TreeNode* root) {if (root == NULL) return;freeTree(root->left);freeTree(root->right);free(root);
}int main() {// 创建一个测试树/*1/   \2     3/ \   / \4   5 6   7*/struct TreeNode* root = createNode(1);root->left = createNode(2);root->right = createNode(3);root->left->left = createNode(4);root->left->right = createNode(5);root->right->left = createNode(6);root->right->right = createNode(7);// 执行层次遍历levelOrderTraversal(root);// 释放树内存freeTree(root);return 0;
}