当前位置：首页 > news >正文

基于遗传优化的稀疏线阵最优排布算法matlab仿真

news 2025/8/10 7:44:58

1.程序功能描述

2.测试软件版本以及运行结果展示

3.部分程序

4.算法理论概述

5.参考文献

6.完整程序

1.程序功能描述

稀疏线阵的核心挑战是在给定阵元数量的情况下，通过调整阵元位置，使天线阵列的波束方向图满足预设性能指标（如副瓣电平等）。遗传算法（Genetic Algorithm, GA）通过模拟自然选择、交叉、变异等生物进化过程，在解空间中高效搜索最优阵元排布方案。

2.测试软件版本以及运行结果展示

MATLAB2022A/MATLAB2024B版本运行

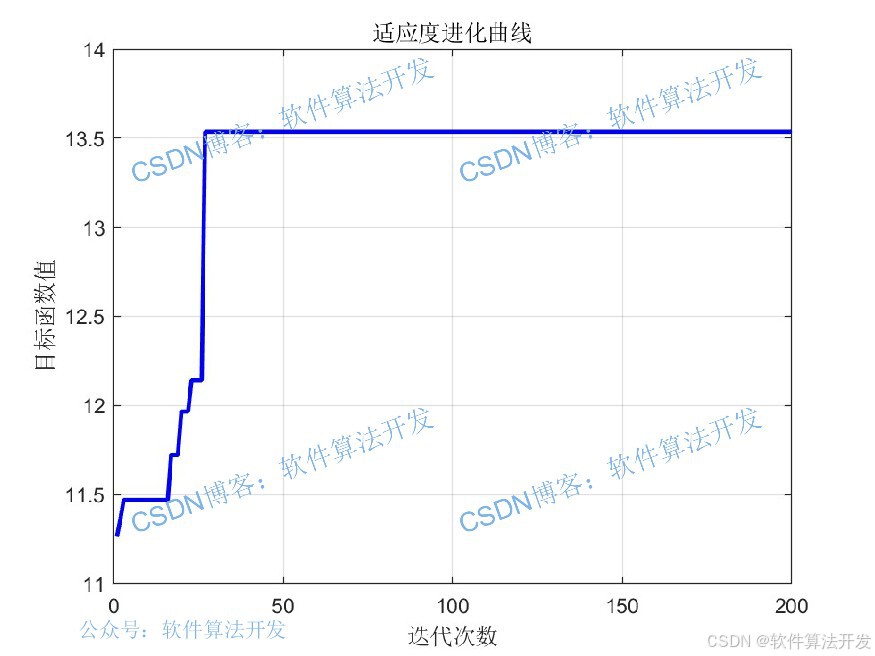
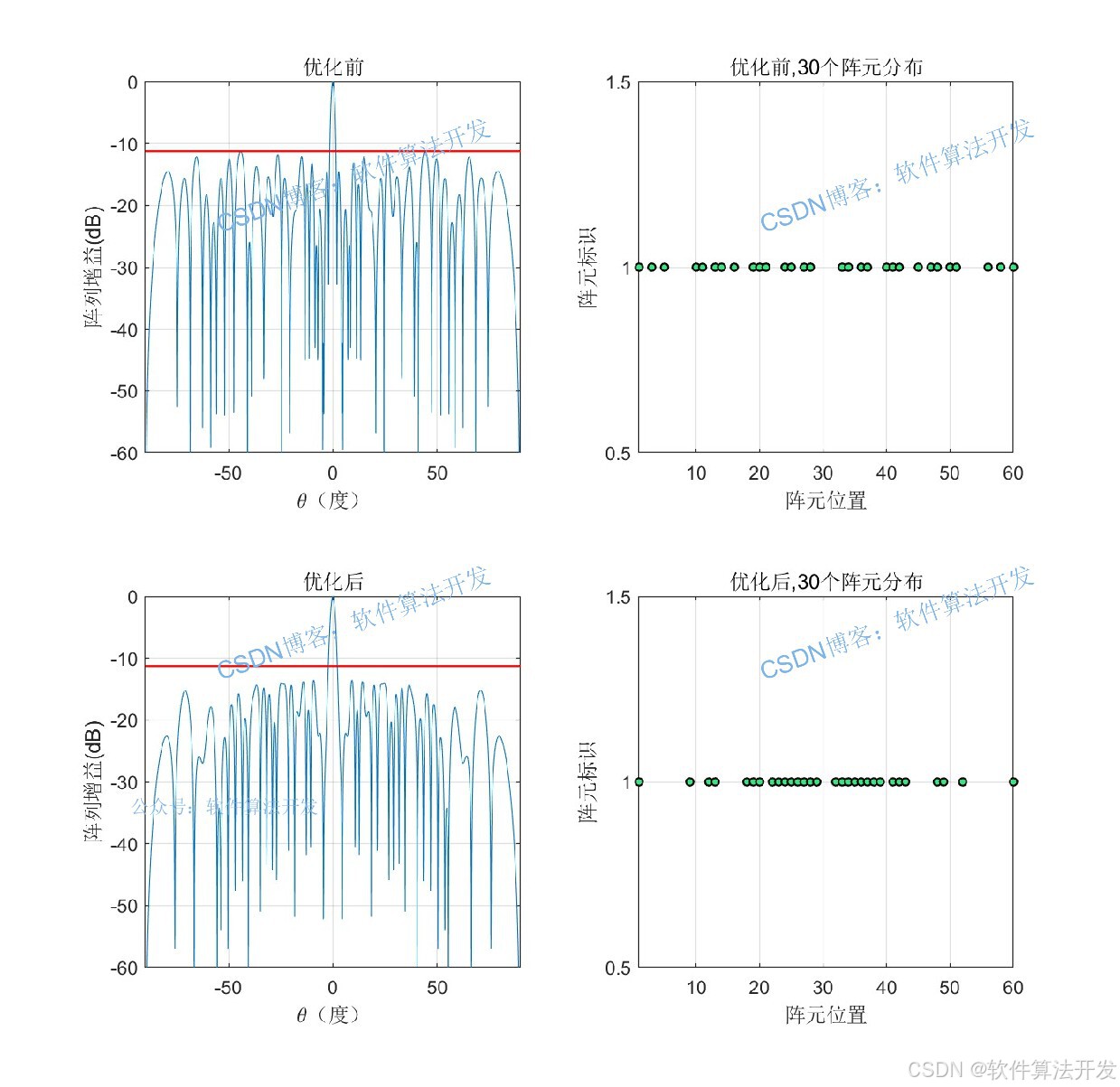
3.部分程序

...............................................................
load('R2.mat')
d = 0.5;                  
lamda = 1;                 
seta0 = 0*pi/180;        NN = 1800;                
%%%%%%%%%%%%%%%%%%%%%%%%%
seta = linspace(-pi/2,pi/2,NN);
for m = 1:NNfai = 2*pi*d/lamda*(0:(L-1))*(sin(seta(m))-sin(seta0));F1(m) = abs(sum(exp(sqrt(-1)*fai).*fBest'));  
end
FdB = 20*log10(F1/max(F1));subplot(223);
plot(seta*180/pi,FdB)
xlabel('\theta（度）')
ylabel('阵列增益(dB)')
grid on
axis([-90,90,-60,0])
hold onplot(seta*180/pi,LINES*ones(size(seta)),'r','LineWidth',1)title('优化后');
subplot(224);
plot(fBest,'bo',...'LineWidth',1,...'MarkerSize',4,...'MarkerEdgeColor','k',...'MarkerFaceColor',[0.2,0.9,0.5]);xlabel('阵元位置')
ylabel('阵元标识')
grid on
axis([1,L,0.5,1.5])
title(['优化后,',num2str(sum(fBest)),'个阵元分布']);
107

4.算法理论概述

阵列模型建立

设线阵沿x轴排列，总长度为L，阵元数量为N（N<<均匀线阵的阵元数，体现稀疏性）。第i个阵元的位置为x_i（0 ≤ x_i ≤ L），需满足x_i≠x_j（i≠j）。阵列在方位角θ处的归一化方向图为：

遗传算法编码

将阵元位置编码为染色体，采用实数编码方式：

染色体长度为N，每个基因对应一个阵元位置x_i；

约束条件：0≤xi≤L 且∣xi−xj∣≥dmin（dmin 为最小阵元间距，避免互耦过强，通常取λ/2）。

适应度函数设计

适应度函数用于评估染色体（阵元排布）的性能，目标是最小化副瓣电平。常见设计如下：

f=−PSLL

PSLL为当前排布的峰值副瓣电平（dB），取负值使副瓣越低，适应度越高；

稀疏线阵的核心挑战是在给定阵元数量（通常远小于均匀线阵）的情况下，通过调整阵元位置，使天线阵列的波束方向图满足预设性能指标（如副瓣电平、主瓣宽度、方向性系数等）。遗传算法（Genetic Algorithm, GA）通过模拟自然选择、交叉、变异等生物进化过程，在解空间中高效搜索最优阵元排布方案，其原理可概括为：