《Learning To Count Everything》论文阅读

论文地址：https://arxiv.org/abs/2104.08391
源码：https://github.com/cvlab-stonybrook/LearningToCountEverything

🖼️ 《当机器学会数星星：记一次对“万物可数”的温柔探索》

📘 第1节：引言（Introduction）

一、人类 vs. 机器：计数能力的巨大差距

人类非常擅长数东西：无论是书本、水果、玩具还是动物，我们看到就能数。但目前最先进的计算机视觉方法却只能处理少数几类物体，比如

• 人群计数（people）
• 车辆计数（cars）
• 细胞计数（cells）

🔍 深层含义：
计算机缺乏“通用计数”能力 —— 它不能像人一样“见物即数”

二、现有方法的两大瓶颈

作者指出，要实现通用视觉计数系统，面临两个根本性挑战

❌ 挑战一：依赖大量标注数据（Data Hunger）

大多数计数方法将计数视为全监督回归任务，需要数千张带标注的图像来训练一个全卷积网络，将输入图像映射到密度图（density map），再通过对密度图求和得到数量
🚫 后果：
很难扩展到上百种不同类别（如椅子、瓶子、书、玩具等），因为每一类都需要大量标注

❌ 挑战二：缺乏多类别数据集（Lack of Datasets）

目前流行的计数数据集大多只包含单一类别，例如：

• 人群计数：ShanghaiTech [55]、UCF-Crowd [16]
• 车辆计数：CARPK [14]、PUCPR+ [15]
• 细胞计数：BBBC [43

🚫 后果：
没有合适的基准数据集，就无法开发和评估“能数各种物体”的通用计数模型

✅ 解决方案：换个思路 + 新数据 + 新模型

为了突破这两个瓶颈，作者提出了一个全新的研究范式， 把计数变成“少样本回归任务

🎯 新任务设定（如 Fig. 1 所示）：

• 输入：一张图像 和 图像中几个样例物体的边界框（exemplar bounding boxes）
• 输出：该图像中所有与样例相似物体的总数

这更贴近人类的交互方式 —— 只需示范几个例子，就能完成计数

🔍 第2节：相关工作（Related Works）

本节主要从以下几个方面回顾了与“少样本视觉计数”相关的研究方向，并指出本文工作的定位与突破。

一、传统计数方法：专用模型 + 大量标注

📌 代表任务：

• 人群计数（Crowd Counting）：如 MCNN、CSRNet、PCC-Net 等；
• 车辆计数：停车场或交通监控中的车流统计；
• 生物医学图像分析：细胞、细菌、神经元计数；
• 农业应用：果实、害虫数量估计。

❗ 存在的问题：

• 依赖大量标注数据：每类物体都需要大量带标注的训练图像（如点标注或边界框）；
• 缺乏通用性：为“人”训练的模型不能直接用于数“苹果”；
• 标注成本高：尤其在医学、农业等领域，专家标注非常昂贵。

📌 结论：这些方法虽然在各自领域表现优异，但不适合通用、灵活的现实场景。

二、域自适应计数方法：缓解标注压力

原文提到：有些工作（如 [34]）尝试通过域自适应（Domain Adaptation）来减少目标域的标注需求。

✅ 做法：

• 在一个源域（source domain）上用大量数据训练计数模型；
• 然后用少量来自目标域（target domain）的标注样本微调或适配模型。

⚠️ 局限性：

• 仍然需要源域有海量标注数据；
• 如果源域和目标域差异大（比如从城市街道迁移到农场），效果会下降；
• 不支持完全新类别（如从未见过的物体类型）。

📌 所以这类方法只是“减轻”了标注负担，并未真正实现“通用计数”能力。

三、基于样例的匹配思想：FamNet 的灵感来源

原文指出：FamNet 的核心思想是利用查询图像与提供样例之间的强相似性。

🧩 相关工作1：自相似性（Self-Similarity）

• 提到 Shechtman 和 Irani 十多年前的工作 [41]，他们利用图像内部的重复结构（如纹理、图案）进行匹配和修复。
• FamNet 借鉴了这种“局部匹配”的思想，但不是图像内部匹配，而是样例与整图之间的跨区域匹配。

🧩 相关工作2：通用匹配网络 GMN [28]

• Lu 和 Zisserman 提出的 Generic Matching Network (GMN) 是一个类别无关的计数方法；
• 它使用视频跟踪数据预训练，学习如何根据几个样例去匹配同类物体；
• 支持“测试时适应”（test-time adaptation），即根据新图像中的样例调整模型行为。

⚠️ GMN 的局限：

需要几十到上百个样例才能有效适应；
如果没有足够的样例，对新类别的泛化能力很差；
如本文实验所示，GMN 在少样本（1~3个样例）下表现不佳。

📌 FamNet 的改进：

我们提出的方法可以在极少量样例（甚至1个）下高效工作，更适合真实用户交互场景。

四、少样本检测 vs. 少样本计数

原文强调：少样本检测（Few-Shot Detection）虽然相关，但与少样本计数有本质区别

对比维度	少样本检测（Few-Shot Detection）	少样本计数（This Work）
标注形式	需要边界框（bounding boxes）	只需点标注（dot annotations）
输出形式	检测框 + 类别标签	密度图 + 总数量
核心挑战	定位每个物体	估计整体分布
对遮挡的鲁棒性	差（遮挡导致漏检）	强（密度图可积分）
方法范式	先检测 → 再计数	直接预测密度图

🔍 关键洞察：

密度估计方法比“检测再计数”更鲁棒，尤其是在物体密集、重叠、遮挡严重的场景中。

原因在于：

• 检测方法必须做出“是否是一个物体”的二值化决策，容易出错；
• 密度估计保留了不确定性，通过积分得到总数，避免了逐个识别的误差累积。

📌 这也是为什么近年来人群计数、细胞计数等领域普遍采用密度估计的原因

✅ 总结：本文在相关工作中的定位

方向	本文的立场与创新
传统计数方法	❌ 太依赖数据和类别，不通用 → 我们提出通用框架
域自适应计数	⚠️ 仍需大量源域数据 → 我们完全摆脱对源域标注的依赖
GMN / 自相似匹配	✅ 借鉴其“样例驱动”思想 → 但我们支持更少样例、更强适应
少样本检测	❌ “检测+计数”不够鲁棒 → 我们采用密度估计范式
MAML / 元学习	✅ 借鉴“快速适应”机制 → 但我们简化训练，避免高阶梯度

📘 第3节：FamNet —— 少样本物体计数网络

一、整体目标

本节提出一个名为 FamNet（Few-shot Adaptation and Matching Network）的深度学习模型，用于解决少样本物体计数任务（Few-Shot Object Counting）：

给定一张图像和其中几个标注的样例物体（exemplar bounding boxes），模型要自动数出图中所有同类物体的数量，即使这个类别在训练时从未见过。

🎯 核心挑战：

• 模型必须具备跨类别泛化能力；
• 不能依赖预定义类别标签（如“人”、“车”）；
• 要通过“样例”来理解“我要数什么”。

🔧 3.1 网络架构（Network Architecture）

📈 整体流程（见 Fig. 2）

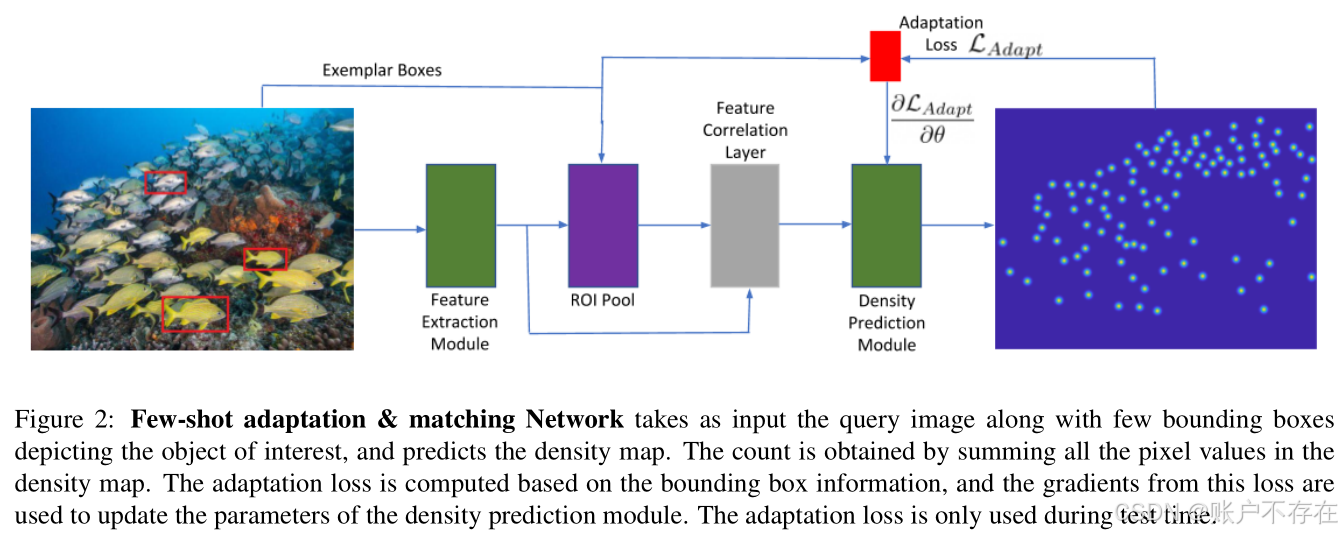
输入：- 图像 X ∈ ℝ^(H×W×3)- 若干个样例边界框（exemplar bounding boxes）输出：- 密度图 Z ∈ ℝ^(H×W) → 每个像素值表示该位置存在目标物体的概率密度- 最终计数 = 所有密度值之和：∑Z模型结构 = 特征提取模块 + 密度预测模块

✅ 模块1：多尺度特征提取（Multi-scale Feature Extraction）

使用的骨干网络：

• 预训练 ResNet-50（在 ImageNet 上训练过）；
• 只使用前四个卷积块（block1 ~ block4）；
• 这些层的参数在训练过程中冻结（frozen） → 不更新权重。

提取哪些特征？

从 block3 和 block4 的输出中提取特征图：

• block3：分辨率较高，适合小物体；
• block4：语义更强，适合大物体。

💡如何提取样例特征？

• 对每个样例边界框，使用 ROI Pooling（或 ROI Align）从 block3 和 block4 的特征图中裁剪并池化出固定大小的特征向量；
• 得到每个样例的“外观模板”（appearance template）。

这一步相当于：从图像中“剪下”样例区域，并提取其深层视觉特征。

✅ 模块2：密度预测模块（Density Prediction Module）

这是整个网络的核心创新点。

❌ 传统做法的问题：

如果直接把图像特征送入 CNN 预测密度图，模型会“记住”某些类别的特征（比如人的形状），无法泛化到新类别。

✅ FamNet 的解决方案：

不直接使用原始图像特征，而是使用“样例与图像之间的匹配响应图”作为输入。

具体步骤如下：

🔁 关键操作：相关性匹配（Correlation Matching）

• 缩放样例特征（Scale the exemplar features）：

  • 将样例特征分别缩放为原尺寸的 0.9×, 1.0×, 1.1×；
  • 目的是应对物体尺度变化（比如样例较小，但图中其他同类物体较大）。

• 计算相关图（Correlation Maps）：

  • 将每个尺度的样例特征，在整张图像的特征图上进行滑动窗口匹配（即互相关操作）；
  • 输出一个响应图（response map），表示每个位置与样例的相似度
  • 每个尺度产生一个相关图 → 共 3 个相关图。

  🧠 类比：就像用“模板”在整张图上做“模式搜索”，越像样例的地方响应越高。

• 拼接多尺度相关图：

  • 将三个尺度的相关图在通道维度上拼接（concatenate）；
  • 得到一个多通道的相关特征图，作为密度预测模块的输入。

🏗️ 密度预测模块结构

该模块是一个轻量级解码器（decoder），结构如下：

层	操作
Conv Block 1	卷积 + 激活
↑ Upsample	上采样（双线性插值）
Conv Block 2	卷积 + 激活
↑ Upsample	上采样
Conv Block 3	卷积 + 激活
↑ Upsample	上采样
Conv Block 4	卷积 + 激活
Conv Block 5	卷积 + 激活
Final Layer	1×1 卷积 → 输出单通道密度图 Z

✅ 输出密度图大小与输入图像一致（通过上采样恢复分辨率）

📚 3.2 训练方法（Training）

🎯 训练目标

最小化预测密度图$Z_{pred}$ 与真实密度图 $Z_{gt}$ 之间的 均方误差（MSE）
​

🧩 如何生成真实密度图 $Z_{gt}$？

这是关键步骤。真实标注是 点标注（每个物体中心一个点），但不能直接用点图监督，因为：

• 点是离散的；
• 模型输出是连续密度图。

✅ 标准做法：高斯核平滑（Gaussian Smoothing）技术

将每个点扩展为一个高斯峰，形成连续密度分布。

但传统方法（如人群计数）使用固定大小的高斯核（如 15×15），这在 FSC-147 上不行！

⚠️ 问题：物体尺度差异巨大！

FSC-147 包含：

• 小物体：回形针、豆子 → 高斯核要小；
• 大物体：椅子、箱子 → 高斯核要大。

如果统一用小核：

• 大物体重叠不足，变成多个峰；

如果统一用大核：

• 小物体模糊成一片，丢失细节。

✅ 解决方案：自适应高斯核（Adaptive Gaussian Smoothing）

步骤：

• 计算平均最近邻距离：
  • 对图像中每个标注点（物体中心），计算它到最近邻点的距离；
  • 取所有距离的平均值 → 记为 $d_{avg}$
• 设置高斯窗口大小：
  • 窗口大小 = $d_{avg}$
  • 高斯标准差 σ = $d_{avg}$ / 4

📌 物体越密集 → $d_{avg}$越小 → 高斯核越窄；
物体越稀疏 → $d_{avg}$越大 → 高斯核越宽。

示例：

一堆回形针：间距小 → 高斯核窄 → 每个针独立响应；
几把椅子：间距大 → 高斯核宽 → 每个椅子有一个明显峰值。

🛠 训练细节（Training Details）

参数	设置
优化器	Adam
学习率	$10^{-5}$
Batch Size	1（逐图训练）
图像预处理	缩放高度至 384，保持宽高比（aspect ratio）
特征提取器	ResNet-50 前四块，参数冻结
密度预测模块	随机初始化，端到端训练

🎯 为什么 batch size=1？

因为：

• 每张图像的物体类别、数量、尺度都不同；
• 图像尺寸各异（保持宽高比）；
• 很难批量对齐；
• 所以采用单图训练，更灵活。

✅ 总结：FamNet 的核心思想

模块	关键技术	目的
特征提取	冻结的 ResNet-50 + ROI Pooling	提取通用视觉特征
匹配机制	多尺度相关性计算	实现“样例驱动”的搜索
密度预测	基于相关图的轻量解码器	输出连续密度图
训练监督	自适应高斯核生成真值密度图	适配不同尺度物体
损失函数	像素级 MSE	监督密度图质量

📚 3.3 测试时自适应（Test-time Adaptation）

一、背景与目标

我们已经训练好了一个名为 FamNet 的物体计数网络。这个网络有两个关键特性：

• 不依赖具体类别（category-agnostic）：

  • 它不是为“人”或“车”专门设计的；
  • 而是学习一种通用能力：给定几个样例（exemplars），就能在图像中找出所有相似物体并计数。

• 样例（exemplar）的作用：

  • 用户提供几个带边界框的物体实例（比如圈出两只羊）；
  • 网络从中提取外观特征，作为“模板”去搜索整张图。

✅ 所以，FamNet 本身已经具备零样本/少样本计数能力。

❓ 问题：还能做得更好吗？

作者指出：目前只用了样例的外观信息，而样例的位置信息（即边界框的位置）还没有充分利用！

🎯 目标：在测试阶段，利用这些位置先验知识，进一步提升计数精度。

🔧 核心思想：测试时自适应（Test-time Adaptation, TTA）

• 在测试时，根据当前图像和提供的样例，临时调整模型或输出；
• 使用两个新的“损失函数”作为指导信号；
• 通过梯度下降进行微调，使预测更符合先验常识。

💡 这不是重新训练整个模型，而是“为这张图量身定制一次小优化”

🧩 关键定义

B： 用户提供的样例边界框集合；
b∈B： 其中一个样例框；
Z： FamNet 预测的密度图（density map），每个像素值表示该位置存在物体的“密度”；
$Z_b$： 从密度图 Z 中裁剪出的、位于边界框 b 区域内的子图（即这个区域的密度响应）
$||$Z_b$|{|}_1$ : $Z_b$ 中所有像素值之和 → 表示该区域内预测的物体数量。

✅ 损失函数 1：Min-Count Loss（最小计数损失）

🎯 动机：

每个样例边界框 b 内至少有一个真实物体，所以预测的密度总和不应小于 1。但不能强制等于 1，因为：

• 物体可能重叠；
• 边界框可能覆盖到邻近物体；
• 密度图是连续的，允许局部积分 >1。

📈 数学定义：

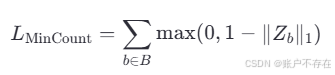
🧠 含义：

$||Z_b|{|}_1$ ：边界框 b 内密度值的总和
如果 $||Z_b|{|}_1$ < 1 , 说明预测不足，产生正损失；
如果 $||Z_b|{|}_1$ ≥ 1 , 则该项损失为0；

🛠 作用：

防止模型在已知有物体的位置上“低估”；
是一种软约束（soft constraint），鼓励模型尊重先验位置信息。

✅ 损失函数 2：Perturbation Loss（扰动损失）

🎯 动机来源：相关滤波跟踪算法（Correlation Filter Tracking）

• 在目标跟踪中，算法学习一个滤波器，使其在目标位置响应最大，在偏移位置响应逐渐降低（通常呈高斯分布）；
• 这样可以精确定位目标。

🤔 类比到计数任务：

• 密度图 Z 实际上就是样例模板与图像的匹配响应图（correlation response map）；
• 所以，在每个样例框 b 的中心，响应应该最高；
• 周围响应应平滑下降，理想形状是一个高斯峰

📈 数学定义：

设 $G_{h\times w}$ 是一个大小为 h×w 的二维高斯核（中心对齐，标准差适中），则：

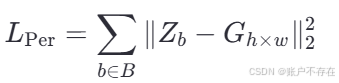
🧠 含义：

• ‖ $Z_b$ − $G_{h\times w}$||${}_2^2$ : 逐像素平方误差（MSE）；
• 衡量 $Z_b$ 是否接近理想高斯形状
• 强制模型在样例位置输出一个尖锐、集中、形状规则的响应峰

🛠 作用：

提升定位精度；
减少误检（多个响应峰）；
使密度图更符合物理意义。

🔗 组合损失：Adaptation Loss（自适应损失）

将两个损失加权组合，形成最终优化目标：

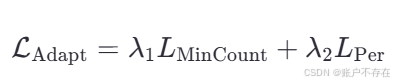
其中：
${\lambda }_1$ =$10^{-}9$
${\lambda }_2$ = $10^{-}4$
这些权重看起来非常小，但这是精心调参的结果

❓ 为什么权重这么小？为什么学习率这么低？

这是一个关键设计！

🎯 原因：保持损失尺度一致性

训练时使用的损失是全图像素级 MSE

数值通常在 $10^{-3}$ ~ $10^{-1}$ 量级, 而 $L_{MinCount}$ 和 $L_{per}$ 只作用于少数几个局部区域，原始值很小。
如果不加权或权重过大：

• 损失不平衡 → 某一项主导，破坏优化；
• 梯度太大 → 更新幅度过猛，偏离训练好的模型；
• 梯度太小 → 无法有效调整。
  ✅ 所以：
  调整 ${\lambda }_1$，${\lambda }_2$ 目的是让 $L_{Adapt}$ 的数值大小和梯度尺度与训练损失相近，确保优化过程温和而有效。

🚫 为什么训练时不使用这个损失？

作者明确指出：“Note that the adaptation loss is only used at test time.”

原因如下：

原因	说明
✅ 训练时监督更强	训练时已有全图密度图监督（MSE over all pixels），信息更丰富
❌ Adaptation Loss 监督较弱	它只关注几个样例框，无法提供全局学习信号
🔁 冗余性	在训练时加入这些损失不会带来明显提升，反而可能干扰收敛
🎯 分工明确	训练学“通用能力”，测试做“精细调整”

🌟 总结一句话

FamNet 在训练时学会“如何计数”，在测试时通过引入基于位置先验的自适应损失（Min-Count + Perturbation），进一步优化密度图，使其更符合“这里有物体”和“响应应集中”的常识，从而在新类别上实现更高精度的零样本计数。

📚 第4节：FSC-147 数据集详解

一、为什么需要一个新的数据集？

❓ 现有数据集的局限性

作者要训练一个用于少样本物体计数（Few-shot Object Counting）的模型 FamNet，但发现现有的公开数据集都不适合这个任务，原因如下：

问题	说明
🔹 类别单一	大多数计数数据集只关注特定类别，如：人群计数（ShanghaiTech, UCF-QNRF）、车辆计（CARPK）、细胞计数（BioCell）→ 不支持“新类别”的泛化能力评估
🔹 缺乏合适图像	多类别数据集（如 COCO）虽然类别多，但：每张图中同类物体数量少；同类物体姿态、外观差异大（比如不同角度的人）；不符合“密集、相似物体”的计数场景

✅ 所以：没有现成的数据集能支持“在新类别上用几个样例进行计数”这一任务。

✅ 解决方案：构建 FSC-147 数据集

作者团队自己收集并标注了一个全新的数据集：

名称	FSC-147（Few-Shot Counting - 147 categories）
图像总数	6,135 张
物体类别	147 个
总物体数	343,818 个
每图平均物体数	56 个
最少/最多物体数	7 ~ 3,701 个
应用场景	少样本计数、零样本计数、跨类别泛化

🎯 目标：让模型学会“给几个样例，就能数出任意新类别物体的数量”。

🧱 4.1 图像收集（Image Collection）

分两步进行：

1️⃣ 自动检索（Image Retrieval）

关键词搜索：对每个物体类别（如“pen”、“bottle”），使用搜索引擎抓取候选图像；
搜索平台：Flickr、Google、Bing；
工具：开源爬虫工具 [7, 45]；
优化查询词：添加描述数量的形容词，提高命中率：
如：“many pens”、“lots of books”、“stack of bricks”；
每类收集：300 ~ 3000 张候选图像。
🎯 目的是获取大量包含多个同类别物体的图像。

2️⃣ 人工筛选（Manual Verification and Filtering）

从自动抓取的图像中，人工筛选出符合以下标准的图像：

筛选条件	说明
✅ 高图像质量	分辨率足够高，能清晰区分各个物体
✅ 足够多的物体数量	每张图中目标物体 ≥ 7 个， 👉 因为人类不需要帮助数“1~6个”物体，重点是大规模计数
✅ 外观相似性	同类物体在姿态、纹理、颜色上较一致，👉 例如：整齐排列的笔、堆叠的乐高块 、👉 避免姿态差异太大的情况（如飞鸟、奔跑的人）
✅ 无严重遮挡	如果遮挡严重导致人也难以准确计数，则剔除

🎯 目的是确保图像适合“视觉计数任务”，避免歧义或噪声

📝 4.2 图像标注（Image Annotation）

每张图像由标注员使用 OpenCV 图像标注工具 进行标注，包含两种类型：

1️⃣ 点标注（Dot Annotation） → 用于生成密度图

每个物体实例在其近似中心位置打一个点；
用于后续生成密度图（density map），作为监督信号；
即使部分遮挡，只要可见部分 >10%，就应标注；
对于多类别图像，只标注一个选定的类别（避免混淆）。
📌 这是计数任务的标准标注方式，类似于 ShanghaiTech 等数据集。

2️⃣ 边界框标注（Bounding Box Annotation） → 用于提供“样例”

从每个图像中随机选择3个物体作为样例（exemplars）；
为这3个物体画出轴对齐的矩形边界框（axis-aligned bounding boxes）；
这些样例将在训练和测试时作为“模板”，告诉模型：“这是你要数的物体”。
🎯 目的是模拟真实应用场景：用户圈出几个样例，模型据此计数。

🔀 4.3 数据集划分（Dataset Split）

为了评估模型在新类别上的泛化能力，采用 “类别不重叠” 的划分方式：

集合	类别数	图像数	用途
训练集（Train）	89 类	3,659 张	训练 FamNet 模型
验证集（Validation）	29 类	1,286 张	调参、选择超参数（如 λ₁, λ₂）
测试集（Test）	29 类	1,190 张	评估在完全没见过的类别上的性能

✅ 关键点：训练时没见过测试类别的任何图像或样例 → 真正的“零样本”或“少样本”设置

📊 4.4 数据统计（Data Statistics）

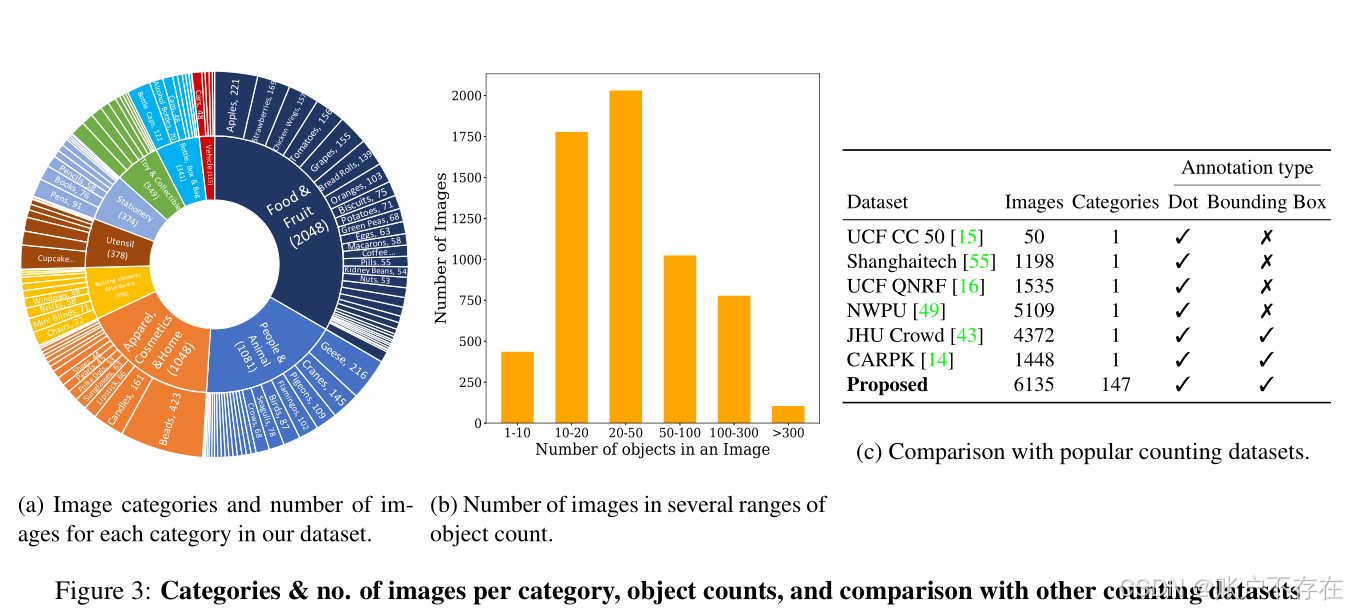
基本统计信息：

指标	数值
图像总数	6,135
平均图像尺寸	宽 938 px，高 774 px
平均每图物体数	56 个
最少物体数/图	7 个
最多物体数/图	3,701 个（原文写3731，后文说3701，应为笔误）
总物体数	343,818 个

按类别统计（极端情况）

类别	平均每图物体数	说明
🧱 最高
- Lego（乐高）	303	密集堆叠，外观高度一致
- Brick（砖块）	271	工地或仓库场景
- Marker（记号笔）	247	整齐排列的文具
📉 最低
- Supermarket shelf（超市货架）	8	商品种类多，同类数量少
- Meat Skewer（肉串）	8	每串肉块数少
- Oyster（生蚝）	11	分布稀疏

📈 图3b 是一个直方图，显示不同物体数量区间内的图像数量分布。

🌟 FSC-147 的核心特点总结

特性	说明
✅ 多样性高	147 个类别，涵盖文具、厨具、食品、动物、车辆等
✅ 规模大	超6千张图像，34万+标注点
✅ 适合少样本计数	每图提供3个样例框，支持 exemplar-based learning
✅ 真实场景导向	图像来自网络，非实验室环境
✅ 评估公平	类别不重叠划分，真正测试跨类别泛化能力

🧠 为什么这个数据集重要？

FSC-147 是首个专门为 Few-shot Counting 设计的大规模数据集，它的出现填补了以下空白：

之前缺失的能力	FSC-147 提供
跨类别泛化计数	✅ 支持训练在 A 类，测试在 B 类
样例引导计数	✅ 提供 exemplar bounding boxes
密集相似物体计数	✅ 筛选了高密度、低变化的图像
公平 benchmark	✅ 明确划分 train/val/test 类别

📌 它不仅服务于本文的 FamNet，也为后续研究提供了标准 benchmark

🖼️ 示例图示意（Fig. 4）

红点 ●：每个物体的中心标注；
蓝色方框 [ ]：三个随机选中的样例，供模型学习外观
注意：FSC-147 数据集中，每张图像只标注一个物体类别。用户通过提供样例来指定：“我要数的是这种物体”，模型只需关注这一类。

✅ 总结一句话

FSC-147 是一个专为少样本物体计数设计的大规模数据集，包含 147 类、6,135 张图像，每图标注了物体中心点和 3 个样例边界框，并采用类别不重叠的划分方式，支持模型在新类别上的零样本/少样本计数能力评估。

🧪 第5节 实验详解：FamNet 的全面评估

5.1 性能评估指标（Performance Evaluation Metrics）

为了衡量计数方法的准确性，作者使用了两个经典指标：
MAE（Mean Absolute Error）平均绝对误差

• 定义：MAE是所有预测值与真实值之间绝对差值的平均值
• 公式
  
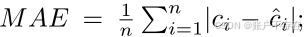
  RMSE（Root Mean Squared Error）均方根误差
• 定义：RMSE是所有预测值与真实值之间差值平方的平均值的平方根
• 公式
  

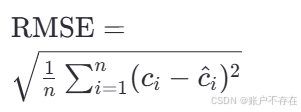
📌 说明：

n：测试图像数量；
$C_i$ : 第 i 张图的真实物体数量；
$\widehat{C_i}$ : 模型预测的数量
这两个指标广泛用于人群计数、物体计数等任务，能有效反映模型的整体精度和稳定性。

5.2 与少样本方法的对比（Comparison with Few-Shot Approaches）

作者将 FamNet 与其他6种方法进行比较

✅ 对比方法包括：

类型	方法	说明
基线方法（Baseline）	1. 输出训练集平均数量 ；2. 输出训练集中位数	非常简单的策略，作为下限参考
少样本检测器改编	[8], [17] 提出的先进少样本检测器	“先检测再数”范式
少样本匹配模型	GMN（Generic Matching Network）[28]	类别无关的匹配网络
元学习方法	MAML（Model-Agnostic Meta Learning）[9]	经典元学习框架，支持快速适应新任务

🔧 所有方法都在 FSC-147 训练集上重新训练或微调，确保公平比较。

🔍 关键发现（见 Table 1）：

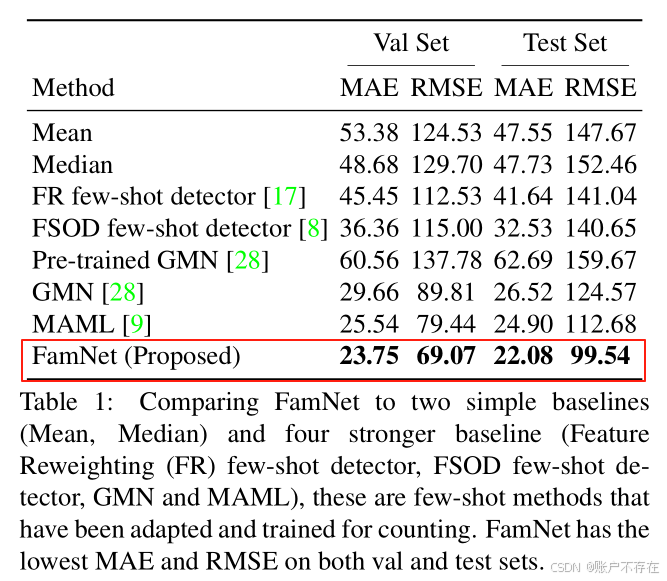
结论	详细解释
✅ FamNet 表现最优	在 MAE 和 RMSE 上均显著优于其他所有方法。
⚠️ GMN 效果差	即使是专为通用计数设计的 GMN，预训练版本效果很差；但在 FSC-147 上训练后性能提升 → 说明 FSC-147 数据集本身的价值。
❌ 少样本检测器表现不佳	即使使用最先进的检测器（如 [8][17]），也远不如密度估计方法。
✅ MAML 是次优方法	因为它结合了元学习 + 密度估计结构，表现不错，但仍不如 FamNet。
⏱️ FamNet 训练更快	比 MAML 快约3倍，因为 MAML 需要计算高阶梯度（二阶梯度），而 FamNet 不需要

📌 重要结论：

“先检测再计数”（detection-then-counting）的方式在通用物体计数任务中不如“直接密度估计”方式有效。

这其实在人群计数领域早已被证实（如 CSRNet、MCNN 等），但本文首次在通用物体计数场景下验证了这一点。

原因在于：

• 密度估计避免了二值化决策（是否是一个物体）；
• 更鲁棒地处理遮挡、重叠、尺度变化等问题；
• 不依赖边界框精确定位。

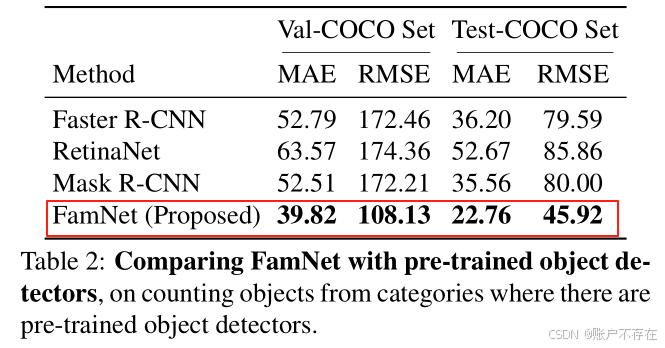
5.3 与目标检测器的对比（Comparison with Object Detectors）

有些人可能会想：“能不能直接用现成的目标检测器来数物体？”

作者也做了这个实验。

实验设置：

• 选取 COCO 数据集中有预训练模型的类别（如人、车、椅子等）；
• 构建两个子集：Val-COCO（277张图）和 Test-COCO（282张图）；
• 使用 Detectron2 库中的主流检测器：
  • Faster R-CNN
  • Mask R-CNN
  • RetinaNet
• 所有检测器都在 COCO 上用数千张标注图像训练过

实验结果（Table 2）：

❗ FamNet 在这些类别上仍然优于所有预训练检测器！

🤯 为什么？

尽管检测器在 COCO 上训练充分，但在 FSC-147 的真实场景中存在以下问题：

• 物体尺度变化大；
• 背景复杂；
• 检测器对未见姿态/光照敏感；
• 少样本场景下无法微调。

而 FamNet 通过样例驱动的匹配机制，能更灵活适应新图像中的具体实例。

📌 结论：对于通用、灵活的计数任务，专用检测器未必比通用密度估计方法更强

5.4 消融实验（Ablation Studies）

消融实验用于分析模型各个组件的重要性。

实验一：样例数量的影响（Table 3）

样例数	MAE
1	4.7
2	3.9
3	3.5

✅ 结论：

• 即使只有 1个样例，FamNet 也能工作；
• 有 2个样例 时，性能已超过 Table 1 中所有竞争方法；
• 样例越多，性能越好 → 用户可通过提供更多样例获得更准确结果。

💡 实用意义：用户交互友好，支持“从粗到精”的计数体验。

实验二：关键组件的重要性（Table 4）

作者移除以下组件进行对比

组件	作用	移除后影响
多尺度图像特征	捕捉不同分辨率下的物体	性能下降
多尺度样例特征	匹配不同大小的同类物体	性能下降
测试时适应（Test-time Adaptation）	利用样例位置优化密度图	显著下降

✅ 结论：

• 所有三个组件都至关重要；
• 每增加一个组件，性能稳步提升；
• 特别是“测试时适应”带来了显著增益。

🔍 回顾：测试时适应通过两个损失函数优化密度图：

• Min-Count Loss：保证每个样例区域内至少有一个物体；
• Perturbation Loss：让样例周围密度分布像高斯峰，提升定位精度。

5.5 特定类别计数能力测试（Counting Category-Specific Objects）

虽然 FamNet 是为通用计数设计的，但它也能用于特定类别任务。

实验任务：在 CARPK 数据集上数汽车

• CARPK：航拍停车场图像，共 989 张训练图 + 459 张测试图；
• 包含约 9 万个汽车实例；
• 是专门用于车辆计数的数据集。

对比方法：

方法	训练方式
FamNet–	在 FSC-147 上预训练，未见过 CARPK 数据
FamNet+	在 CARPK 训练集上微调，使用随机选的 12 个样例作为固定 exemplar

实验结果（Table 5）：

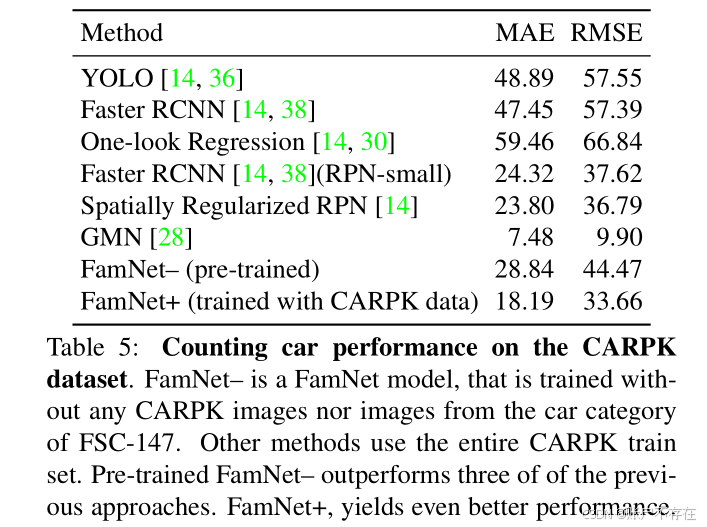
• FamNet+ 表现优异，仅次于 GMN；
• GMN 之所以更强，是因为它额外使用了 ILSVRC 视频数据集中的汽车视频序列进行训练 → 数据优势，非模型优势。

📌 结论：

即使不是为特定类别设计，FamNet 也能通过简单微调，在专业数据集上达到接近最优的性能。

5.6 定性结果分析（Qualitative Results）

Fig. 5：成功与失败案例

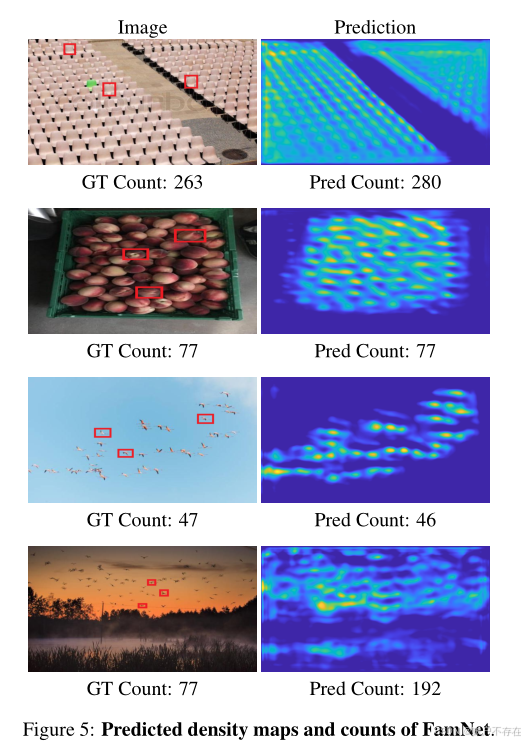
• 前3张图：成功案例
  • 密度图准确反映了物体分布；
  • 计数接近真实值。
• 第4张图：失败案例
  • 背景中某些区域与目标物体外观相似（例如纹理、颜色）；
  • 模型误把这些区域识别为前景物体；
  • 导致过估计（overcounting）。

💡 说明模型仍依赖外观匹配，对语义混淆敏感。

Fig. 6：测试时适应的效果可视化

• 展示了一个典型例子：测试时适应如何改进初始预测。
• 初始密度图在密集区域响应过高（可能因为多个物体靠近）；
• 经过$L_{Adapt}$ 优化后，模型自动降低密集区域的密度值，使其更符合实际分布；
• 最终计数更准确。

📌 意义：证明了测试时适应不仅能提升数值指标，还能物理意义上修正密度图的不合理分布。

✅ 总结：FamNet 的核心优势

优势	说明
通用性强	可处理 147 类不同物体，无需重新训练
仅需少量样例	1~3 个样例即可工作，交互友好
优于检测方法	在通用计数任务中，密度估计优于“检测+计数”
优于元学习方法	性能更高、训练更快（无需高阶梯度）
支持测试时优化	利用样例位置信息微调密度图，提升精度
可迁移到专业任务	稍作微调即可用于车辆计数等特定任务

🎯 总体结论

FamNet 是首个专为“少样本通用物体计数”设计的端到端可训练框架，结合多尺度匹配、密度估计和测试时适应机制，在多个基准上实现了最优性能，且具有良好的实用性与扩展性。

📌 第6节：结论（Conclusions）

这篇论文的核心思想和贡献在最后一节得到了高度凝练。作者通过提出一个新的任务范式、构建一个新数据集、设计一个创新模型，系统性地解决了“少样本视觉计数”这一具有挑战性的任务。

🧩 第7节：快速推理

打开源码的 demo.py 脚本，修改以下三个参数即可快速推理

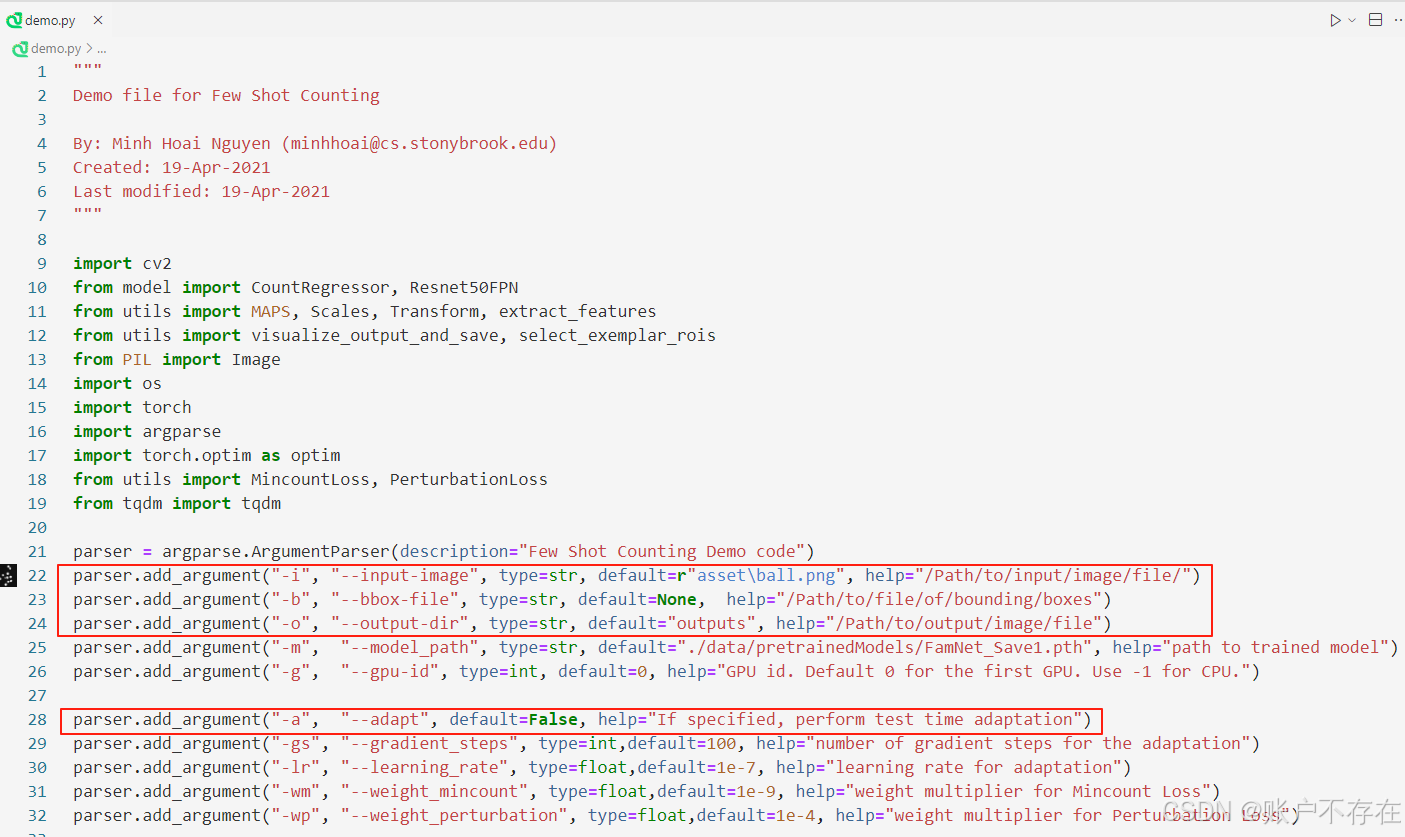
• 如果 --bbox-file 为 None，表示手动标注示例框（交互模式）， 程序会弹出窗口允许手动框选目标示例

  • 按n键：拖动鼠标绘制示例框
  • 按 ‘space’（空格键） ：保存当前标注
  • 按q或Esc：退出程序

  🎮 使用流程示例：

  运行 python demo.py 后，弹出一张图片；
  按 n 键；
  用鼠标在图中某个物体（如一个人、一个苹果）周围拖拽画框；
  松开鼠标后，按空格键保存当前示例；
  可重复按 n + 拖拽画框，添加更多样例；
  按 q 退出。

• 从文件加载示例框，若已提前用文本文件记录示例框坐标（格式：y1 x1 y2 x2，每行一个框），则 --bbox-file 直接传入文件路径

• –adapt 默认为False，表示不启用测试时自适应策略，否则，使用测试时适应策略，通过两个损失函数（Min-Count Loss + Perturbation Loss）优化密度图：

结果展示