《P6464 [传智杯 #2 决赛] 传送门》
题目描述
传智专修学院里有 n 栋教学楼,有 m 条双向通行道路连接这些教学楼,不存在重边和自环。每条道路都有一定的长度,而且所有教学楼之间都可以直接或者间接的通过道路到达。我们可以很容易的求出这些教学楼之间的最短路。
为了使交通更为顺畅,校方决定在两个教学楼里增设一对传送门。传送门可以将这对教学楼的距离直接缩短为 0。利用传送门,某些教学楼之间的最短路的距离就变短了。
由于预算有限,学校里只能安装一对传送门。但是校长希望尽可能方便学生,使任意两点之间的最短路长度的总和最小。当然啦,从 x 教学楼到 y 教学楼的长度和从 y 教学楼到 x 教学楼的长度只需要统计一次就可以了。
输入格式
输入第 1 行两个正整数 n,m(n≤100,m≤21n(n−1)),代表教学楼和道路数量。
接下来 m 行,每行三个正整数 xi,yi,wi(0<wi≤104),表示在教学楼 xi 和 yi 之间,有一条长度为 wi 的道路。
输出格式
输出一行,在最优方案下的任意点对的最短道路之和。
输入输出样例
输入 #1复制
4 5 1 2 3 1 3 6 2 3 4 2 4 7 3 4 2
输出 #1复制
14
说明/提示
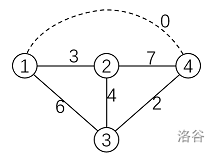
样例如图。当在 1 和 4 号教学楼架设一对传送门时,1 → 2 的最短路是 3,1 → 3 的最短路是 0+2,1 → 4 的最短路是 0,2 → 3 的最短路是 4,2 → 4 的最短路是 3+0,3 → 4 的最短路是 2,最短路之和是 14,是最佳方案。
代码实现:
#include <iostream>
#include <cstring>
#include <limits.h>
using namespace std;
// 地图数组:存储两点之间的距离
int distanceMap[101][101];
// 保存初始地图状态的数组
int originalDistanceMap[101][101];
// 节点数量和边数量
int nodeCount, edgeCount;
// 用于存储最小总距离的变量
int minTotalDistance = INT_MAX;
int main()
{
ios::sync_with_stdio(0);
cin >> nodeCount >> edgeCount;
// 初始化所有路径为一个较大的值(表示无穷远)
memset(distanceMap, 0x3f, sizeof(distanceMap));
// 读取边的信息并填充地图
for (register int i = 1; i <= edgeCount; ++i)
{
int startNode, endNode, weight;
cin >> startNode >> endNode >> weight;
distanceMap[startNode][endNode] = weight;
distanceMap[endNode][startNode] = weight;
}
// 执行Floyd算法计算所有点对之间的最短路径(无传送门时)
for (int intermediate = 1; intermediate <= nodeCount; ++intermediate)
for (int start = 1; start <= nodeCount; ++start)
for (register int end = 1; end <= nodeCount; ++end)
{
if (distanceMap[start][end] > distanceMap[start][intermediate] + distanceMap[intermediate][end])
{
distanceMap[start][end] = distanceMap[start][intermediate] + distanceMap[intermediate][end];
}
// 保存初始的最短路径状态
originalDistanceMap[start][end] = distanceMap[start][end];
}
// 尝试所有可能的两个节点作为传送门
for (int portalA = 1; portalA <= nodeCount; ++portalA)
for (int portalB = 1; portalB < portalA; ++portalB)
{
// 设置传送门:两点之间的距离为0
distanceMap[portalA][portalB] = 0;
distanceMap[portalB][portalA] = 0;
// 以portalA为中间节点更新最短路径
for (int start = 1; start <= nodeCount; ++start)
for (register int end = 1; end <= nodeCount; ++end)
{
if (distanceMap[start][end] > distanceMap[start][portalA] + distanceMap[portalA][end])
{
distanceMap[start][end] = distanceMap[start][portalA] + distanceMap[portalA][end];
}
}
// 以portalB为中间节点更新最短路径
for (int start = 1; start <= nodeCount; ++start)
for (register int end = 1; end <= nodeCount; ++end)
{
if (distanceMap[start][end] > distanceMap[start][portalB] + distanceMap[portalB][end])
{
distanceMap[start][end] = distanceMap[start][portalB] + distanceMap[portalB][end];
}
}
// 计算所有点对之间的总距离
int currentTotal = 0;
for (int start = 1; start <= nodeCount; ++start)
for (register int end = 1; end < start; ++end)
{
currentTotal += distanceMap[start][end];
}
// 更新最小总距离
if (currentTotal < minTotalDistance)
{
minTotalDistance = currentTotal;
}
// 恢复地图到初始状态,为下一次迭代做准备
for (int start = 1; start <= nodeCount; ++start)
for (register int end = 1; end <= nodeCount; ++end)
{
distanceMap[start][end] = originalDistanceMap[start][end];
}
}
// 输出最小的总距离
cout << minTotalDistance;
return 0;
}
