算法解决爬楼梯问题

我们先来看题：一个 n 级长的楼梯，每次有两种爬法，一种是一次爬一级，另一种是一次爬两级，那么在长度会变化的情况下，我们总共有多少中爬楼梯方法呢？

如下图内容：

这个是一个非常容易的题目，通过观察我们会发现如下规律：

一个人到达第 i 层楼底包括两种方法：

1. 选择从第 i-1 层再爬 1 步
2. 选择从第 i-2 层再爬 2 步

然后一步步递推下来便是：

如果用 f[i] 表示达到第 i 层楼梯的所有方法，那么它进一步等于到达第 i-1 层楼梯的方法加上到达第 i-2 层楼梯的方法的和，即

f[i] = f[i-1] + f[i-2]

所以，直接递归就可以完成题目的要求啦，这个程序非常简单，但是如果直接递归的话对于力扣的题目而言会 TLE（超时），此时我们需要使用迭代的方法：

class Solution {public:int climbStairs(int n) {int prev = 0;int cur = 1;for(int i = 1; i <= n ; ++i){int tmp = cur;cur += prev;prev = tmp;}return cur;}
};

由于这个题目非常具有特色，我们在计算了少量的楼梯个数后会发现，这个方法数是符合斐波那契数列的值的：

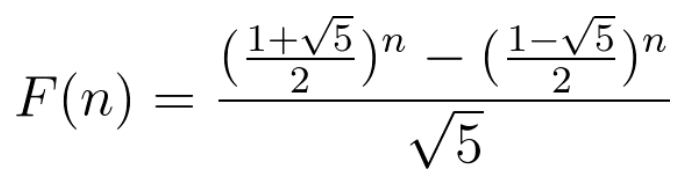
所以我们可以进一步想到通过通项公式的方法得出题解：

class Solution {public:int climbStairs(int n) {const double s = sqrt(5);return floor((pow((1+s)/2, n+1) + pow((1-s)/2, n+1))/s + 0.5);}
};