当前位置：首页 > news >正文

【详细证明 | 题解】洛谷 P2508 [HAOI2008] 圆上的整点 [数学]

news 2025/10/15 12:43:56

【官方双语】隐藏在素数规律中的π_哔哩哔哩_bilibili

先去看一遍，大概知道怎么做就可以。

不用全看懂，因为视频本身也没有很详细。

P2508 [HAOI2008] 圆上的整点 - 洛谷 (luogu.com.cn)

前置知识：

复平面

1.复平面与高斯整数

复平面（Complex plane），是几何表示复数的一种方式。

我们常见的数轴，是一条由原点向左（负）右（正）两端无限延伸的直线。

你可以想成：数轴正方向端乘以 $-1$ ，就逆时针调转了 $180^{\circ}$ ，变成了负方向端。

而 $i=\sqrt{-1}$ ，就相当于正方向端只逆时针转了 $90^{\circ}$ ，变成了一条竖着的轴。

把负方向端也逆时针转 $90^{\circ}$ ，就组成了复平面。

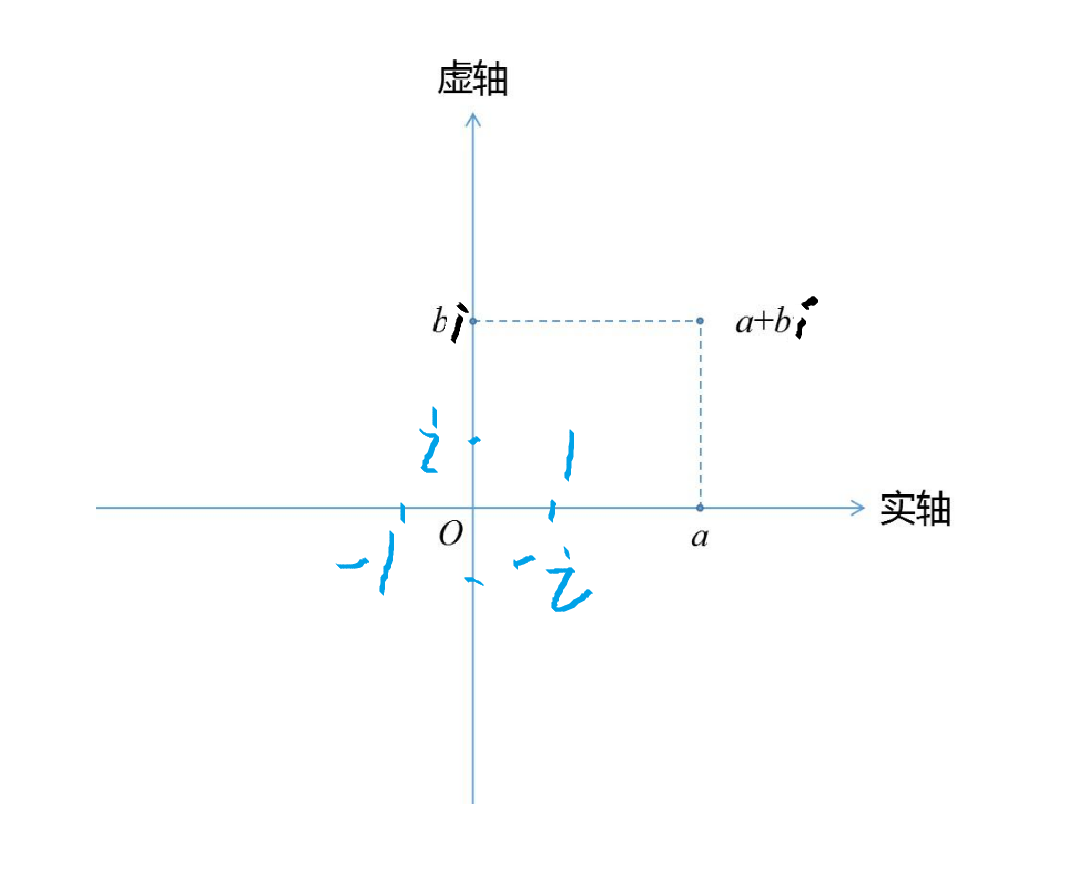
这个平面上的每个数都可以写成 $a+bi$ ，其中 $a$ 是实部， $b$ 是虚部。

是卡尔·弗里德里希·高斯（Carl Friedrich Gauss）第一个系统化复数和提出复平面，

所以我们也把复平面叫做高斯平面。

其中 $a,b$ 都是整数的形如 $a+bi$ 的复数叫做高斯整数，

这些高斯整数 $z=a+bi$ ，与它的复共轭 $\bar{z}=a-bi$ 的乘积是一个平方和 $a^2+b^2$ 。

（复共轭：原数实部不变，将虚部变号得到的数）

而高斯素数，是高斯整数中的特例。

高斯素数定义：一个无法分解成两个非单位高斯整数的积的高斯整数。

我们设 $N(z)=z*\bar{z}$ 为 $z$ 的范数，即该高斯整数与其复共轭的积。

且当 $z$ 为高斯整数， $N(z)=z*\bar{z}$ 一定是非负整数。

范数有如下性质： $N(zw)=N(z)N(w)$

证明：

设 $z=a+bi,w=x+yi$ ，

$N((a+bi)*(x+yi))=(a^2+b^2)*(x^2+y^2)$

$N((ax-by)+(ay+bx)i)=(a^2+b^2)*(x^2+y^2)$

$(ax-by)^2+(ay+bx)^2=(a^2+b^2)*(x^2+y^2)$

$ax^2+ay^2+bx^2+by^2=ax^2+ay^2+bx^2+by^2$

得证。

高斯整数是整数 $(b=0)$ 时，只有形如 $p\equiv 3(mod\ 4)$ 的奇素数 $p$ ，是高斯素数。

反证：

假设 $p\equiv 3(mod\ 4)$ 的奇素数 $p=\alpha \beta$ （即两个非单位高斯整数的积）。

则有： $N(p)=p^2=N(\alpha )N(\beta )$

因为 $p$ 是质数，而 $\alpha ,\beta$ 是非单位高斯整数，所以：

$p=N(\alpha )=N(\beta )$

但 $p\equiv 3(mod\ 4)$ 的奇素数无法分成两个平方和，

（详见【数学】费马平方和定理证明 [简洁版]-CSDN博客的最后附节）

也就无法分解成一个高斯整数与其复共轭的积。

所以 $p\neq N(\alpha )\neq N(\beta )$ ， $p\neq \alpha \beta$ ，证毕。

我们还发现，当高斯整数 $z$ 与其复共轭的积是一个 $p\equiv 1(mod\ 4)$ 的奇素数时，

这个高斯整数 $z$ 也无法分解成两个非单位高斯整数的积，是高斯素数。

（而且这个高斯素数 $z$ 对于每个 $p\equiv 1(mod\ 4)$ 是唯一的（ $0<a<b$ 的形式），

详细证明请看上面“费马平方和定理证明”的链接）

反证：

假设这个高斯整数 $z$ 可以分解成 $z=\alpha\beta$ ，则有：

$p=N(z)=N(\alpha )N(\beta )$

又因为 $\alpha ,\beta$ 是非单位高斯整数，所以 $N(\alpha )\neq 1,N(\beta )\neq 1$ 。

而 $p$ 是质数，不可能分解成两个非负非 $1$ 整数的乘积。

所以高斯整数 $z$ 无法分解成两个非单位高斯整数的积，是高斯素数。

之前我们提到的都是奇素数，那 $2$ 呢？

$2$ 能分解成 $(1+i)(1-i)$ ，很明显这俩都是高斯整数且是高斯素数。

记住这俩特殊的就行。

2.高斯素数和圆

如果一个正整数 $n$ ，是一个高斯整数的范数，那么这个正整数就能被分解成两个平方和。

更细致的想一下，这个正整数 $n$ 能分成几种不同的共轭对乘积，

那么这个正整数 $n$ 就能被分解成几对平方和，

半径为 $n$ 的圆上就有几个整点。

就像每个正整数 $n$ 都有唯一质数分解一样，每个正整数 $n$ 都有唯一高斯素数分解 $(0<a<b)$ 。

（唯一性证明：【数学】费马平方和定理证明 [简洁版]-CSDN博客）

比如 $5$ 的高斯素数分解就是： $(1+2i)(1-2i)$

（如果不要求 $(0<a<b)$ 那么 $(2+i)(2-i)$ 、 $(-1-2i)(-1+2i)$

和 $(-2-i)(-2+i)$ 也算，但肯定没有别的了）

$8$ 的高斯素数分解是： $(1-i)^3(1+i)^3$

$19$ 自己本身就是高斯素数。

我们如果把 $n$ 分解成高斯素数，再统计这些高斯素数能分成多少对共轭对，就得到答案。

一个个来看，假设枚举到当前高斯素数 $p$ 。

（1）它的共轭 $\bar{p}$ 不是它本身， $n$ 里有 $k$ 对 $p$ 和 $\bar{p}$ 。

那么这个 $2k$ 个高斯素数，要平均的分配到两块里，不然就组不成共轭。

为什么这么说？假设 $p=a+bi$ ，那么现在 $n$ 就有 $k$ 个 $(a+bi)$ ， $k$ 个 $(a-bi)$ 。

假设左边分到了 $r(0\leq r\leq k)$ 个 $(a-bi)$ ，右边分到了 $k-r$ 个 $(a-bi)$ 。

因为两边各有 $k$ 个数，左边和右边 $bi$ 的符号是相反的，所以最后结果乘积虚部也是相反数。

即左右共轭。

这就告诉我们，对于每个 $mod\ 4= 1$ 的质数，在 $n$ 里有 $k$ 个，我们都有 $k+1$ 种合法选法。

（2）它的共轭 $\bar{p}$ 是它本身， $n$ 里有 $k$ 个 $p$ 。

显然 $p\equiv 3(mod\ 4)$ ，且 $k$ 必须是 $2$ 的倍数，不然凑不出共轭。

选法就只有一种，那就是每边 $k/2$ 个。

最后所有选法要按乘法原理乘起来，同时因为我们严格要求了 $(0<a<b)$ ，

答案肯定不止算出来的乘积，那该怎么办呢？

想想 $5$ 的高斯素数分解：

$(1+2i)(1-2i)$ 、 $(2+i)(2-i)$ 、 $(-1-2i)(-1+2i)$ 和 $(-2-i)(-2+i)$ 。

后面的三个分别是由第一个 $*(-i),*(-1),*i$ 得来的。

所以在得出答案后还得 $*4$ ，这样才能不遗漏复平面上四个象限的点。

（可以看视频【官方双语】隐藏在素数规律中的π_哔哩哔哩_bilibili 里面，该知识点部分有动画）

但 $2$ 是特殊的， $(1-i)$ 和 $(1+i)$ 的关系本身就是 $*i$ 得来的。

这就导致了当 $n$ 里面有 $2$ 时，两个共轭之间是 $i$ 的倍数的关系，

这时候再去 $*(-i),*(-1),*i$ ，就会重复。

你可以把每次乘 $*1,*(-i),*(-1),*i$ 看作是将答案旋转 $90^{\circ}$ ，

而 $2$ 的 $(1-i)$ 和 $(1+i)$ 本身就一个差另一个 $90^{\circ}$ ，

再转就会重复。

好比 $10=2*5=(1+i)(1-i)(1+2i)(1-2i)$ ，

分配时，有四种选择，我们每次都取左边的作为答案：

$(1+i)(1+2i)|(1-i)(1-2i)=(1+3i),(1-3i)$

$(1+i)(1-2i)|(1-i)(1+2i)=(3-i),(3+i)$

$(1-i)(1+2i)|(1+i)(1-2i)=(3+i),(3-i)$

$(1-i)(1-2i)|(1+i)(1+2i)=(1-3i),(1+3i)$

可以发现， $(3-i),(3+i)$ 乘以 $i$ ，正好就是 $(1-3i),(1+3i)$ ，重复了。

我们之前遇到 $2$ ，因为有一对共轭，可以左右交换着来，所以答案是 $*2$ 的。

而现在又发现 $2$ 会导致最终答案的的一半失效，干脆遇到 $2$ 就不乘了。

最后再总结下质因数分解的规矩：

（1）遇到 $p\equiv 1(mod\ 4)$ 的奇质数， $n$ 里含多少个答案就乘以（多少个 + 1）。

（2）遇到 $p\equiv 3(mod\ 4)$ 的奇质数， $n$ 里含 $k$ 个， $k$ 必须是 $2$ 的倍数，

不然就没有合法答案。

（3）遇到 $2$ 不管。

（4）最后乘以 $4$ 。

有小朋友就会问了，这样真的能包含到全部的答案吗？

那些坐标上含有 $0$ 的呢，我们不是要求 $(0<a<b)$ ，能算到吗？

我们只是要求高斯素数在复数情况下是这样，最后分成的两块可没说。

比如 $25=(1+2i)(1-2i)(1+2i)(1-2i)$ ，当左右两边都分到 $1$ 个 $(1-2i)$ 时，

左右两边都是 $5$ ，这代表着 $5+0i=(5,0)$ ，再乘以 $4$ 就覆盖全部了。

3.本题及代码

我们前面讨论的正整数 $n$ 是直接等于平方和的，但现在题目是 $r^2=x^2+y^2$ 。

那简单，改一下规则，分解 $r$ 的质因数：

（1）遇到 $p\equiv 1(mod\ 4)$ 的奇质数， $r$ 里含多少个答案就乘以（2 * 多少个 + 1）。

（2）遇到 $p\equiv 3(mod\ 4)$ 的奇质数，不管，因为 $r^2$ 必然含有偶数个 $p$ 。

（3）遇到 $2$ 不管。

（4）最后乘以 $4$ 。

#include<bits/stdc++.h>
using namespace std;typedef long long LL;int main () {ios::sync_with_stdio(false);cin.tie(0);LL r, ans = 1; cin >> r;for (LL i = 2; i * i <= r; i ++) {   // 要除以质数，其他合数因为在比它小的质数时，就已经除以完了，不会管 int cnt = 0;while (r % i == 0) {r /= i;cnt ++;}if (i % 4 == 1) {ans *= (2 * cnt + 1);}}if (r != 1 && r % 4 == 1) {   // 没除以完，比如说 r 本身就是质数 ans *= 3;} cout << ans * 4 << "\n";return 0;
}

查看全文

http://www.dtcms.com/a/483576.html