机器学习 朴素贝叶斯
目录
一.什么是朴素贝叶斯
1.1 从 “概率” 到 “分类”
二.朴素贝叶斯的数学基础:贝叶斯定理
2.1 贝叶斯定理公式
2.2 从贝叶斯定理到朴素贝叶斯分类
2.3 “朴素” 的关键:特征独立性假设
三、朴素贝叶斯的三种常见类型
3.1 高斯朴素贝叶斯(Gaussian Naive Bayes)
3.2 多项式朴素贝叶斯(Multinomial Naive Bayes)
3.3 伯努利朴素贝叶斯(Bernoulli Naive Bayes)
四、朴素贝叶斯的工作流程
步骤 1:数据准备与预处理
步骤 2:计算先验概率P(C)
步骤 3:计算似然概率P(x_i|C)
步骤 4:预测新样本
五、朴素贝叶斯的优缺点
优点:
缺点:
改进方向:
六、朴素贝叶斯的经典应用场景
1. 文本分类
2. 推荐系统
3. 医疗诊断
4. 欺诈检测
七.案例实训
1.鸢尾花分类
2.数字识别
一.什么是朴素贝叶斯
朴素贝叶斯是一种基于贝叶斯定理和特征独立性假设的分类算法。它的核心思想是:通过已知的 “先验概率”,结合数据特征计算 “后验概率”,最终以 “后验概率” 最大的类别作为预测结果。
1.1 从 “概率” 到 “分类”
生活中充满了概率决策的场景:比如看到乌云密布(特征),我们会判断 “下雨(类别)的概率更高”;收到一封含 “优惠”“点击链接” 的邮件(特征),我们会推测 “这是垃圾邮件(类别)的概率更高”。朴素贝叶斯做的正是类似的事 —— 通过特征推断类别,本质是概率驱动的分类。
它的 “朴素” 体现在对特征的假设上:假设所有特征之间相互独立。这个假设虽然简化了计算,但在实际场景中(比如文本分类)往往能得到不错的结果,这也是它 “朴素却实用” 的原因。
二.朴素贝叶斯的数学基础:贝叶斯定理
2.1 贝叶斯定理公式
贝叶斯定理的数学表达式如下: P(A|B) = P(B|A)P(A)/P(B)
其中:
- P(A|B):后验概率,指在已知 “事件 B 发生” 的条件下,“事件 A 发生” 的概率(这是我们最终要计算的目标);
- P(B|A):似然概率,指在 “事件 A 发生” 的条件下,“事件 B 发生” 的概率;
- P(A):先验概率,指 “事件 A 发生” 的概率(在没有任何证据时,对 A 的初始信念);
- P(B):边缘概率,指 “事件 B 发生” 的概率(作为归一化常数,不影响类别判断的相对大小)。
2.2 从贝叶斯定理到朴素贝叶斯分类
在分类问题中,我们需要用特征推测类别。假设输入特征为X=(x_1, x_2, ..., x_n)(比如邮件中的关键词),类别为C(比如 “垃圾邮件” 或 “正常邮件”),则朴素贝叶斯的核心公式可改写为:
P(C∣X)=P(X∣C)/P(C)/p(X)
其中:
- P(C|X):后验概率,即 “已知特征 X 时,属于类别 C 的概率”(我们要最大化的目标);
- P(C):先验概率,即 “类别 C 在所有数据中出现的概率”(比如垃圾邮件占总邮件的比例);
- P(X|C):似然概率,即 “在类别 C 中,特征 X 出现的概率”(比如垃圾邮件中出现 “优惠” 关键词的概率);
- (P(X):边缘概率,对所有类别都相同,计算时可忽略。
2.3 “朴素” 的关键:特征独立性假设
直接计算P(X|C)并不容易,因为特征X可能有多个维度(比如文本有多个关键词)。朴素贝叶斯通过 “特征独立性假设” 简化计算:假设特征(x_1, x_2, ..., x_n)相互独立,则:
P(X|C) = P(x_1|C)P(x_2|C)...P(x_n|C)
即 “联合概率等于边缘概率的乘积”。这个假设大幅降低了计算复杂度,让朴素贝叶斯能高效处理高维数据(比如文本的词向量)。
三、朴素贝叶斯的三种常见类型
根据特征数据的类型不同,朴素贝叶斯衍生出了三种常用模型,分别适用于不同场景:
3.1 高斯朴素贝叶斯(Gaussian Naive Bayes)
适用场景:特征是连续型数据(如身高、体重、鸢尾花的花瓣长度)。 核心思想:假设在每个类别下,特征服从高斯分布(正态分布)。即对于类别C和特征(x_i),P(x_i|C)服从高斯分布(N(\mu_{C,i}, \sigma^2_{C,i})\),其中\(\mu\)是均值,\(\sigma^2\)是方差。
计算时,先通过训练数据计算每个类别下各特征的均值和方差,再用高斯概率密度函数计算\(P(x_i|C)\)。
3.2 多项式朴素贝叶斯(Multinomial Naive Bayes)
适用场景:特征是离散计数数据(如文本中词的出现次数、商品的点击次数)。 核心思想:假设特征的分布服从多项式分布。例如在文本分类中,特征是 “词频”,则\(P(x_i|C)\)表示 “在类别C的文档中,第i个词出现的概率”。
为了避免 “零概率问题”(某个词在类别C中从未出现过,导致\(P(x_i|C)=0\),乘积结果为 0),通常会使用拉普拉斯平滑(Laplace Smoothing),公式为: \(P(x_i|C) = \frac{count(x_i, C) + 1}{count(C) + n}\) 其中\(count(x_i, C)\)是特征\(x_i\)在类别C中的计数,\(count(C)\)是类别C的总计数,n是特征总数。
3.3 伯努利朴素贝叶斯(Bernoulli Naive Bayes)
适用场景:特征是二进制数据(0 或 1,如文本中词是否出现、用户是否点击某个按钮)。 核心思想:假设特征服从伯努利分布(即只有 “出现” 或 “不出现” 两种状态)。例如在文本分类中,特征是 “词是否存在”(1 表示存在,0 表示不存在),则\(P(x_i|C)\)是 “类别C中词i出现的概率”。
它同样会使用拉普拉斯平滑处理零概率问题,且更关注 “特征是否出现” 而非 “出现次数”,适合短文本场景。
四、朴素贝叶斯的工作流程
朴素贝叶斯的训练和预测流程非常简洁,核心是 “统计概率” 和 “计算后验”,具体步骤如下:
步骤 1:数据准备与预处理
- 收集带标签的训练数据(特征X + 类别C);
- 对特征进行预处理:连续特征归一化(高斯朴素贝叶斯)、离散特征编码(多项式 / 伯努利)。
步骤 2:计算先验概率P(C)
- 统计每个类别在训练集中的占比:P(C) = 类别C的样本数 / 总样本数。
步骤 3:计算似然概率P(x_i|C)
- 根据特征类型选择模型(高斯 / 多项式 / 伯努利),统计每个类别下各特征的概率分布:
- 高斯模型:计算每个类别下特征的均值和方差;
- 多项式 / 伯努利模型:统计特征在类别中的计数,并用平滑处理零概率。
步骤 4:预测新样本
- 对新样本的特征X=(x_1, x_2, ..., x_n),计算每个类别的后验概率P(C|X)
- 选择后验概率最大的类别作为预测结果。
五、朴素贝叶斯的优缺点
优点:
- 计算高效:训练时只需统计概率,预测时是简单的乘法运算,时间复杂度低,适合大规模数据;
- 适合高维数据:对文本等稀疏高维特征友好,无需降维也能表现良好;
- 数据需求少:少量样本即可训练(尤其先验概率已知时);
- 可解释性强:结果可通过概率解释,比如 “该邮件是垃圾邮件的概率为 92%”。
缺点:
- 特征独立性假设局限:实际中特征往往不独立(比如 “暴雨” 和 “洪水” 相关),可能影响精度;
- 对特征分布敏感:若实际分布与假设分布(如高斯分布)偏差大,效果会下降;
- 难以学习特征间的交互关系:无法捕捉 “特征 A 且特征 B” 的联合影响。
改进方向:
- 半朴素贝叶斯:放松独立性假设,允许部分特征相关(如通过 “特征选择” 保留重要关联);
- 核函数扩展:对非独立特征用核函数映射到高维空间,间接捕捉关联。
六、朴素贝叶斯的经典应用场景
朴素贝叶斯凭借高效和实用性,在多个领域大放异彩:
1. 文本分类
- 场景:垃圾邮件过滤、新闻主题分类(科技 / 娱乐)、情感分析(正面 / 负面评价);
- 原理:将文本拆分为词袋特征,用多项式 / 伯努利朴素贝叶斯计算 “词特征属于某类别的概率”。
2. 推荐系统
- 场景:基于用户历史行为推荐商品 / 电影;
- 原理:用用户特征(年龄、性别)和物品特征(类型、价格)预测 “用户喜欢该物品的概率”。
3. 医疗诊断
- 场景:根据症状(特征)判断患病类型(类别);
- 原理:结合医学先验知识(疾病发病率\(P(C)\))和症状概率\(P(症状|疾病)\)做推断。
4. 欺诈检测
- 场景:信用卡盗刷、交易欺诈识别;
- 原理:通过交易金额、地点、时间等特征,计算 “该交易为欺诈的概率”。
七.案例实训
1.鸢尾花分类
数据内容如下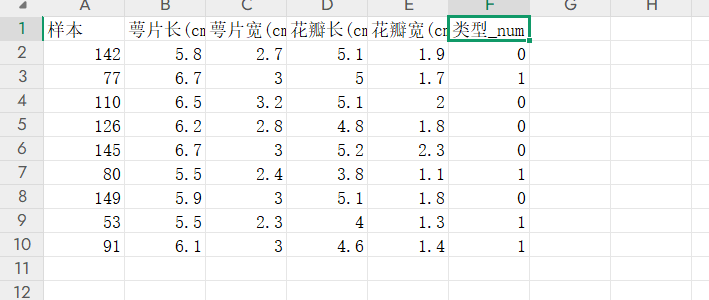
完整代码如下:
需要注意我们可以将训练内容无关的第一列内容样本号删除
# 鸢尾花分类
from sklearn import metrics
from sklearn.naive_bayes import MultinomialNB
import pandas as pd
data = pd.read_excel('鸢尾花测试数据.xlsx')
data=data.drop('样本',axis=1)
X=data.iloc[:,:-1]
y=data.iloc[:,-1]ml=MultinomialNB()
ml.fit(X,y)
predicted=ml.predict(X)
print(ml.score(X,y))
print(metrics.classification_report(y,predicted))2.数字识别
我们可以使用sklearn中自带的数据集,这里我们用自带的数据集load_digits完成手写数字识别
完整代码如下
# 手写数字识别分类
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
digits=load_digits()
X=digits.data
y=digits.target
train_x,test_x,train_y,test_y=train_test_split(X,y,test_size=0.3,random_state=0)
ml.fit(train_x,train_y)
print('===============自测报告==============')
self_predicted=ml.predict(train_x)
print(metrics.classification_report(train_y,self_predicted))
print('===============测试报告==============')
test_predicted=ml.predict(test_x)
print(metrics.classification_report(test_y,test_predicted))===============自测报告==============precision recall f1-score support0 1.00 0.98 0.99 1331 0.88 0.76 0.82 1302 0.92 0.90 0.91 1243 0.99 0.88 0.93 1294 0.96 0.96 0.96 1335 0.98 0.87 0.92 1256 0.98 0.97 0.97 1217 0.91 0.98 0.94 1268 0.73 0.88 0.80 1139 0.77 0.87 0.82 123accuracy 0.91 1257macro avg 0.91 0.91 0.91 1257
weighted avg 0.91 0.91 0.91 1257===============测试报告==============precision recall f1-score support0 0.98 0.98 0.98 451 0.88 0.81 0.84 522 0.94 0.87 0.90 533 1.00 0.81 0.90 544 0.96 0.96 0.96 485 0.98 0.82 0.90 576 0.97 1.00 0.98 607 0.88 0.98 0.93 538 0.89 0.90 0.89 619 0.71 0.93 0.80 57accuracy 0.91 540macro avg 0.92 0.91 0.91 540
weighted avg 0.92 0.91 0.91 540
