《动手学深度学习》读书笔记—9.3深度循环神经网络
到目前为止,我们只讨论了具有一个单向隐藏层的循环神经网络。其中,隐变量和观测值与具体的函数形式的交互方式是相当随意的。只要交互类型建模具有足够的灵活性,这就不是一个大问题。然而,对一个单层来说,这可能具有相当的挑战性。之前在线性模型中,我们通过添加更多的层来解决这个问题。而在循环神经网络中,我们首先需要确定如何添加更多的层,以及在哪里添加额外的非线性,因此这个问题有点棘手。
事实上,我们可以将多层循环神经网络堆叠在一起,通过对几个简单层的组合,产生了一个灵活的机制。特别是,数据可能与不同层的堆叠有关。例如,我们可能希望保持有关金融市场状况(熊市或牛市)的宏观数据可用,而微观数据只记录较短期的时间动态。
图9.3.1描述了一个具有LLL个隐藏层的深度循环神经网络,每个隐状态都连续地传递到当前层的下一个时间步和下一层的当前时间步。
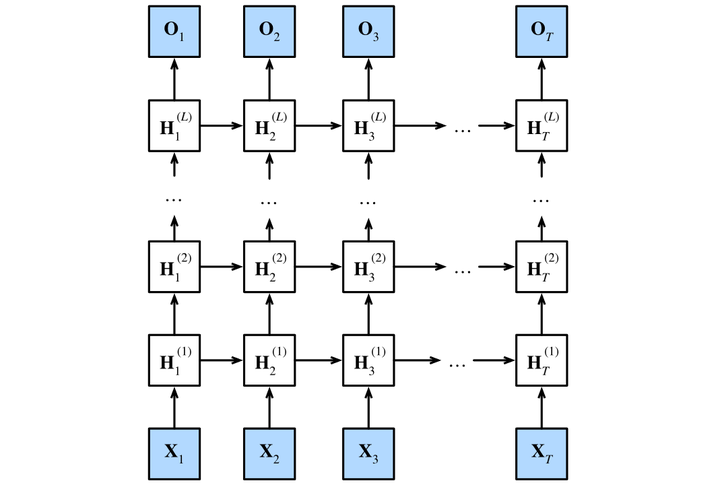
🏷图9.3.1 深度循环神经网络结构
9.3.1 函数依赖关系
我们可以将深度架构中的函数依赖关系形式化,这个架构是由图9.3.1中描述了LLL个隐藏层构成。后续的讨论主要集中在经典的循环神经网络模型上,但是这些讨论也适应于其他序列模型。
假设在时间步ttt有一个小批量的输入数据Xt∈Rn×d\mathbf{X}_t \in \mathbb{R}^{n \times d}Xt∈Rn×d(样本数:nnn,每个样本中的输入数:ddd)。同时,将lthl^\mathrm{th}lth隐藏层(l=1,…,Ll=1,\ldots,Ll=1,…,L)的隐状态设为Ht(l)∈Rn×h\mathbf{H}_t^{(l)} \in \mathbb{R}^{n \times h}Ht(l)∈Rn×h(隐藏单元数:hhh),输出层变量设为Ot∈Rn×q\mathbf{O}_t \in \mathbb{R}^{n \times q}Ot∈Rn×q(输出数:qqq)。设置Ht(0)=Xt\mathbf{H}_t^{(0)} = \mathbf{X}_tHt(0)=Xt,第lll个隐藏层的隐状态使用激活函数ϕl\phi_lϕl,则:
Ht(l)=ϕl(Ht(l−1)Wxh(l)+Ht−1(l)Whh(l)+bh(l))\mathbf{H}_t^{(l)} = \phi_l(\mathbf{H}_t^{(l-1)} \mathbf{W}_{xh}^{(l)} + \mathbf{H}_{t-1}^{(l)} \mathbf{W}_{hh}^{(l)} + \mathbf{b}_h^{(l)})Ht(l)=ϕl(Ht(l−1)Wxh(l)+Ht−1(l)Whh(l)+bh(l))
其中,权重Wxh(l)∈Rh×h\mathbf{W}_{xh}^{(l)} \in \mathbb{R}^{h \times h}Wxh(l)∈Rh×h,Whh(l)∈Rh×h\mathbf{W}_{hh}^{(l)} \in \mathbb{R}^{h \times h}Whh(l)∈Rh×h和偏置bh(l)∈R1×h\mathbf{b}_h^{(l)} \in \mathbb{R}^{1 \times h}bh(l)∈R1×h都是第lll个隐藏层的模型参数。
最后,输出层的计算仅基于第lll个隐藏层最终的隐状态:
Ot=Ht(L)Whq+bq,\mathbf{O}_t = \mathbf{H}_t^{(L)} \mathbf{W}_{hq} + \mathbf{b}_q,Ot=Ht(L)Whq+bq,
其中,权重Whq∈Rh×q\mathbf{W}_{hq} \in \mathbb{R}^{h \times q}Whq∈Rh×q和偏置bq∈R1×q\mathbf{b}_q \in \mathbb{R}^{1 \times q}bq∈R1×q都是输出层的模型参数。
与多层感知机一样,隐藏层数目LLL和隐藏单元数目hhh都是超参数。也就是说,它们可以由我们调整的。另外,用门控循环单元Ht=Zt⊙Ht−1+(1−Zt)⊙H~t\mathbf{H}_t = \mathbf{Z}_t \odot \mathbf{H}_{t-1} + (1 - \mathbf{Z}_t) \odot \tilde{\mathbf{H}}_tHt=Zt⊙Ht−1+(1−Zt)⊙H~t或长短期记忆网络的隐状态Ht=Ot⊙tanh(Ct)\mathbf{H}_t = \mathbf{O}_t \odot \tanh(\mathbf{C}_t)Ht=Ot⊙tanh(Ct)来代替Ht(l)=ϕl(Ht(l−1)Wxh(l)+Ht−1(l)Whh(l)+bh(l))\mathbf{H}_t^{(l)} = \phi_l(\mathbf{H}_t^{(l-1)} \mathbf{W}_{xh}^{(l)} + \mathbf{H}_{t-1}^{(l)} \mathbf{W}_{hh}^{(l)} + \mathbf{b}_h^{(l)})Ht(l)=ϕl(Ht(l−1)Wxh(l)+Ht−1(l)Whh(l)+bh(l))中的隐状态进行计算,可以很容易地得到深度门控循环神经网络或深度长短期记忆神经网络。
9.3.2 简洁实现
实现多层循环神经网络所需的许多逻辑细节在高级API中都是现成的。简单起见,我们仅示范使用此类内置函数的实现方式。以长短期记忆网络模型为例,该代码与之前在9.2长短期记忆网络LSTM中使用的代码非常相似,实际上唯一的区别是我们指定了层的数量,而不是使用单一层这个默认值。像往常一样,我们从加载数据集开始。
import torch
from torch import nn
from d2l import torch as d2l# 批量大小为32(每个批量使用32个子序列), 时间长度为35(子序列的长度为35)
batch_size, num_steps = 32, 35
# 读取时间机器数据集
train_iter, vocab = d2l.load_data_time_machine(batch_size, num_steps)
选择超参数这类架构决策也跟长短期记忆网络一节中的决策非常相似,唯一的区别是现在通过num_layers的值来设定隐藏层数。
🏷nn.LSTM使用说明
https://pytorch.ac.cn/docs/stable/generated/torch.nn.LSTM.html
# 获得词表大小, 隐藏层维数为256, 隐藏层数量为2
vocab_size, num_hiddens, num_layers = len(vocab), 256, 2
# 输入维数是词表大小
num_inputs = vocab_size
# 尝试使用GPU, 失败了就使用CPU
device = d2l.try_gpu()
# 设置长短期记忆网络lstm层
lstm_layer = nn.LSTM(num_inputs, num_hiddens, num_layers)
# 构建模型, rnn_layer选择lstm_layer, vocab_size赋值为len(vocab)
model = d2l.RNNModel(lstm_layer, len(vocab))
# 尝试将模型转移到GPU, 失败了就使用CPU
model = model.to(device)
补充一下d2l.RNNModel函数(在简洁实现RNN中使用过)
#@save
class RNNModel(nn.Module):"""循环神经网络模型"""def __init__(self, rnn_layer, vocab_size, **kwargs):super(RNNModel, self).__init__(**kwargs)self.rnn = rnn_layerself.vocab_size = vocab_sizeself.num_hiddens = self.rnn.hidden_size# 如果RNN是双向的(之后将介绍),num_directions应该是2,否则应该是1if not self.rnn.bidirectional:self.num_directions = 1# 线性层的输入是隐藏层维数,输出是词表大小self.linear = nn.Linear(self.num_hiddens, self.vocab_size)else:self.num_directions = 2# 线性层的输入是隐藏层维数,输出是词表大小self.linear = nn.Linear(self.num_hiddens * 2, self.vocab_size)def forward(self, inputs, state):# 输入X从批量大小*时间长度变为时间长度*批量大小*词表大小X = F.one_hot(inputs.T.long(), self.vocab_size)# 将独热编码转换为float32类型X = X.to(torch.float32)# 将输入和初始状态放入rnn中得到各个时间步的隐状态Y和最后一个时间步的隐状态state# Y的尺寸:时间长度*批量大小*隐藏层维数, state的尺寸:1*批量大小*隐藏层维数Y, state = self.rnn(X, state)# 全连接层首先将Y的形状改为(时间步数*批量大小,隐藏单元数)# 输出output的形状是(时间步数*批量大小,词表大小)。# output和从零开始实现是一样的,dim1是词表大小,表示输入的每个词元产生的输出属于词表中不同词元的概率(可以看成概率)# 调用predict_ch8获得每个输入产生的最大输出的索引,去词表中查找该索引对应的词元作为输出词元output = self.linear(Y.reshape((-1, Y.shape[-1])))return output, statedef begin_state(self, device, batch_size=1):if not isinstance(self.rnn, nn.LSTM):# nn.GRU以张量作为隐状态return torch.zeros((self.num_directions * self.rnn.num_layers,batch_size, self.num_hiddens),device=device)else:# nn.LSTM以元组作为隐状态return (torch.zeros((self.num_directions * self.rnn.num_layers,batch_size, self.num_hiddens), device=device),torch.zeros((self.num_directions * self.rnn.num_layers,batch_size, self.num_hiddens), device=device))
9.3.3 训练和预测
由于使用了长短期记忆网络模型来实例化两个层,因此训练速度被大大降低了。
# 训练轮次500轮, 学习率2
num_epochs, lr = 500, 2
# 训练
d2l.train_ch8(model, train_iter, vocab, lr*1.0, num_epochs, device)
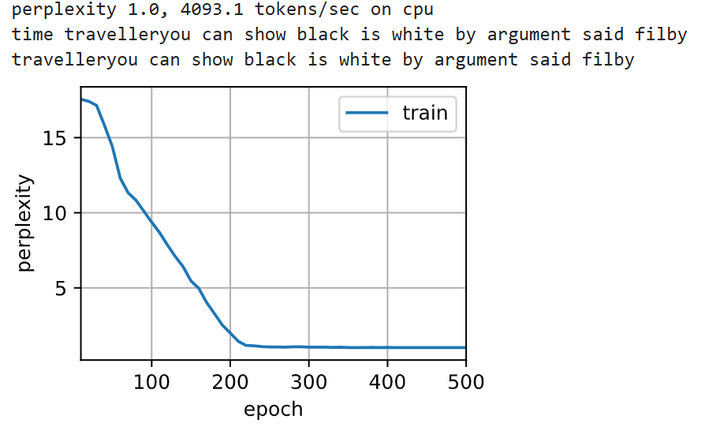
🏷训练结果
9.3.4 小结
- 长短期记忆网络有三种类型的门:输入门、遗忘门和输出门。
- 长短期记忆网络的隐藏层输出包括“隐状态”和“记忆元”。只有隐状态会传递到输出层,而记忆元完全属于内部信息。
- 长短期记忆网络可以缓解梯度消失和梯度爆炸。
