生成式模型 ?判别式模型？用【猫狗分类器】帮助理解！

正确答案与解析：A（贝叶斯模型）​

用「区分猫狗」的案例理解二者的区别！

1. 核心思想对比

• ​生成式模型​：像一个小画家+小侦探
  ➠ 先学会画出所有动物（知道猫/狗长什么样），再根据画的特征判断
  ➠ 典型算法：朴素贝叶斯、GAN、VAE

• ​判别式模型​：像专业质检员
  ➠ 只专注找猫狗之间的差异线​（比如耳朵形状），不关心动物具体长相
  ➠ 典型算法：逻辑回归、SVM、神经网络

---

2. 猫狗分类器

场景：开发一个能区分猫狗图片的AI

• 生成式模型像"画家+侦探"——先学会画出所有数据（P(X,Y)），再根据生成规则判断；
• 判别式模型像"质检员"——直接研究分类标准​（P(Y|X)），不关心数据如何生成。

例如区分猫狗：

• 生成式会建模"猫的像素分布"和"狗的像素分布"（P(X,Y)）；
• 判别式只计算"给定像素时是猫的概率"（P(Y|X)）。

(1) ​生成式模型的工作流​（画家思维）

1. ​学习阶段​：

   • 观察1000张猫图，总结「猫的生成规则」（比如尖耳朵、竖瞳孔）
   • 观察1000张狗图，总结「狗的生成规则」（比如长嘴巴、垂耳朵）
     → 现在能自己画出像猫/狗的图片

2. ​判断阶段​：

   • 拿到新图片时，分别用「猫规则」和「狗规则」生成相似度评分
   • 更像哪个就判为哪类→ "这张图用猫规则生成得分0.8，用狗规则0.3 → 是猫！"

如何工作​：

1. 先分别学习 P(X∥Y=猫) 和 P(X∥Y=狗)（即猫/狗的特征分布）。
2. 再结合先验概率 P(Y)（猫/狗的出现频率），计算联合分布 P(X,Y)=P(X∥Y)P(Y)。
3. 分类时，用贝叶斯定理反推 P(Y∥X)。

​特点​：

• ​能生成数据​：比如画一只新的猫（因为学了 P(X∥Y=猫)）。
• ​需要更多数据​：需准确估计数据分布。
• ​对缺失数据鲁棒​：通过分布插值推断。

​例子​：判断一封邮件是不是垃圾邮件（Spam）：

1. 先学习「垃圾邮件」和「正常邮件」的词频分布 P(单词∥Y)。
2. 新邮件来的时候，比较它更像哪个分布。

---

(2) ​判别式模型的工作流​（质检员思维）

1. ​学习阶段​：

   • 直接对比猫狗图片，找到关键差异​（比如猫耳朵更尖）
   • 建立「猫狗分界线」的数学公式（如：耳朵尖度>0.7是猫）
     → ​不关心猫/狗具体长什么样，只关心区别

2. ​判断阶段​：计算新图片的耳朵尖度=0.8 → 直接输出「猫」→ "不需要知道怎么画猫狗，只要会打分就行"

​如何工作​：直接学习 P(Y∥X)，即「给定输入 X，输出类别 Y 的概率」。

​特点​：

• ​专注分类​：不关心数据怎么生成的，只找分类边界。
• ​计算效率高​：不需要建模复杂的数据分布。
• ​对噪声更鲁棒​：只关注区分特征。

​例子​：逻辑回归判断肿瘤良性/恶性：直接学习「肿瘤大小→恶性概率」的映射，不关心良性/恶性肿瘤的大小分布。

---

3. 关键差异脑图

维度	生成式模型	判别式模型
​目标​	学习数据生成机制​	学习决策边界​
​输出​	能生成新样本	只能分类/回归
​计算复杂度​	通常更高（需建模全数据分布）	通常更低（只关心边界）
​数据要求​	需要充足数据学习分布	对数据量需求相对较小
​典型应用​	图像生成、补全、异常检测	图像分类、垃圾邮件过滤
​数学本质​	建模P(X,Y)的联合分布	建模条件概率 P(Y|X)
典型方法​	朴素贝叶斯、GMM、VAE	逻辑回归、SVM、神经网络

类比场景

​场景​	​生成式模型​	​判别式模型​
​学区分猫狗​	先学会画猫和狗，再比较新图片像谁	直接记住「尖耳朵是猫，圆耳朵是狗」
​学语言翻译​	先学英语和法语的语法，再翻译	直接背「hello→bonjour」的对应关系
​天气预报​	学晴天/雨天的气压、温度分布，再预测	直接学「气压<1000hPa→下雨」的规则

---

4. 检验你是否理解了？

试着回答这些问题（答案在最后）：

1. 为什么生成式模型在数据缺失时表现更好？
2. 判别式模型看到训练集外的数据时会怎样？
3. 用天气预报举例说明两者的区别？

暂停，思考ing。。。。。

---

答案
生成式模型通过分布估计可以插值，判别式模型对未知数据容易失效
可能因未学习过该特征而误判（如遇到无耳猫就崩溃）
生成式=学习晴/雨天的所有气象数据规律；判别式=只关注温度/湿度如何影响下雨概率

• 生成式​：学「数据生成规则」→ 能造数据，但分类可能不够精准。
• ​判别式​：学「分类边界」→ 专注分类，效率高，但不能生成数据。

• 需要生成或解释数据？→ 生成式
• 只要分类精度？→ 判别式

5. ​关于 P(X,Y) 的详细解释​

---

​1. 数学定义​

​​P(X,Y) 是联合概率分布，表示：

• ​​X​​：输入特征（如身高=180cm）
• ​​Y​​：输出类别（如性别=男/女）
• ​​P(X,Y)​​：特征 X 和类别 Y ​同时出现的概率。

---

​2. 在生成式模型中的具体含义​

以「身高判断性别」为例，生成式模型通过以下两步建模 P(X,Y)：

1. ​学习条件概率​：
   • P(身高=180∥男)=0.1（男性中身高180cm的概率）
   • P(身高=180∥女)=0.01
2. ​结合先验概率​：
   • P(男) 和 P(女)（性别本身的分布，如男女比例）
3. ​计算联合分布​：
   • P(身高=180,男)=P(身高=180∥男)⋅P(男)
   • P(身高=180,女)=P(身高=180∥女)⋅P(女)

​最终目标​：通过 P(X,Y) 反推 P(Y∥X)（贝叶斯定理）。

---

​3. 为什么判别式模型不关心 P(X,Y)？​​

​判别式模型直接学习 P(Y∥X)，例如：

• 逻辑回归输出 P(男∥身高=180)=
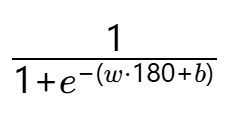
• ​无需计算​ P(身高=180∥男) 或 P(男)，跳过了联合分布建模。​

---

4. 举例说明​

假设数据集中：

• 男性占比 P(男)=0.6，女性 P(女)=0.4
• 男性中身高180cm的概率 P(180∥男)=0.1
• 女性中身高180cm的概率 P(180∥女)=0.01

则联合概率：

• P(180,男)=0.1×0.6=0.06
• P(180,女)=0.01×0.4=0.004

​生成式模型会利用这两个值计算

​​P(X,Y) 是数据和类别的联合概率，生成式模型靠它「造数据」，判别式模型绕过它「划边界」。

---

6. ​关于 P(Y∣X) 的详细释​

---

​1. 数学定义​

​​P(Y∣X) 是条件概率，表示：

• ​在已知输入特征 X 的前提下，类别 Y 发生的概率。
• ​公式​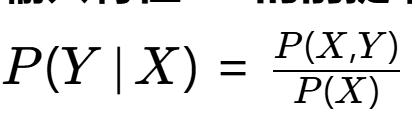：（贝叶斯定理展开）
  • 其中 P(X) 是特征 X 的边际概率（所有类别下 X 出现的总概率）。

---

​2. 在判别式模型中的具体含义​

以「身高判断性别」为例：

• ​判别式模型直接建模 P(男∣身高=180)​，无需关心：
  • 男性/女性的身高分布 P(身高∣Y)
  • 性别本身的先验概率 P(Y)
• ​直接通过数据学习映射规则，例如：
  • 逻辑回归：P(男∣身高)=
  • 神经网络：最后一层Softmax输出 P(Y∣X)。

---

​7. ​关键区别​

• 生成式模型通过 P(X,Y) ​间接计算 P(Y∣X)（贝叶斯推断）；
• 判别式模型 ​直接拟合 P(Y∣X)（函数逼近）。

​生成式模型​	​判别式模型​
先建模 P(X,Y)=P(X∥Y)P(Y)	直接建模 P(X∥Y)
需要学习数据生成机制	仅学习分类边界
计算复杂（需估计分布参数）	计算高效（仅优化分类目标）

---

8. 为什么判别式模型更常用？​​

1. ​效率高​：省去分布估计步骤，直接优化分类性能。
2. ​对噪声鲁棒​：不依赖数据分布假设（如高斯分布）。
3. ​适合高维数据​：图像、文本等复杂特征难以建模 P(X∣Y)。

​例外​：当需要生成数据或处理缺失值时，生成式模型更优（如GAN、VAE）。

---

9. 实例对比​

​任务​：判断肿瘤良性（Y=0）或恶性（Y=1）

• ​生成式模型（朴素贝叶斯）​​：

  1. 分别学习良性/恶性肿瘤的特征分布 P(肿瘤大小∥Y=0) 和 P(肿瘤大小∥Y=1)。
  2. 计算联合概率 P(肿瘤大小,Y)=P(肿瘤大小∥Y)P(Y)。
  3. 反推 P(Y∥肿瘤大小)。

• ​判别式模型（逻辑回归）​​：直接拟合 P(Y=1∥肿瘤大小)=。

---

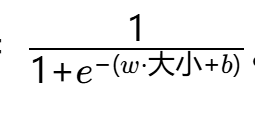10. 常见误区​

• ​误区1​：认为 P(Y∣X) 必须通过贝叶斯定理计算。
  • ​纠正​：判别式模型直接参数化 P(Y∣X)（如神经网络）。
• ​误区2​：认为生成式模型一定更强大。
  • ​纠正​：判别式模型在分类任务上通常表现更好（Vapnik原则）。

11.案例：肿瘤预测

1. 分别学习良性/恶性肿瘤的特征分布 P(肿瘤大小∥Y=0) 和 P(肿瘤大小∥Y=1)。
2. 计算联合概率 P(肿瘤大小,Y)=P(肿瘤大小∥Y)P(Y)。
3. 反推 P(Y∥肿瘤大小)。

疑问：具体咋做呢？

我们通过一个具体的医学诊断案例，完整演示生成式模型（朴素贝叶斯）如何计算 P(Y∣X)。假设数据如下：

---

​案例背景​

​任务​：根据肿瘤大小（单位：cm）判断良性（Y=0）或恶性（Y=1）
​数据集统计​：

• 共100例患者，其中60例良性（Y=0），40例恶性（Y=1）
• 良性肿瘤大小服从 N(μ=2,σ=1)
• 恶性肿瘤大小服从 N(μ=5,σ=1.5)

​待预测样本​：肿瘤大小 X=4cm

---

​生成式模型计算步骤​

​第1步：学习先验概率 P(Y)​​

• P(Y=0)=0.6
• P(Y=1)=0.4

​第2步：学习条件概率 P(X∣Y)​​

假设肿瘤大小服从高斯分布，计算概率密度：

• ​良性分布 P(X∣Y=0)​​：N(μ=2,σ=1)

  

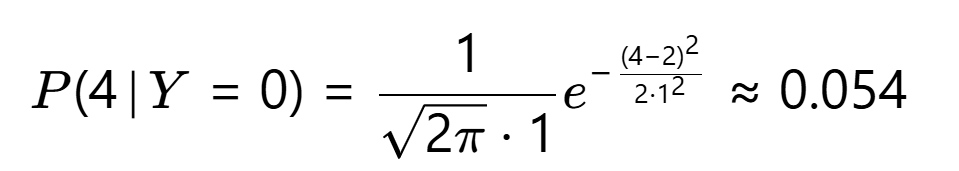
• ​恶性分布 P(X∣Y=1)​​：N(μ=5,σ=1.5)

  

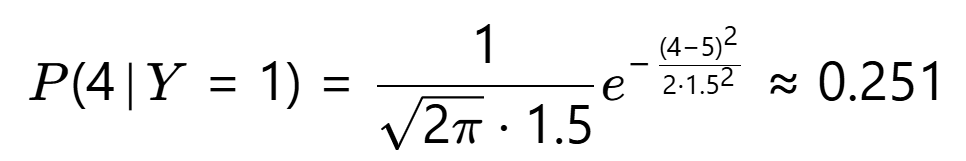
​第3步：计算联合概率 P(X,Y)​​

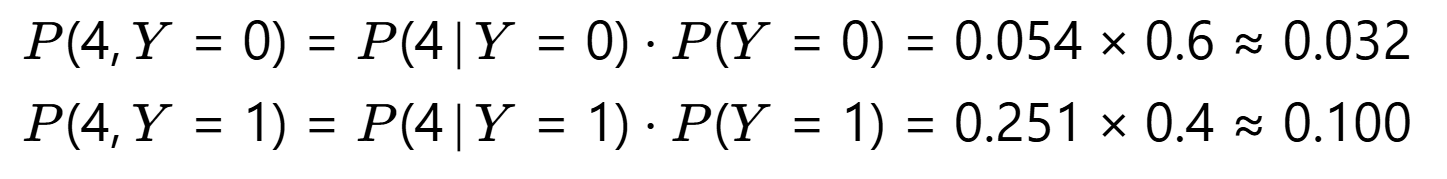
​第4步：计算边际概率 P(X=4)​​

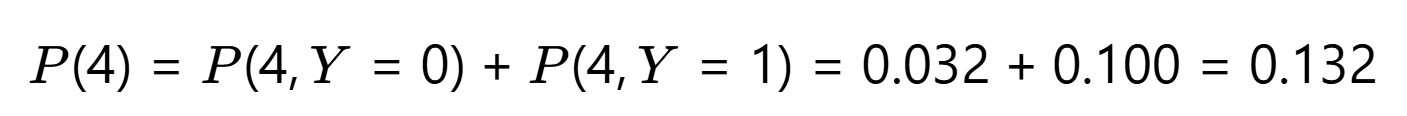
​第5步：反推 P(Y∣X=4)​​

---

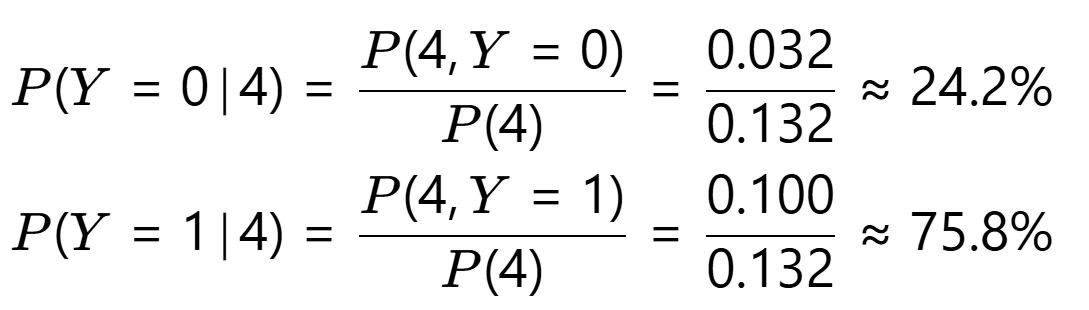
​诊断结论​

• ​恶性概率75.8%​，良性概率24.2% → 判定为恶性（若阈值设为50%）。

---

​对比判别式模型（逻辑回归）​​

假设已训练好逻辑回归模型：

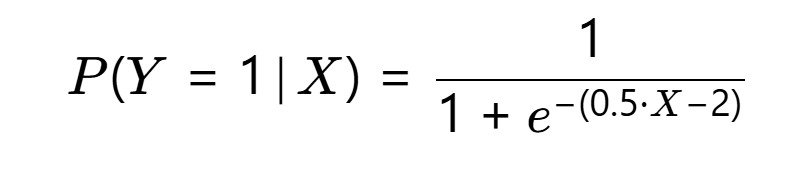
对 X=4(直接输出，无需分布假设)：

---

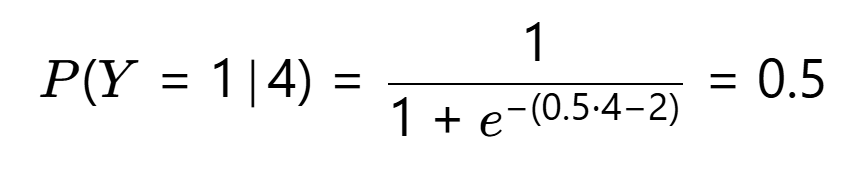
​关键对比​

​步骤​	​生成式模型​	​判别式模型​
1. 需要学习分布	需假设 P(X∥Y) 的分布形式（如高斯）	无需任何分布假设
2. 计算复杂度	高（需估计分布参数）	低（直接拟合参数）
3. 结果解释性	可解释性强（明确概率来源）	黑箱（仅知分类结果）
4. 对数据量的需求	需足够数据估计分布	相对较少

---

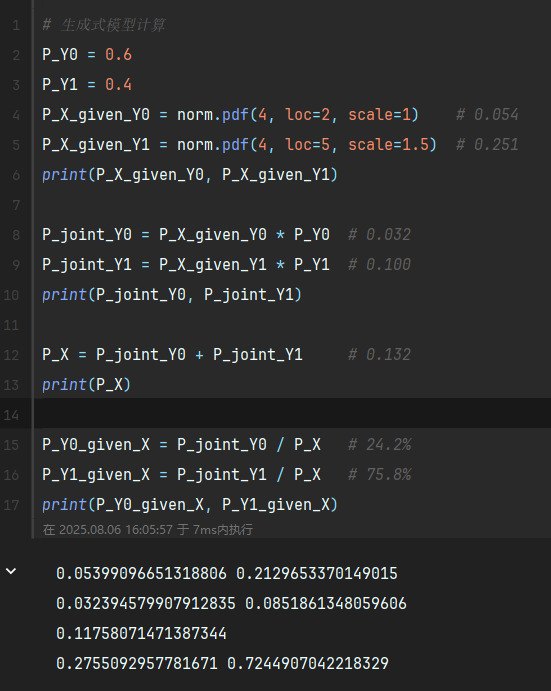
​附：Python代码验证​

from scipy.stats import norm# 生成式模型计算
P_Y0 = 0.6
P_Y1 = 0.4
P_X_given_Y0 = norm.pdf(4, loc=2, scale=1)    # 0.054
P_X_given_Y1 = norm.pdf(4, loc=5, scale=1.5)  # 0.251P_joint_Y0 = P_X_given_Y0 * P_Y0  # 0.032
P_joint_Y1 = P_X_given_Y1 * P_Y1  # 0.100P_X = P_joint_Y0 + P_joint_Y1     # 0.132
P_Y0_given_X = P_joint_Y0 / P_X   # 24.2%
P_Y1_given_X = P_joint_Y1 / P_X   # 75.8%