排序算法(二)
一.快速排序
1)基本原理:
选择一个「基准元素」,将数组分为两部分:左半部分元素均小于基准,右半部分均大于基准;然后递归对左右两部分重复此操作,直至子数组长度为 1(天然有序)


//Hoare实现public void quickSor(int[] array) {quick(array,0,array.length-1);}public void quick(int[] array,int left,int right) {if (left >= right) {return;}// 这是对快排进行的优化if (right - left <= 10) {// 10只是示范,该数值可以改变,选取合适,插入排序可以有效优化时空复杂度insertSortRange(array,left,right);return;}// 三数取中法优化时空复杂度int index = midOfThree(array,left,right);swap(array,index, left);int pivot = partition(array,left,right);quick(array,left,pivot-1);quick(array,pivot+1,right);}private static void insertSortRange(int[] array,int begin,int end) {for (int i = begin+1; i <= end; i++) {int tmp = array[i];int j = i-1;for (; j >= begin ; j--) {if(array[j] > tmp) {array[j+1] = array[j];}else {break;}}array[j+1] = tmp;}}// 得到中间值的下标public int midOfThree(int[] array,int start,int end) {int mid = (start + end)/2;if (array[start] > array[end]) {if(array[mid] > array[start]) {return start;}else if(array[mid] > array[end]) {return mid;}else {return end;}} else {if(array[mid] > array[start]) {return start;}else if(array[mid] < array[end]) {return end;}else {return mid;}}}// 寻找基准public int partition(int[] array,int left,int right) {int i = left;while (left < right) {while (left < right && array[right] >= array[i]) {right--;}while (left < right && array[left] <= i) {left++;}swap(array,left,right);}swap(array,left,i);return left;}public void swap(int[] array,int a,int b) {int tmp = array[a];array[a] = array[b];array[b] = tmp;}
2)核心点
- 快速排序可能出现栈溢出问题,因此应考虑优化
如例子中的三数取中,结合插入排序都可以降低递归次数,改善在极端情况下的时空复杂度,
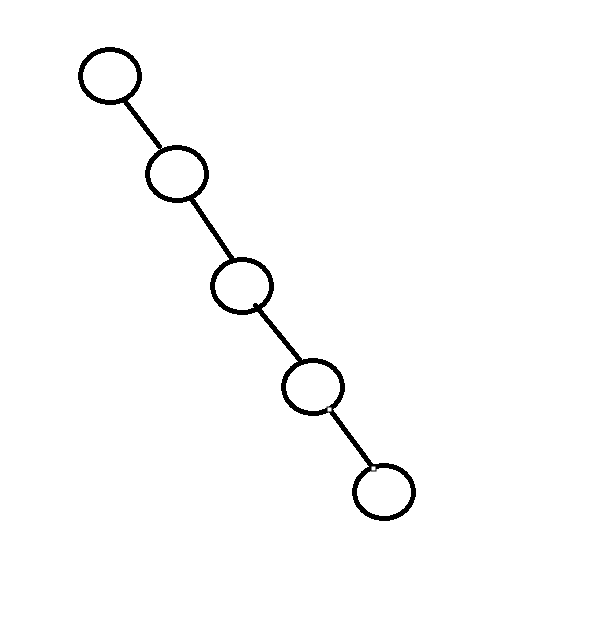
层层递归的过程类似于二叉树,

如图:无左边分支,树的高度较高,空间复杂度变高
而经过优化后:树更加平衡,坐树执行完后释放资源再执行右树,因此被浪费的不可释放资源降低

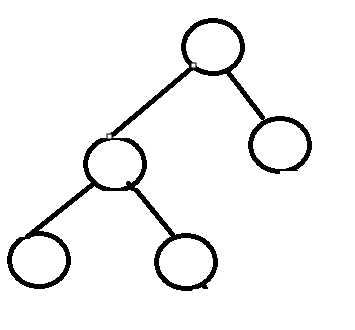
- 而结合插入排序同样是优化了树的高度
- 快速排序是不稳定的
- Hoare方法注意partition中内层双循环的循环条件与执行顺序
3)快速排序另外版本的实现
上述例子为Hoare实现
还有两种快速排序的实现方式,差距在于partition方法,
1.挖坑法

public int partition2(int[] array,int left,int right) {int i = left;int tmp = array[left];while (left < right) {while (left < right && array[right] >= array[i]) {right--;}array[i] = array[right];while (left < right && array[left] <= i) {left++;}array[right] = tmp;i++;}swap(array,left,i);return left;}
2.前后指针法

public int partition3(int[] array,int left,int right) {int i = left;int j = i+1;while (j < right) {if (array[j] < array[left] && array[++i] != array[j]) {swap(array,j,i);}j++;}swap(array,i,left);return i;}
4)快速排序的非递归实现(利用栈)
public void quickSortNor(int[] array) {Stack<Integer> stack = new Stack<>();int left = 0;int right = array.length-1;int piovt = partition(array,left,right);if(piovt - 1 > left) {stack.push(left);stack.push(piovt-1);}if(piovt + 1 < right) {stack.push(piovt+1);stack.push(right);}while (!stack.isEmpty()) {right = stack.pop();left = stack.pop();piovt = partition(array,left,right);if(piovt - 1 > left) {stack.push(left);stack.push(piovt-1);}if(piovt + 1 < right) {stack.push(piovt+1);stack.push(right);}}}
二.归并排序
1)基本概念
归并排序(Merge Sort)是分治法(Divide and Conquer) 的经典应用,核心思想是 “先分后合”:将数组不断拆分至最小单位(单个元素),再逐步将有序的子数组合并为更大的有序数组,最终得到完整的有序数组
是稳定的排序


public void mergeSortFunc(int[] array,int left,int right){if(left >= right) return;int mid = (left+right)/2;mergeSortFunc(array,left,mid);mergeSortFunc(array,mid +1 ,right);merge(array,left,right,mid);}public void merge(int[] array, int left, int right, int mid) {int s1 = left;int s2 = mid + 1;int[] tmpArr = new int[right - left + 1];int k = 0;// !!!!注意循环结束条件while (s1 <= mid && s2 <= right) {if (array[s1] >= array[s2]) {tmpArr[k++] = array[s2++];} else {tmpArr[k++] = array[s1++];}}// !!!!处理左右两数组不等长情况while (s1 <= mid) {tmpArr[k++] = array[s1++];}while (s2 <= right) {tmpArr[k++] = array[s2++];}// !!!!此处易错for (int i = 0; i < tmpArr.length; i++) {array[i+left] = tmpArr[i];}}public void mergeSort(int[] array) {mergeSortFunc(array,0,array.length-1);}// 非递归实现并和排序public void mergeSortNor(int[] array) {int gap = 1;while (gap < array.length) {for (int i = 0; i < array.length; i += 2*gap) {int left = i;int mid =left+gap-1;int right = mid+gap;if(mid >= array.length) {mid = array.length-1;}if(right >= array.length) {right = array.length-1;}merge(array,left,right,mid);}gap *= 2;}}
2)归并排序在外部排序的运用
外部排序是处理大规模数据(无法一次性加载到内存)的经典方法,而归并排序因其分治特性成为外部排序的核心实现方式
示例场景:
假设需排序一个 10GB 的文本文件(每行一个整数),但内存仅能处理 1GB 数据。通过外部排序的分治思想,可将其拆分为 10 个 1GB 的块,分别排序后合并
- 拆分文件:
将 10GB 文件按 1GB 为单位拆分为 10 个块
每个块独立读入内存,使用快速排序或堆排序完成内部排序,生成有序的顺串。
最终得到 10 个有序的顺串文件 - 归并(以二路归并为例):
将两个分割后的文件的部分放入内存比较,再对磁盘进行操作(如上方merge的双数组方法,把A的一部分和B的一部分分别读入内存,排序后写入磁盘)
三.计数排序
计数排序是一种非比较型排序算法,其核心思想是通过统计待排序元素中每个值出现的次数,再根据次数确定元素在结果数组中的位置。它适用于整数排序(或可映射为整数的场景),且在取值范围较小时效率极高

public void countSort(int[] array) {int minVal = array[0];int maxVal = array[0];//1、求当前数组的最大值 和 最小值for (int i = 1; i < array.length; i++) {if(array[i] < minVal) {minVal = array[i];}if(array[i] > maxVal) {maxVal = array[i];}}//2.跟进最大值 和 最小值 来确定数组的大小int[] count = new int[maxVal-minVal+1];//3、遍历原来的数组 开始计数for (int i = 0; i < array.length; i++) {count[array[i]-minVal]++;}//4、遍历计数cout 把 当前元素 写回 arrayint index = 0;//重新表示array数组的下标for (int i = 0; i < count.length; i++) {while (count[i] > 0) {array[index] = i+minVal;index++;count[i]--;}}}
