当前位置：首页 > news >正文

Transformer核心机制：QKV全面解析

news 2025/8/5 14:26:44

引言

如果说Transformer是一座宏伟的建筑，那么QKV机制就是支撑这座建筑的核心支柱。理解QKV机制，不仅能帮助我们深入掌握Transformer的工作原理，更能为我们在实际应用中优化模型性能提供重要指导。本文将从最基础的概念出发，通过生动的类比、详细的数学推导、直观的图表展示和完整的代码实现，带你彻底理解QKV机制的精妙之处。
单头注意力机制与多头注意力机制

Self-Attention 结构（左），多头注意力机构（右）

一、基础概念：什么是注意力机制？

1.1 从人脑注意力说起

要理解QKV机制，我们首先需要理解什么是注意力。想象一下，当你在一个嘈杂的咖啡厅里与朋友聊天时，尽管周围有各种声音——咖啡机的嗡嗡声、其他客人的谈话声、背景音乐等，但你的大脑能够自动"过滤"掉这些干扰，专注于朋友的声音。这就是注意力机制的本质：有选择地关注重要信息，忽略无关信息。

从数学角度来看，注意力机制本质上就是一个加权过程。对于重要的信息，我们给予较高的权重（接近1）；对于不重要的信息，我们给予较低的权重（接近0）。这样，通过加权求和，我们就能得到一个融合了重要信息的表示。

1.2 计算机中的注意力机制

在深度学习领域，注意力机制的发展经历了几个重要阶段。最初，研究者们在序列到序列（seq2seq）模型中引入了注意力机制，用于解决长序列信息丢失的问题。

传统的seq2seq模型存在一个明显的瓶颈：编码器需要将整个输入序列压缩成一个固定长度的向量，然后解码器基于这个向量生成输出序列。这种设计在处理长序列时容易丢失信息，特别是序列开头的信息。

注意力机制的引入解决了这个问题。在每个解码步骤中，模型不再只依赖于固定的编码向量，而是能够"回头看"整个输入序列，并根据当前的解码状态决定应该关注输入序列的哪些部分。

1.3 自注意力的革命性突破

虽然传统的注意力机制已经很有效，但它仍然需要编码器-解码器的架构。Transformer的革命性贡献在于提出了**自注意力（Self-Attention）**机制。

自注意力的核心思想是：让序列中的每个元素都能直接与序列中的所有其他元素建立连接，包括它自己。这样，模型就能够捕捉到序列内部的复杂依赖关系，而不需要通过递归或卷积的方式逐步传递信息。

举个例子，考虑句子"The animal didn’t cross the street because it was too tired"。在这个句子中，代词"it"指代的是"animal"而不是"street"。自注意力机制能够让模型在处理"it"时，自动关注到"animal"，从而正确理解句子的含义。

二、QKV机制核心解析

2.1 QKV的定义和含义

QKV机制是自注意力的核心实现方式，其中Q、K、V分别代表：

Q (Query, 查询)：表示"我想要什么信息"
K (Key, 键)：表示"我能提供什么信息"
V (Value, 值)：表示"我实际包含的信息"

这个设计灵感来源于数据库的检索系统。想象你在一个图书馆里查找资料：

Query（查询）：你想要查找的主题，比如"机器学习"
Key（键）：每本书的索引信息，比如书名、关键词、摘要等
Value（值）：书籍的实际内容

当你提出查询时，图书馆系统会将你的查询与所有书籍的索引信息进行匹配，找出最相关的书籍，然后返回这些书籍的内容。QKV机制的工作原理与此完全类似。

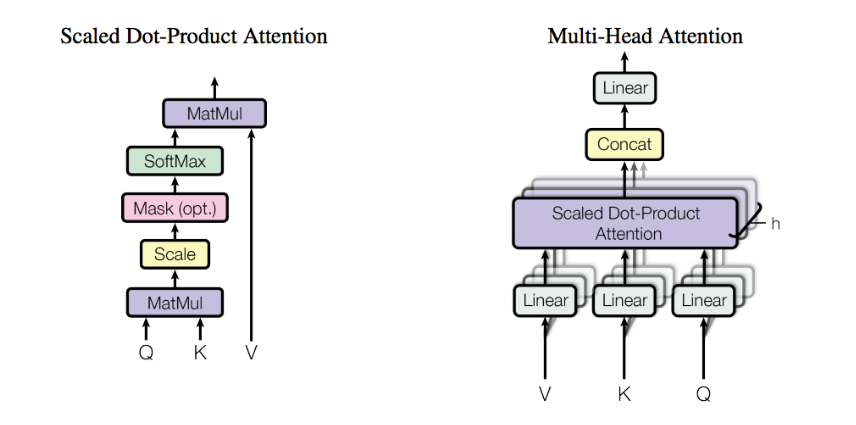
2.2 流程图解QKV

在这里插入图片描述

在Transformer中，Q、K、V都是通过对输入进行线性变换得到的。假设我们有输入矩阵 $\in \mathbb{R}^{n \times d}$ ，其中 $n$ 是序列长度， $d$ 是特征维度。

输入序列 X (batch_size, seq_len, d_model)│├─────────────────┬─────────────────┬─────────────────│                 │                 │▼                 ▼                 ▼
┌─────────┐      ┌─────────┐      ┌─────────┐
│ X × W_Q │      │ X × W_K │      │ X × W_V │
└─────────┘      └─────────┘      └─────────┘│                 │                 │▼                 ▼                 ▼
┌─────────┐      ┌─────────┐      ┌─────────┐
│    Q    │      │    K    │      │    V    │
│ (查询)   │      │ (键值)   │      │ (数值)   │
└─────────┘      └─────────┘      └─────────┘

数学表达式为：

$Q = XW_Q\\ K = XW_K\\ V = XW_V\\$

其中：

$WQ∈Rd×dqW_Q \in \mathbb{R}^{d \times d_q}$ 是查询权重矩阵
$WK∈Rd×dkW_K \in \mathbb{R}^{d \times d_k}$ 是键权重矩阵
$WV∈Rd×dvW_V \in \mathbb{R}^{d \times d_v}$ 是值权重矩阵

这三个权重矩阵是模型的可学习参数，在训练过程中会不断优化，以学习如何最好地提取查询、键和值的表示。

2.3 注意力计算的完整流程

有了Q、K、V之后，注意力的计算分为四个步骤：

步骤1: 计算相似度矩阵
┌─────┐    ┌─────┐    ┌─────────────┐
│  Q  │ ×  │ K^T │ =  │ Similarity  │
│     │    │     │    │   Matrix    │
└─────┘    └─────┘    └─────────────┘│▼
步骤2: 缩放操作
┌─────────────┐    ┌─────┐    ┌─────────────┐
│ Similarity  │ ÷  │√d_k │ =  │   Scaled    │
│   Matrix    │    │     │    │  Attention  │
└─────────────┘    └─────┘    └─────────────┘│▼
步骤3: Softmax归一化
┌─────────────┐              ┌─────────────┐
│   Scaled    │  Softmax()   │ Attention   │
│  Attention  │ ──────────►  │  Weights    │
└─────────────┘              └─────────────┘│▼
步骤4: 加权求和
┌─────────────┐    ┌─────┐    ┌─────────────┐
│ Attention   │ ×  │  V  │ =  │   Output    │
│  Weights    │    │     │    │             │
└─────────────┘    └─────┘    └─────────────┘

步骤1：计算相似度矩阵

首先计算查询Q和键K之间的相似度。这里使用点积来衡量相似度：

$Similarity=QKT\text{Similarity} = QK^T$

得到的相似度矩阵的维度是 $\times n)$ ，其中 $Similarityi,j\text{Similarity}_{i,j}$ 表示第 $i$ 个查询与第 $j$ 个键之间的相似度。

步骤2：缩放操作

为了防止点积结果过大导致梯度消失，我们将相似度矩阵除以 $dk\sqrt{d_k}$ ：

$Scaled=QKTdk\text{Scaled} = \frac{QK^T}{\sqrt{d_k}}$

这个缩放因子的选择有深刻的数学原理。当 $d_k$ 较大时，点积的方差会变大，这会导致softmax函数的输出过于集中在某些位置，使得梯度变得很小。除以 $dk\sqrt{d_k}$ 可以使方差保持在合理范围内。

步骤3：Softmax归一化

对缩放后的相似度矩阵应用softmax函数，将其转换为概率分布：

$Weights=softmax(QKTdk)\text{Attention Weights} = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)$

softmax函数确保每一行的权重和为1，这样就得到了一个有效的概率分布。

步骤4：加权求和

最后，使用注意力权重对值V进行加权求和：

$Weights×V\text{Output} = \text{Attention Weights} \times V$

完整的注意力公式

将上述四个步骤合并，我们得到了著名的注意力公式：

$Attention(Q,K,V)=softmax(QKTdk)V\text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V$

这个公式虽然看起来简洁，但包含了注意力机制的全部精髓。

三、深入理解：为什么这样设计？

3.1 数学原理深度解析

点积相似度的几何意义

为什么使用点积来计算Q和K之间的相似度？这背后有深刻的几何意义。

两个向量的点积可以表示为： $a⃗⋅b⃗=∣a⃗∣∣b⃗∣cos⁡θ\vec{a} \cdot \vec{b} = |\vec{a}||\vec{b}|\cos\theta$ ，其中 $θ\theta$ 是两个向量之间的夹角。当两个向量方向相同时（ $θ=0\theta = 0$ ），点积最大；当两个向量垂直时（ $θ=90°\theta = 90°$ ），点积为0；当两个向量方向相反时（ $θ=180°\theta = 180°$ ），点积最小。

在高维空间中，如果我们将Q和K都归一化到单位长度，那么它们的点积就直接等于 $cos⁡θ\cos\theta$ ，这是一个很好的相似度度量。相似的向量会有较大的点积值，不相似的向量会有较小的点积值。

缩放因子 $dk\sqrt{d_k}$ 的作用

假设Q和K的每个元素都是独立的随机变量，均值为0，方差为1。那么它们的点积的方差就是 $d_k$ 。当 $d_k$ 很大时，点积的值会变得很大，这会导致softmax函数的输出过于集中。

具体来说，如果softmax的输入值很大，比如 $[100, 1, 1]$ ，那么输出会接近 $[1, 0, 0]$ ，这意味着注意力几乎完全集中在一个位置上，其他位置的梯度会变得很小。除以 $dk\sqrt{d_k}$ 可以将点积的方差控制在1左右，使得softmax的输出更加平滑，梯度更加稳定。

3.2 直观理解和生活化类比

购物搜索的类比

让我们用一个更具体的例子来理解QKV机制。假设你在电商网站上搜索"红色连衣裙"：

数据库查询类比:
┌─────────────┐    ┌─────────────┐    ┌─────────────┐
│    Query    │    │     Key     │    │    Value    │
│   (查询)     │    │   (索引)     │    │   (数据)     │
├─────────────┤    ├─────────────┤    ├─────────────┤
│"红色连衣裙"  │ ←→ │"商品描述"    │ →  │"商品信息"    │
│             │    │"关键词"     │    │"详细内容"    │
└─────────────┘    └─────────────┘    └─────────────┘│                   │                   │└───────────────────┼───────────────────┘│相似度匹配

Query（查询）：你输入的搜索词"红色连衣裙"
Key（键）：每个商品的描述信息，比如"优雅红色长袖连衣裙"、“蓝色牛仔裤”、"红色T恤"等
Value（值）：商品的详细信息，包括价格、图片、评价等

搜索引擎会计算你的查询与每个商品描述的相似度，然后根据相似度对商品进行排序和加权，最终返回最相关的商品信息。

Transformer Self-Attention 具体示例

下面以一个 3 个词（“我”, “爱”, “你”）的序列为例，完整演示 Self-Attention 中 Q、K、V 的计算流程。

假设 3 个 token 的 embedding 为 4 维，映射后 $d_k = d_v = 2$ 。

$\begin{bmatrix} 1 & 0 & 1 & 0 \\ 0 & 2 & 0 & 1 \\ 1 & 1 & 1 & 1 \end{bmatrix},\quad W^Q = W^K = W^V = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0 \\ 0 & 1 \end{bmatrix}$

线性映射 Q, K, V

$=\begin{bmatrix}2 & 0\\0 & 3\\2 & 2\end{bmatrix}$
相似度打分 Score = $QK^T$
$\begin{bmatrix}2&0\\0&3\\2&2\end{bmatrix}\begin{bmatrix}2&0&2\\0&3&2\end{bmatrix} = \begin{bmatrix}4&0&4\\0&9&6\\4&6&8\end{bmatrix}$
缩放 + 归一化 Weights = softmax( $Score2\tfrac{Score}{\sqrt{2}}$ )
行原始分数除以 √2 Softmax 权重
“我” [4, 0, 4] [2.83, 0, 2.83] [0.43, 0.14, 0.43]
“爱” [0, 9, 6] [0, 6.36, 4.24] [0.01, 0.71, 0.28]
“你” [4, 6, 8] [2.83, 4.24, 5.66] [0.05, 0.26, 0.69]
加权求和输出 $\mathrm{Weights}\cdot V$
- $O_1$ (“我”)：
  
  $[0.43,0.14,0.43]\cdot\begin{bmatrix}2&0\\0&3\\2&2\end{bmatrix} = [1.72,\;1.29]$
- $O_2$ (“爱”):
  
  $[0.01,0.71,0.28]\cdot\begin{bmatrix}2&0\\0&3\\2&2\end{bmatrix} = [0.57,\;1.84]$
- $O_3$ (“你”):
  
  $[0.05,0.26,0.69]⋅[200322]=[1.53,;2.07][0.05,0.26,0.69]\cdot\begin{bmatrix}2&0\\0&3\\2&2\end{bmatrix} = [1.53,;2.07]$

行	原始分数	除以 √2	Softmax 权重
“我”	[4, 0, 4]	[2.83, 0, 2.83]	[0.43, 0.14, 0.43]
“爱”	[0, 9, 6]	[0, 6.36, 4.24]	[0.01, 0.71, 0.28]
“你”	[4, 6, 8]	[2.83, 4.24, 5.66]	[0.05, 0.26, 0.69]

4. 最终上下文表示

$\begin{bmatrix} 1.72 & 1.29 \\ 0.57 & 1.84 \\ 1.53 & 2.07 \end{bmatrix}$

每行 $O_i$ 就是第 $i$ 个 token 的上下文向量：
- $O_1$ 融合了“我”和“你”的信息；
- $O_2$ 主要体现“爱”自身并适当借鉴“你”；
- $O_3$ 强调“你”的信息，并参考了“爱”。

这些上下文向量可以送入后续的前馈网络、残差连接和 LayerNorm，用于分类、翻译或文本生成任务。

四、多头注意力机制

4.1 为什么需要多头？

单头注意力虽然已经很强大，但它有一个重要的局限性：只能学习一种类型的关系。在自然语言中，词与词之间可能存在多种不同类型的关系：

语法关系：主语与谓语、修饰语与被修饰语等
语义关系：同义词、反义词、上下位关系等
位置关系：相邻词、远距离依赖等
功能关系：实体与属性、动作与对象等

单头注意力只能学习其中一种关系，而多头注意力允许模型同时学习多种不同的关系模式。

4.2 多头注意力的实现

多头注意力的核心思想是：将输入投影到多个不同的子空间，在每个子空间中独立计算注意力，然后将结果合并。

                    输入 X│┌─────────────┼─────────────┐│             │             │▼             ▼             ▼┌───────┐     ┌───────┐     ┌───────┐│Head 1 │     │Head 2 │ ... │Head h ││       │     │       │     │       ││Q₁K₁V₁ │     │Q₂K₂V₂ │     │QₕKₕVₕ │└───────┘     └───────┘     └───────┘│             │             │└─────────────┼─────────────┘│Concat│▼┌─────────────┐│ Linear(W^O) │└─────────────┘│▼Output

数学表达式：

对于第 $i$ 个头：
$headi=Attention(QWiQ,KWiK,VWiV)\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)$

多头注意力的最终输出：
$MultiHead(Q,K,V)=Concat(head1,head2,...,headh)WO\text{MultiHead}(Q,K,V) = \text{Concat}(\text{head}_1, \text{head}_2, ..., \text{head}_h)W^O$

五、代码实现详解

5.1 PyTorch实现

让我们从头开始实现一个完整的多头自注意力模块：

import torch
import torch.nn as nn
import torch.nn.functional as F
import mathclass MultiHeadAttention(nn.Module):"""多头自注意力机制的完整实现"""def __init__(self, d_model, num_heads, dropout=0.1):super(MultiHeadAttention, self).__init__()# 确保d_model能被num_heads整除assert d_model % num_heads == 0self.d_model = d_model          # 模型维度self.num_heads = num_heads      # 注意力头数self.d_k = d_model // num_heads # 每个头的维度# 定义线性变换层self.W_q = nn.Linear(d_model, d_model)  # 查询投影self.W_k = nn.Linear(d_model, d_model)  # 键投影self.W_v = nn.Linear(d_model, d_model)  # 值投影self.W_o = nn.Linear(d_model, d_model)  # 输出投影self.dropout = nn.Dropout(dropout)def scaled_dot_product_attention(self, Q, K, V, mask=None):"""缩放点积注意力的核心计算"""# 步骤1: 计算注意力分数 QK^Tscores = torch.matmul(Q, K.transpose(-2, -1))# 步骤2: 缩放scores = scores / math.sqrt(self.d_k)# 步骤3: 应用掩码 (如果提供)if mask is not None:scores = scores.masked_fill(mask == 0, -1e9)# 步骤4: Softmax归一化attention_weights = F.softmax(scores, dim=-1)attention_weights = self.dropout(attention_weights)# 步骤5: 加权求和output = torch.matmul(attention_weights, V)return output, attention_weightsdef forward(self, query, key, value, mask=None):"""前向传播"""batch_size, seq_len, d_model = query.size()# 步骤1: 线性变换得到Q, K, VQ = self.W_q(query)K = self.W_k(key)V = self.W_v(value)# 步骤2: 重塑为多头形式Q = Q.view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)K = K.view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)V = V.view(batch_size, seq_len, self.num_heads, self.d_k).transpose(1, 2)# 步骤3: 计算缩放点积注意力attention_output, attention_weights = self.scaled_dot_product_attention(Q, K, V, mask)# 步骤4: 合并多头attention_output = attention_output.transpose(1, 2).contiguous().view(batch_size, seq_len, d_model)# 步骤5: 最终线性变换output = self.W_o(attention_output)return output, attention_weights# 使用示例
def example_usage():# 模型参数d_model = 512num_heads = 8seq_len = 10batch_size = 2# 创建模型attention = MultiHeadAttention(d_model, num_heads)# 创建随机输入x = torch.randn(batch_size, seq_len, d_model)# 前向传播 (自注意力：query, key, value都是同一个输入)output, weights = attention(x, x, x)print(f"输入形状: {x.shape}")print(f"输出形状: {output.shape}")print(f"注意力权重形状: {weights.shape}")return output, weights

5.2 具体运行示例

让我们创建一个具体的例子来观察注意力权重：

def visualize_attention_example():"""可视化注意力权重的示例"""# 创建一个简单的词汇表vocab = ["<pad>", "jane", "visits", "africa", "the", "cat"]vocab_size = len(vocab)d_model = 64# 创建词嵌入层embedding = nn.Embedding(vocab_size, d_model)attention = MultiHeadAttention(d_model, num_heads=4)# 创建输入序列: "jane visits africa"input_ids = torch.tensor([[1, 2, 3]])  # [jane, visits, africa]# 获取词嵌入x = embedding(input_ids)  # (1, 3, d_model)# 计算注意力output, weights = attention(x, x, x)# 打印注意力权重 (只看第一个头)print("注意力权重矩阵 (第一个头):")print("       jane   visits  africa")for i, word in enumerate(["jane", "visits", "africa"]):row = weights[0, 0, i, :].detach().numpy()print(f"{word:>6}: {row}")return weights