无人机集群协同三维路径规划，采用冠豪猪优化器(Crested Porcupine Optimizer, CPO)实现，Matlab代码

基本介绍

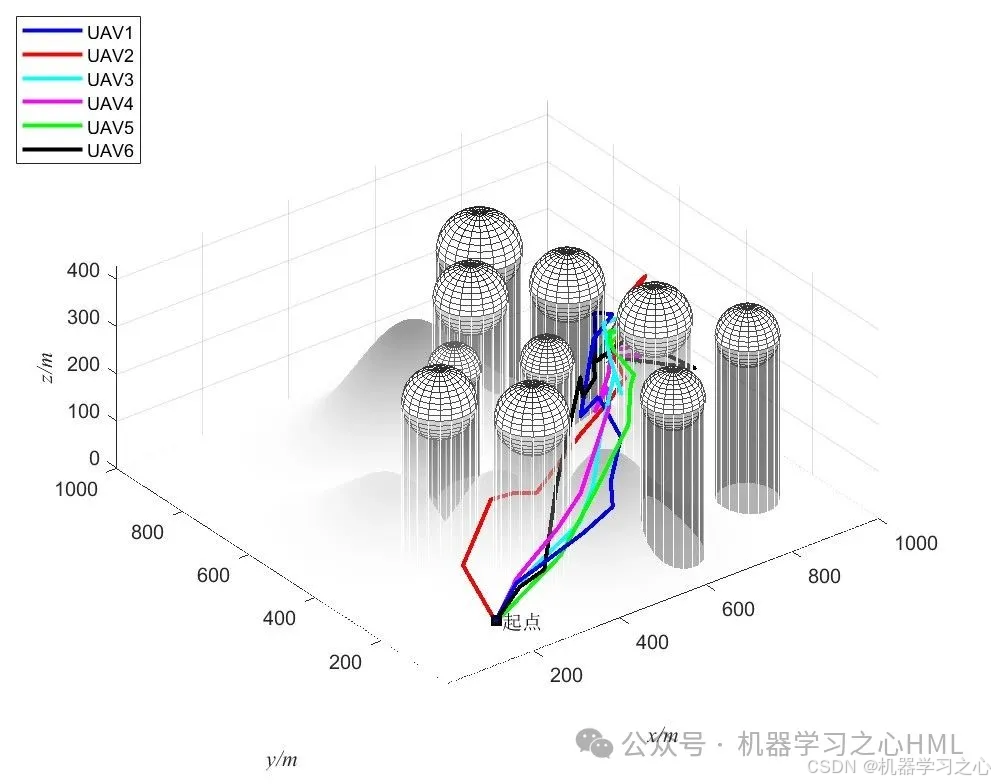
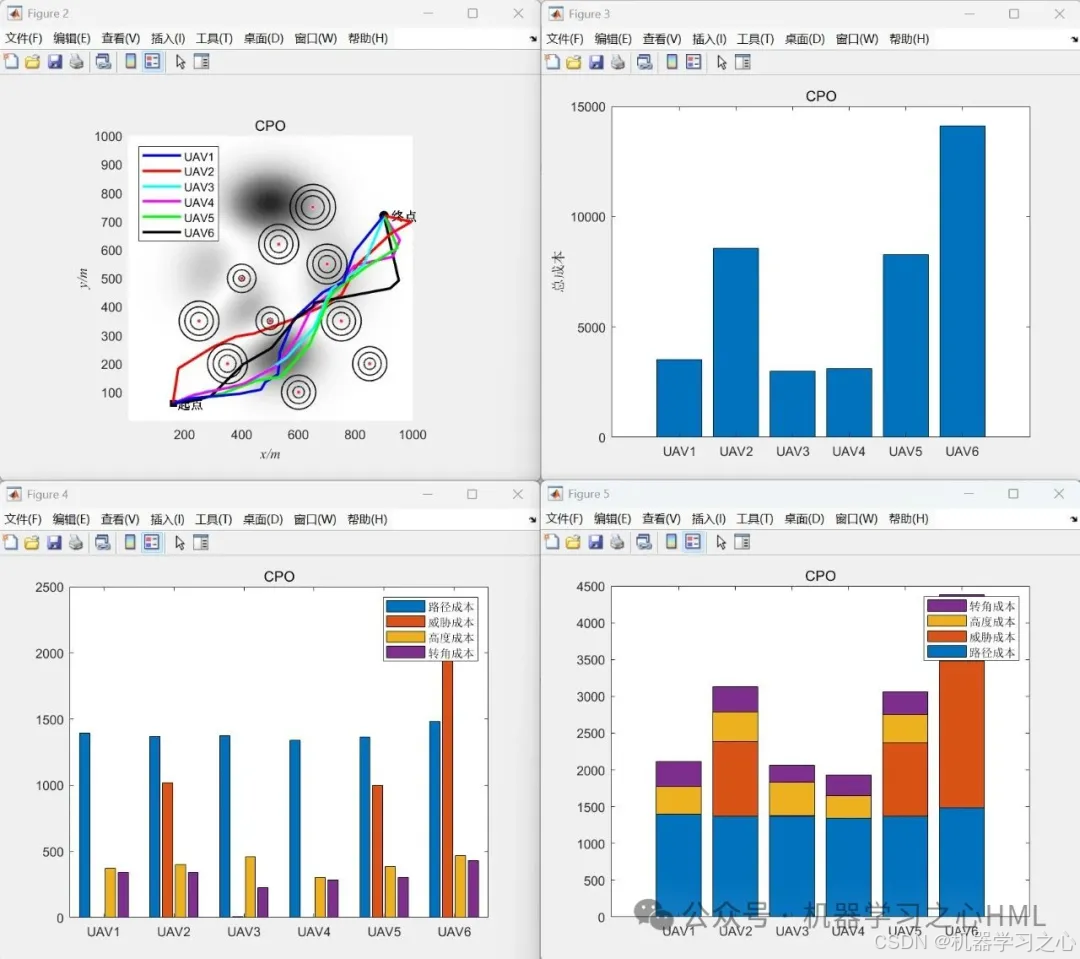
无人机集群协同三维路径规划，智能优化算法优化大揭秘！ Matlab 代码分享，不容错过！ 算法威力惊人，同时规划六个无人机！无人机集群的目标函数即为总成本，总成本为6个无人机（UAV）成本之和，每个UAV的总成本由四部分构成(路径成本、威胁成本、高度成本和转角成本)。
冠豪猪优化器(Crested Porcupine Optimizer, CPO)是一种新型的智能优化算法，该成果于2024年发表在SCI期刊Knowledge-Based Systems上。CPO算法受到冠豪猪的防御机制和觅食行为的启发，通过模拟冠豪猪的视觉、听觉、气味和物理攻击等行为，实现了对优化问题的高效求解。CPO算法的核心在于其独特的搜索机制，包括觅食阶段、群体协作阶段和自卫阶段，这些阶段共同作用，使得算法能够在复杂的搜索空间中找到最优解。

代码功能

1. main.m (主程序)

• 功能：无人机路径规划的主流程控制
• 关键步骤：
  1. 初始化环境（清除变量、添加工具箱路径）
  2. 创建地形模型(CreateModel)
  3. 获取优化问题参数(fun_info)
  4. 设置优化算法参数（种群大小100，迭代次数1000）
  5. 执行CPO优化算法
  6. 可视化路径规划结果和收敛曲线
• 输出：
  • 最优路径bestX
  • 收敛曲线convergenceCurve
  • 路径规划图

2. MyCost.m (成本计算)

• 功能：计算无人机路径的4种成本
• 成本构成：
  1. 路径长度成本(J1)：$\sum \Vert {\mathbf{p}}_{i+1}-{\mathbf{p}}_i\Vert$
  2. 威胁成本(J2)：基于点到威胁区域距离
  • 碰撞：$J_{inf}=1000$
  • 危险区：$(r_{threat}+d_{safe})-dist$
  3. 高度成本(J3)：$\sum |z_i-\frac{z_{max}+z_{min}}{2}|$
  4. 平滑成本(J4)：转弯角/爬升角变化惩罚
• 加权总成本：$cost=1\cdot J1+5\cdot J2+1\cdot J3+5\cdot J4$

3. CreateModel.m (环境建模)

• 功能：创建无人机飞行环境模型
• 建模要素：
  • 地形高程：H = 30*abs(peaks(1000))
  • 威胁区域：10个圆柱体障碍物（位置+半径）
  • 起止点：start=[160,60,50], end=[900,720,50]
  • 空间约束：
    • x∈[1,1000], y∈[1,1000], z∈[100,200]
  • 路径点数：n=10

4. Cost.m (多无人机成本聚合)

• 功能：计算多无人机系统的总成本
• 处理逻辑：
  • 单目标模式：各无人机成本直接相加
  • 多目标模式：返回[总路径长, 总威胁成本]的Pareto前沿
• 决策变量分割：$X=[X_{drone1},X_{drone2},...,X_{droneN}]$

5. fun_info.m (问题定义)

• 功能：定义优化问题参数
• 关键参数：
  • 决策变量维度：$dim=3\times n\times N$ (N=6架无人机)
  • 变量范围：
    • $r\in [0,2\Vert P_{start}-P_{end}\Vert /n]$
    • $\psi ,\varphi \in [{\varphi }_0\pm \pi /4]$ (方位角/俯仰角)
  • 目标函数：fobj = @(x)Cost(x,1)

6. SphericalToCart.m (坐标转换)

• 功能：球坐标→笛卡尔坐标转换
• 转换公式：

  x = x_prev + r·cosψ·sinφ
  y = y_prev + r·cosψ·cosφ
  z = z_prev + r·sinψ
  

• 边界处理：约束在模型空间范围内

逻辑关联图

main.m → 调用 → CreateModel (环境建模)│├→ fun_info (问题定义)│└→ CPO优化器 → 重复调用 → Cost.m → 调用 → MyCost.m│              ││              └→ SphericalToCart (坐标转换)│└→ 输出 → plotFigure (结果可视化)

算法步骤 (CPO核心流程)

1. 初始化：

   • 在球坐标空间随机生成初始种群
   • 计算各粒子的适应度(MyCost)

2. 迭代优化：

   for gen in range(maxgen):更新粒子位置(球坐标空间)坐标转换(SphericalToCart)成本评估(Cost → MyCost)更新个体/全局最优解记录收敛曲线
   

3. 结果提取：

   • 获取全局最优解bestX
   • 转换为笛卡尔坐标路径
   • 可视化飞行路径

技术路线

球坐标参数化 → 群体智能优化(CPO) → 多成本加权评估 → 路径可行性验证

关键公式原理

1. 威胁距离计算：

   • 点P到线段AB的距离：
     $dist=\frac{\Vert (B-A)\times (A-P)\Vert }{\Vert B-A\Vert }$

2. 爬升角计算：
   ${\theta }_{climb}={\tan }^{-1}\left(\frac{\Delta z}{\sqrt{\Delta x^2+\Delta y^2}}\right)$

3. 转弯角计算：
   ${\theta }_{turn}={\cos }^{-1}\left(\frac{\overrightarrow{v_1}\cdot \overrightarrow{v_2}}{\Vert \overrightarrow{v_1}\Vert \Vert \overrightarrow{v_2}\Vert }\right)$

参数设定

参数类型	参数名	值/范围	说明
环境参数	MAP_SIZE	1000×1000	地形图尺寸
	z_range	[100,200]	飞行高度范围
算法参数	pop	100	种群规模
	maxgen	1000	最大迭代次数
路径参数	n	10	单无人机路径点数
	N	6	无人机数量
成本权重	b1,b2,b3,b4	1,5,1,5	路径长/威胁/高度/平滑权重
物理约束	ψ_max	45°	最大爬升角
	φ_max	45°	最大转弯角

运行环境要求

1. 软件环境：

   • MATLAB R2023b
   • 自定义工具箱：muavbox

2. 文件依赖：

   main.m └─ muavbox/ (自定义工具箱)
   

创新点

1. 球坐标参数化：将3D路径规划转换为(r,ψ,φ)的优化问题
2. 多成本联合优化：路径长度/威胁规避/高度保持/飞行平滑性
3. 多机协同规划：6架无人机集群优化（决策变量维度=3×10×6=180）
4. 地形融合：通过高程矩阵H实现真实地形建模
5. 物理约束集成：转弯角/爬升角/飞行高度等现实约束

该解决方案实现了复杂地形下多无人机协同路径规划，通过群体智能算法在满足多种物理约束的前提下，优化飞行安全性和效率。

运行效果

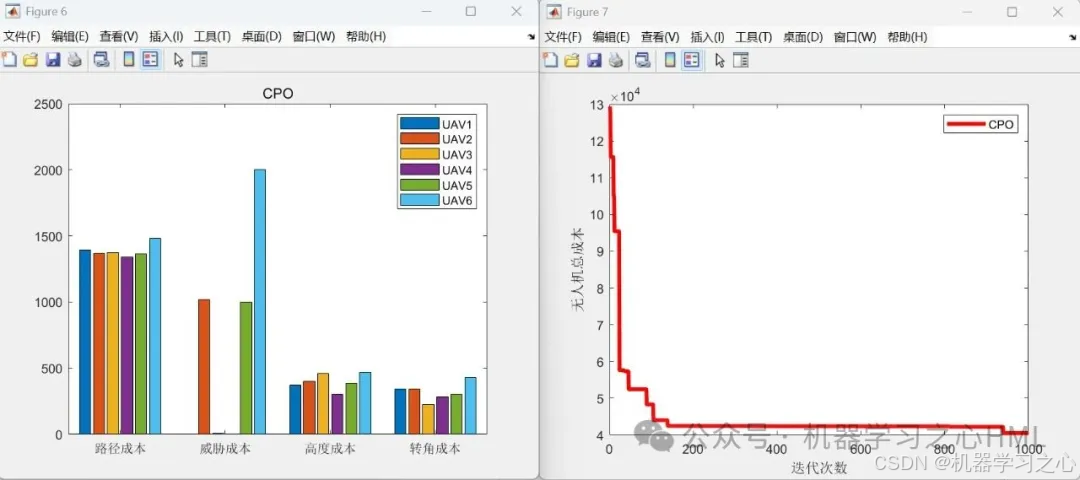
代码内容

代码获取方式1私信回复无人机集群协同三维路径规划，采用冠豪猪优化器(Crested Porcupine Optimizer, CPO)实现，Matlab代码

代码获取方式2订阅组合优化专栏后即可获取无人机集群协同三维路径规划，采用冠豪猪优化器(Crested Porcupine Optimizer, CPO)实现，Matlab代