LeetCode513：找树最左下角的值（bfs+dfs）

LeetCode 513 - 寻找树的最后一行的最左侧的值，【难度：中等；通过率：73.8%】，这道题是检验对两种核心遍历策略——广度优先搜索 (BFS) 和深度优先搜索 (DFS) 理解与运用的绝佳试金石

一、 题目描述

给定一个二叉树的根节点 root，请找出该二叉树的 最底层 最左边 节点的值

假设二叉树中至少有一个节点

示例:

示例 1:

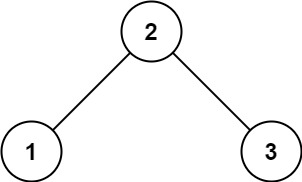
输入: root = [2,1,3]
输出: 1

示例 2:

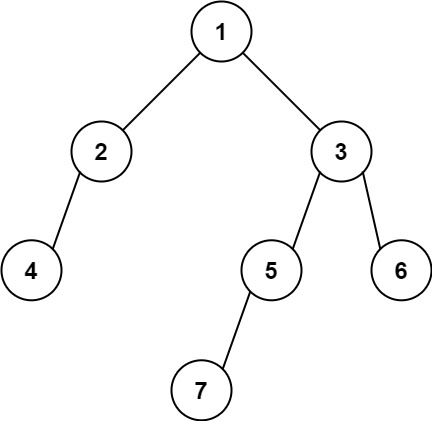
输入: root = [1,2,3,4,null,5,6,null,null,7]
输出: 7

---

解法一：层序遍历 (BFS) - 最直观的解法

既然问题涉及到“层”和“行”，那么广度优先搜索 (BFS) 无疑是最自然、最直观的解题思路。我们只需要逐层遍历，并想办法记录下每一层的第一个节点即可

核心思路

1. 使用队列进行标准的层序遍历
2. 在 while 循环中，我们知道每一次循环都将处理新的一层
3. 在开始处理这一层的所有节点之前，队列的头部元素 (queue.peek()) 正是这一层的最左侧节点
4. 我们用一个变量 resultNode 来不断更新这个“每层的最左侧节点”。当整个 while 循环结束时，resultNode 自然就指向了最后一层的最左侧节点

代码实现

class Solution {public int findBottomLeftValue(TreeNode root) {Queue<TreeNode> queue = new LinkedList<>(); // 也可自行选择其他高效实现queue.add(root);TreeNode resultNode = null; // 用于记录最终结果节点while (!queue.isEmpty()) {// 在处理本层节点前，队列的头部就是本层的最左侧节点// 用 resultNode 把它“暂存”起来resultNode = queue.peek();int levelSize = queue.size(); // 获取初始当前层的节点数量// 遍历并处理当前层的所有节点for (int i = 0; i < levelSize; i++) {TreeNode node = queue.poll();// 将下一层的节点（从左到右）加入队列if (node.left != null) {queue.add(node.left);}if (node.right != null) {queue.add(node.right);}}}// 循环结束后，resultNode 指向的就是最后一层的最左侧节点return resultNode.val;}
}

优缺点分析

• 优点：思路与问题描述高度契合，代码逻辑清晰，易于理解
• 缺点：需要使用队列，空间复杂度为 O(W)，其中 W 是树的最大宽度。对于一个茂盛的树，空间开销较大

---

解法二：递归 (DFS) - 更深度的思考

我们也可以用深度优先搜索（DFS）来解决这个问题。这里的核心思想是：如果我们能记录下每个节点的深度，那么我们只需要找到拥有最大深度的、并且最靠左的那个节点即可

核心思路

1. 定义两个全局变量：maxDepth 记录遍历过程中遇到的最大深度，resultVal 记录在最大深度下最左侧节点的值
2. 进行一次深度优先搜索（递归）。为了确保找到的是“最左侧”的节点，我们采用先序遍历的顺序（根-左-右）
3. 在遍历每个节点时，我们比较当前节点的深度 currentDepth 和已知的最大深度 maxDepth
4. 如果 currentDepth > maxDepth，这意味着我们第一次到达了一个更深的层次。由于我们是先遍历左子树，所以当前这个节点一定是这个新深度下的最左侧节点。此时，我们更新 maxDepth 和 resultVal
5. 如果 currentDepth <= maxDepth，我们不做任何操作，因为我们已经在这个深度或更深的深度找到了最左侧的节点

代码实现

class Solution {int maxDepth = -1; // 记录已发现的最大深度int resultVal = 0;   // 记录最大深度下最左侧节点的值public int findBottomLeftValue(TreeNode root) {// 从根节点开始 DFS，初始深度为 0dfs(root, 0);return resultVal;}/*** dfs* @param node  当前节点* @param depth 当前节点的深度*/private void dfs(TreeNode node, int depth) {if (node == null) {return;}// 核心逻辑：判断是否发现了新的更深层// 因为我们是先序遍历（先左后右），所以第一次到达一个新深度时，// 当前节点必然是该深度的最左侧节点if (depth > maxDepth) {maxDepth = depth; // 更新最大深度resultVal = node.val; // 更新结果值}// 搜索左子树dfs(node.left, depth + 1);// 搜索右子树dfs(node.right, depth + 1);}
}

优缺点分析

• 优点：空间复杂度仅为递归栈的深度 O(H)，对于窄而深的树，空间效率优于 BFS
• 缺点：思路相对 BFS 来说不那么直观，需要正确处理深度和值的更新逻辑

---

四、 总结与对比

	解法一 (层序遍历 / BFS)	解法二 (递归 / DFS)
核心思路	逐层遍历，不断用每层的第一个节点覆盖结果，直到最后一层	深度优先，利用遍历顺序和深度记录，找到第一个到达最大深度的节点
数据结构	队列 (Queue)	递归栈
时间复杂度	O(N)	O(N)
空间复杂度	O(W) (树的最大宽度)	O(H) (树的最大高度)
代码可读性	高，与问题描述匹配	中等，需要理解深度更新的逻辑
适用场景	解决所有与“层”相关的问题，通用性强	空间效率可能更高，尤其是在处理细长的树时