控制建模matlab练习07：比例积分控制-③PI控制器的应用

此练习主要是比例积分控制，包括三部分：
①系统建模；
②PI控制器；
③PI控制器的应用；
以下是，第③部分：PI控制器的应用。

一、比例积分控制的应用模型

1、整个系统是如图，这样一个单位反馈的形式；
2、这个系统存在扰动D(s)，因此无法直接用feedback命令来建立闭环传递函数，所以需要手动的推导。

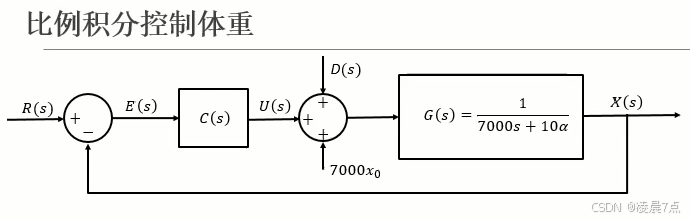
3、将整个系统的推导过程如下图，最后就能求出输入R(s)和输出X(s)之间的关系，也就得到整个系统闭环传递函数G_cl(s)。

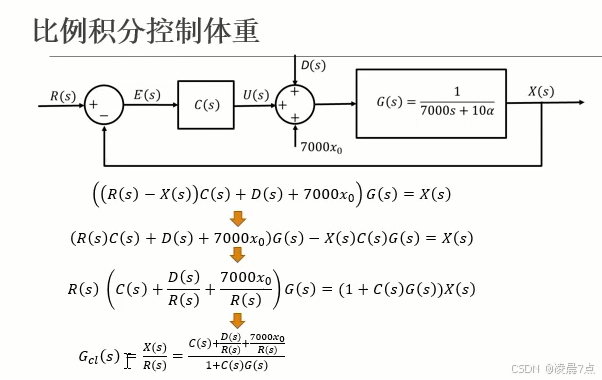
4、其中D(s)就是d(t)的表达式，进行拉普拉斯变换；
5、从练习05的案例一，这个体重作为例子：即目前体重x₀=90，准备减到目标参考值r(t)=65。

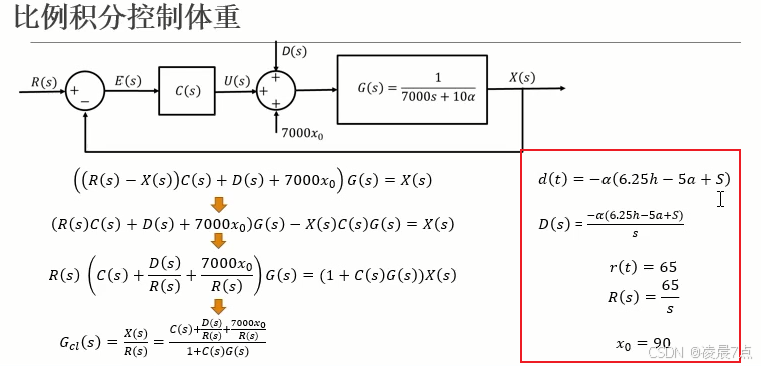
6、此时整个系统，就可以把中间这么多，看成新的闭环系统G_cls。
7、因为R(s)是常数输入，所以输出X(s)就相当于它的单位阶跃响应x对应的R倍。

clc;clear;close all;
%% 定义参数
S = 5;
x0 = [70];
h = 175;
a = 20;
Ei = [2500,2100,2500];
alpha = 1.3;
Ea = [0, 0, 500];
%% 定义G(s)
G_s = tf([1],[7000,10*alpha]);
%% 定义扰动
d = -alpha*(6.25*h-5*a+S);
D_s = tf([d],[1 0]);
%%%% 定义比例积分微分控制
kp = 200;
ki = 1; 
kd = 0;
C_s = pid(kp, ki, kd); 
%% 仿真
x0 = [90];
R_s = tf([65],[1 0]);
sys_cl = G_s*(C_s + D_s/R_s + 7000*x0/R_s)/(1 + G_s* C_s);
%% 定义输入
t = 0: 1: 3000;
R = 65;
x = R*step(sys_cl,t);%因为R(s)是常数输入，所以输出就相当于它的单位阶跃响应*对应的R倍。
plot (x);
grid on;
%%

二、运行结果及分析

1、Kp=200，Ki=1，Kd=0；
（比例积分PI结合，此时从响应速度、最后稳定值都能快速到参考值65）

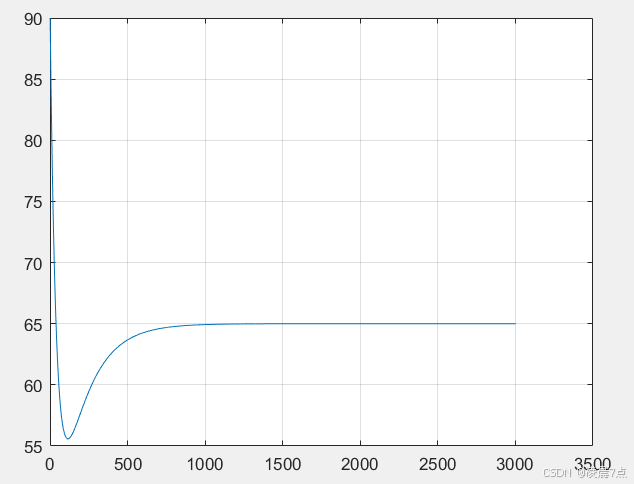
2、Kp=200，Ki=0，Kd=0；
(只有比例项P，此时无法到65，存在稳态误差)

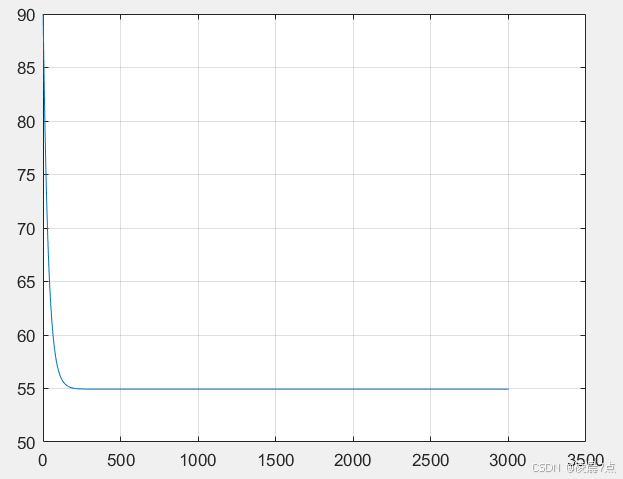
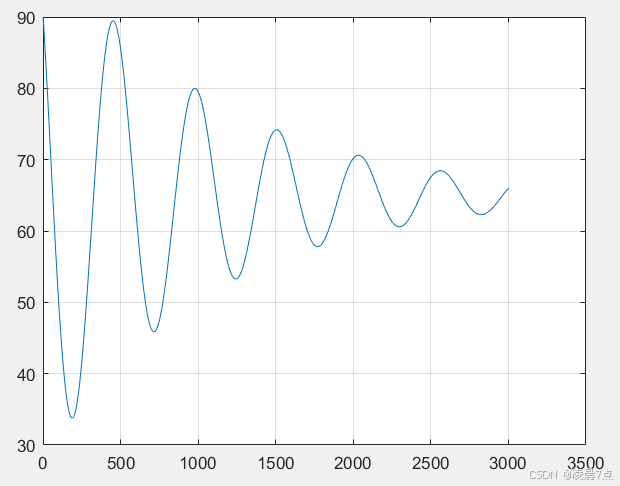
3、Kp=0，Ki=1，Kd=0；
（只有积分项I，此时存在非常大的振荡）

学习来源：《控制之美》[卷1]，王天威