深度学习周报（7.28~8.3）

目录

摘要

Abstract

1 无监督学习

2 聚类：k-means 算法

2.1 过程

2.1.1 随机初始化

 2.1.2 优化目标

2.2 选取聚类数量

3 降维：主成分分析

3.1 问题规划

3.2 算法

3.3 压缩重现

3.4 应用建议

4 总结

---

摘要

本周主要跟着吴恩达老师的机器学习系列课程学习了无监督学习及其主要的两类算法。其一是聚类，主要了解了k-means算法，包括随机初始化、优化目标与聚类数量的选择。其二是降维，主要了解了主成分分析（PCA），包括降维目标，PCA算法与应用建议等。

Abstract

This week, I primarily followed Professor Andrew Ng's machine learning series to study unsupervised learning and its two main categories of algorithms. The one is clustering, where I mainly learned about the k-means algorithm, including random initialization, optimization objectives, and the selection of the number of clusters. The other is dimensionality reduction, where I focused on Principal Component Analysis (PCA), covering the objectives of dimensionality reduction, the PCA algorithm, and application guidelines.

1 无监督学习

前两周学习的SVM算法属于监督学习。其中监督学习是一种机器学习范式，在监督学习中，算法通过学习从输入到输出的映射关系来进行训练，每个用于训练的数据都有与之对应的标签。除了SVM，前面学习的分类与回归也属于监督学习。

与之相对的另一种机器学习范式是无监督学习，在无监督学习中，算法从不含标签的数据中学习其结构或模式，主要包括聚类算法、降维算法、自编码器等等。

除了上述两种，机器学习范式还包括自监督学习、半监督学习、强化学习与迁移学习等。

无监督学习非常适合于那些难以获取大量标注数据的任务。例如，其中聚类算法主要的应用就包括：组织大型计算机集群高效协作、社交网络分析、市场分割与天文数据分析等等

2 聚类：k-means 算法

聚类算法，顾名思义，就是将类似的东西聚在一起。其中运用最广泛的是k-means算法，它也叫k均值算法，这是一种迭代算法，它的输入包括聚类数量与所有无标签的输入数据。

2.1 过程

其过程大致如下：

1.随机生成几点作为聚类中心，数量与聚类数量相同；

2.簇分配：将所有点按照到聚类中心的远近进行分类 ；

3.移动聚类中心至所有同类点的均值位置；

4.重复2、3操作直至聚类中心位置不再改变。

如下图：绿点代表无标签数据，红叉和紫叉代表初始生成的两个聚类中心。遍历所有绿点，看与红色中心更近还是紫色更近，然后分别染成相应颜色。

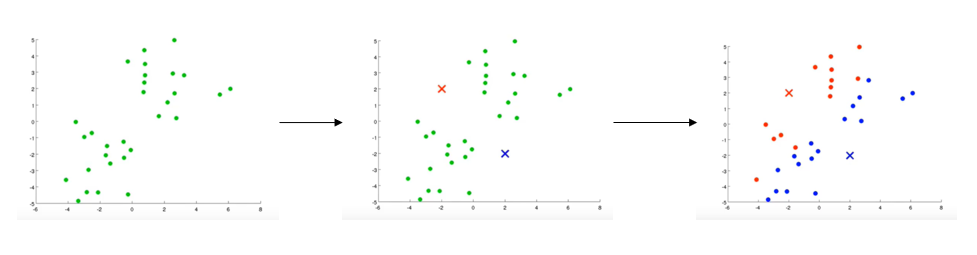
如果存在一个没有点的聚类中心，则可以直接移除它。比如，若上图中还生成了一个黄色的聚类中心，但所有数据均被分配到红色与紫色的聚类中心，那么可以直接移除黄色聚类中心

2.1.1 随机初始化

随机初始化指的是算法第一步，随机生成K个聚类中心，即，随机选择K个样本，使聚类中心位置与它们一样。通常来说，聚类中心数小于样本数（大于，产生空类，后续会被移除；等于，一个样本就是一个类，没有太大意义）。

下图是对于同样的数据，两种不同的随机初始化：

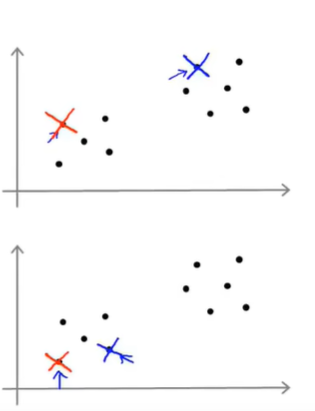
随机初始化不同，最终结果也可能不同。如果随机初始化得到的结果不好，就可能得到不同的局部最优解，如下：

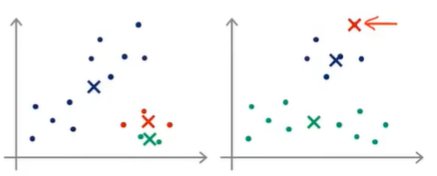
为了避免陷入局部最优，可以尝试进行多次随机初始化，然后选择代价最小的，但这种方法也不一定能够改善（比如当K非常大时，…）

 2.1.2 优化目标

k-means 算法的代价函数也叫失真代价函数或者k均值算法的失真。其公式如下：

其中  代表当前样本（  ）所属簇的索引号或者序号； 表示第  个聚类中心的位置（k大写表示聚类数量，小写代表具体的某个聚类中心）；  代表当前样本（  ）所属簇的聚类中心。

在簇分配时，由于聚类中心的位置固定不变，所以对每个样本都要选择合适的  来使失真函数最小；在移动聚类中心时，每个样本已经分配好对应的簇，要根据它们来选择合适的  来使失真函数最小。

2.2 选取聚类数量

在聚类数量的选择问题上，现在还没有自动的算法可以辅助，一般还是通过观察可视化的图或者输出来手动选择。

手动选择可以依据肘部法则。因为随着聚类数量的增加，代价值会降低，通常在某个点之前快速下降，之后缓慢下降（如下图左），这个拐点对应的聚类数量就是肘部法则所选的聚类数量。但肘部法则并不常用，因为在实际运用中，曲线会较为光滑，没有清晰的拐点，如下图右。

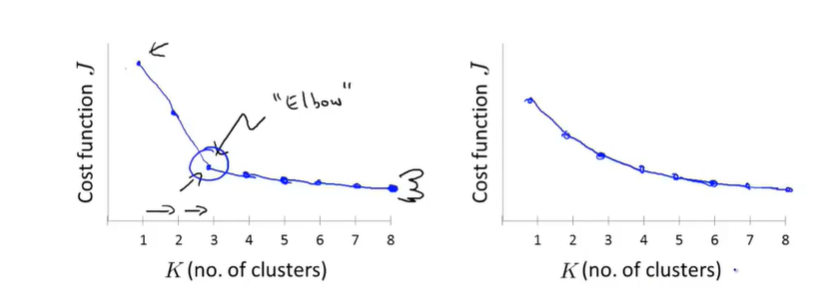
k-means 算法的主要功能是对数据进行聚类，属于数据处理的上游算法，所以为了适应下游的应用需求之类，可以也更推荐根据后续目的来选择聚类数量。

3 降维：主成分分析

无监督学习的另一类重要算法是降维，其思想主要是减少数据的复杂性，同时尽可能保留数据中的关键信息。其中运用最广泛的是主成分分析。

降维的一个主要目标是对数据进行压缩，这样能够减少数据所占用的内存空间，还能加速学习算法；另一个则是方便可视化，使得高维数据可以在二维或三维空间中可视化，这对于理解数据结构和模式非常有帮助。

以将数据从二维降到一维为例。下图中，横纵坐标分别代表厘米与英寸，这两个特征实际上都是对物体长度进行描述，那么可以将它们投影到一条直线上进行降维。

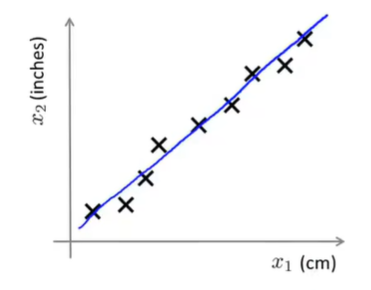
相应的从三维降到二维则需要投影到平面。

3.1 问题规划

PCA会找一个低维平面，然后将数据投影到这个平面，并尽量最小化投影误差。如果想将数据从n维降到k维，就需要找到k个方向向量对数据进行投影来最小化投影误差。下图中，显然红色方向向量比粉色方向向量的投影误差要小。

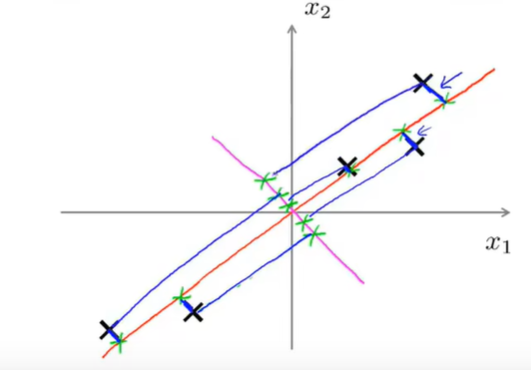
另外应用PCA之前，需要先进行标准化或特征规范化，使得其数值在可比的范围之内。

PCA与线性回归是不一样的。线性回归是拟合一条直线来最小化点与直线之间的平方误差，而PCA试图最小化的是投影误差，表现在图像上即线性回归计算误差的方向与y轴平行，而PCA与方向向量垂直，如下图；且线性回归是用特征（x）对标签（y）进行预测，而PCA只有特征（x）。

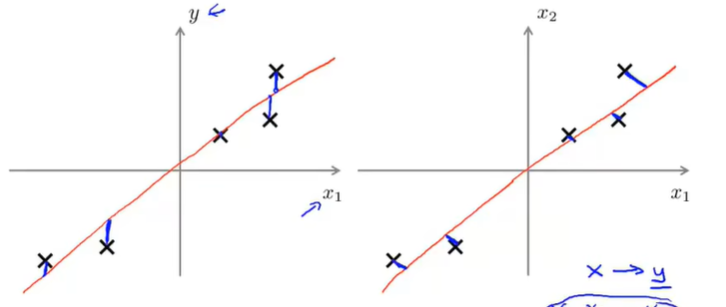
3.2 算法

首先对数据进行预处理，即进行标准化：

其次，计算数据的协方差矩阵以反映特征之间的线性相关性：

该矩阵通常为对称、半正定矩阵，  表示第  和第  个特征之间的协方差。当  时，它代表第  个特征的方差。

然后，解如下方程以得到协方差矩阵的特征向量，即数据变化最大的方向（主成分），对应的特征值表示该方向上的方差大小。

其中  为特征值， 代表对应的特征向量。

最后选择主成分，将特征值按照从大到小的顺序排列，选择前  个构成投影矩阵，以实现降维。

另外，还涉及到两个概念。一个叫解释方差比例，其公式如下：

另一个是累计解释方差比例，其公式如下：

累计解释方差比例代表着保留信息的程度，通常在80%~95%左右，这是选择  的重要依据。

3.3 压缩重现

既然能降维，对数据进行压缩，自然也应该可以复现数据。这个过程也叫原始数据的重构。其公式如下：

 为  维，是前  个主成分组成的投影矩阵， 为  维，是压缩后每个样本对应的特征向量。

如果投影误差不大，那么  会非常接近 原先用来求  的 。

3.4 应用建议

首先，PCA定义了一个从x到z的映射，这个映射只能通过在训练集上拟合的PCA来定义，可以应用于交叉验证集和测试集样本中。PCA不能在整个数据集上进行拟合，会造成数据泄露，导致评估不公正。

其次，PCA不能用来防止过拟合。虽然它减少了特征数量，但始终是一种无监督方法，并不考虑标签y。

防止过拟合的首选方法还是前面学习的正则化。PCA 主要是为了加速计算和可视化。

最后，在实现PCA以前，首先应该考虑使用原始数据进行训练。只有在使用原始数据无法达到目的时才考虑使用PCA，这样能够避免潜在的损失。

4 总结

本周主要学习了k-means算法与PCA两个无监督学习的重要算法，学习了它们的原理，但感觉对PCA的了解还有点模糊。下周计划首先通过代码实践或者具体理清对PCA的理解，然后开始异常检测部分的学习。