译|用户增长策略如何使用因果机器学习的案例

来自上传文件中的文章《[Causal Machine Learning for Growth: Loyalty Programs, LTV, and What to Do When You Can’t Experiment | by Torty Sivill | Towards AI]》
本文探讨了当 A/B 测试不可行时，如何利用因果推断从历史数据中获取洞察。技术亮点在于通过构建反事实世界来估计处理效应，并强调了混杂变量的重要性。文章介绍了在已知因果结构下使用线性回归进行因果效应估计，以及在未知结构下利用 NOTEARS 等因果发现算法推断因果图。该方法适用于无法进行随机实验的场景，例如评估忠诚度计划对客户生命周期价值的影响，或处理混杂因素复杂的庞大数据集。

---

---

这是一个关于用反事实推理取代 A/B 测试的实践指南。

图片来自 Mathieu LESNIAK, Unsplash

很明显，因果推断正变得越来越重要。那些严重依赖实验的公司现在面临着 A/B 测试不可行、不切实际甚至适得其反的情况。他们正在寻找替代方法，从现有数据中获取因果洞察。

让我们以一家假日预订公司为例，这是一种实验深度嵌入的业务。增长或留存团队可能会问一个关键问题：

我们的忠诚度计划对客户生命周期价值 (LTV) 有何影响？

这是一个经典的“处理效应”场景：一些用户加入了忠诚度计划，我们想知道这如何影响他们未来的消费。

为何我们无法对忠诚度计划进行 A/B 测试？

1. 公平性和风险：随机地对一半客户不提供忠诚度计划，尤其是包含折扣或福利的计划，这感觉很不道德。声誉成本太高。
2. 时间跨度：LTV 是按月或按年衡量的。等到测试结束时，产品、用户行为或市场条件可能已经发生变化，导致结果过时。
3. 自愿加入性质：忠诚度计划不是用户可以被强制分配的。实际上，用户是自愿选择加入该计划的，而选择加入的用户很可能是常旅客、更富有且参与度更高。这意味着他们更高的 LTV 可能归因于他们本身的特质，而非计划本身。

所以现在我们陷入困境。我们无法运行实验，但我们确实有一个装满历史数据的仪表板……

因果推断作为替代方案

这就是因果推断发挥作用的地方。我们不进行实时实验，而是使用历史数据来估计如果用户没有加入忠诚度计划会发生什么。

在 A/B 测试中，随机化确保混杂变量（例如财富、旅行频率）在处理组和对照组之间均匀分布。这样，结果的任何差异都可以归因于处理。

但对于观测数据，这种平衡并不存在。因此，因果推断背后的思想是重建一个反事实世界，一个通过使用来自相似用户的合成对照，将忠诚度计划用户与他们如果没有加入该计划的 LTV 进行比较的世界。

构建模拟数据集

为了演示其工作原理，我们创建了一个合成数据集，该数据集捕获了我们的假日预订示例。

import pandas as pd  
import numpy as np  
from sklearn.preprocessing import StandardScaler  
from linear import notears_linear  n = 1000  
np.random.seed(42)  
past_bookings = np.random.poisson(lam=3, size=n)  
average_booking_value = np.random.normal(loc=400, scale=100, size=n)  
is_high_income = np.random.binomial(1, p=0.3, size=n)  
channel = np.random.choice(["email", "ads", "organic"], size=n)  
channel_encoded = pd.get_dummies(channel, prefix="channel")loyalty_score = (  0.4 * past_bookings +  0.003 * average_booking_value +  1.0 * is_high_income +  0.5 * (channel == "email").astype(int)  
)  
p_loyalty = 1 / (1 + np.exp(-loyalty_score / 5))  
loyalty_enrolled = np.random.binomial(1, p_loyalty)lifetime_spend = (  100 * past_bookings +  0.8 * average_booking_value +  300 * loyalty_enrolled +  500 * is_high_income +  np.random.normal(0, 200, n)  
)df = pd.DataFrame({  "past_bookings": past_bookings,  "average_booking_value": average_booking_value,  "is_high_income": is_high_income,  "loyalty_enrolled": loyalty_enrolled,  "lifetime_spend": lifetime_spend  
})  
df = pd.concat([df, channel_encoded], axis=1)  
df

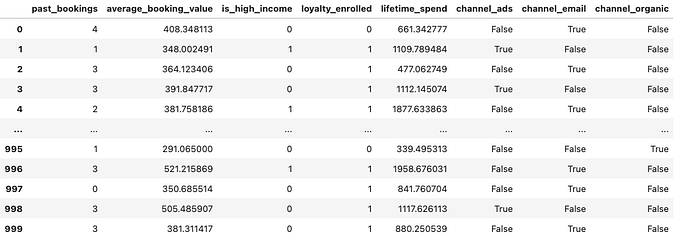
作者生成图片。表格显示了假日预订公司示例的生成数据集。

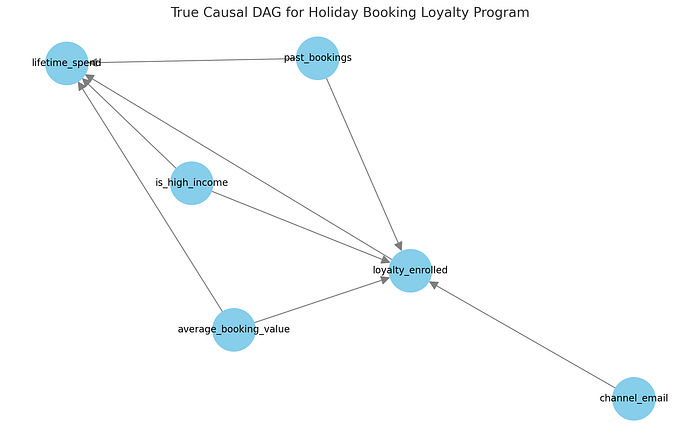
预订公司示例的真实因果图。

在我们的数据生成过程中：

• past_bookings（过去预订量）、average_booking_value（平均预订价值）和 is_high_income（是否高收入）等变量会影响加入忠诚度计划的可能性以及总客户消费。这些是我们的混杂因素。
• 忠诚度计划本身对客户生命周期消费有因果效应，这是我们想要估计的。
• 营销渠道（例如 channel_email）可能会影响计划注册，但不一定会影响未来消费。

我们使用这种结构来模拟数据，模拟真实业务中可能出现的历史客户行为。这为我们提供了一个清晰的环境来探讨两个问题：

1. 如果我们知道真实的因果结构，将如何估计忠诚度注册的因果效应？
2. 如果我们不知道，并且必须使用 NOTEARS 等技术从数据中推断结构，又该如何？

使用已知因果图确定因果效应

在这里，我们很幸运地自己生成了数据，因此可以轻松提取真实的因果结构。然而，对于描述真实世界系统的真实数据，我们需要尝试自己构建因果图。

因此，大量精力投入到首先理解问题的因果结构上。目标是得到一个因果图——一个变量如何相互影响的模型——它决定了必须调整哪些变量才能无偏估计因果效应。

一旦你有了这个图（或一个合理的近似），你就可以使用标准统计工具来估计因果效应。例如：

adjustment_vars = ["past_bookings", "average_booking_value", "is_high_income", "channel_email"]  
X = df[adjustment_vars + ["loyalty_enrolled"]]  
y = df["lifetime_spend"]model = LinearRegression().fit(X, y)  
print("Estimated effect of loyalty program (NOTEARS-adjusted):", model.coef_[-1])

乍一看，线性回归可能看起来像一个预测工具，确实如此。但当与因果图结合使用时，它也可以为我们提供处理效应的因果估计，在本例中是忠诚度计划注册对客户生命周期消费的影响。

关键在于混杂。混杂变量是同时影响处理（加入忠诚度计划）和结果（某人消费多少）的变量。如果我们不考虑混杂变量，我们就无法判断观察到的效应是由于处理还是仅仅是相关的背景因素。

在因果推断中，我们旨在通过调整混杂变量来阻断所有后门路径：处理和结果之间间接的、非因果的路径。这被称为后门调整准则。

在我们的回归模型中，我们根据因果图包含了所有已知的混杂变量。这意味着我们正在比较那些在过去预订量、收入和获取渠道方面相似，但仅在是否加入忠诚度计划方面不同的用户。然后，回归估计了那些加入计划的用户平均多花了多少钱，同时控制了所有其他因素。

这就是为什么 loyalty_enrolled 上的系数是一个因果效应估计，而不仅仅是相关性。

当然，这仅在以下情况下成立：

• 我们正确识别并包含了所有相关的混杂变量。
• 背景中没有主要的未测量混杂变量。

如果这些假设成立，线性回归就成为一个强大的、可解释的工具，用于估计因果效应，即使在没有 A/B 测试的情况下也是如此。

飞行员注册对 LTV 的因果效应估计。

平均而言，在控制了混杂因素后，加入忠诚度计划的用户在 12 个月内比未加入的用户多花费了约 £315.81。

如果你甚至不知道哪些变量是混杂变量怎么办？

也许你的数据量巨大、杂乱，并且充满了客户特征：你不确定哪些是混杂变量，哪些不是。

因果发现来救援

这就是因果发现工具的用武之地。因果发现是机器学习中一个相对较新（且令人兴奋）的分支，它试图根据一组数据找到最佳的因果图。其中一种方法是 NOTEARS，这是 Zheng 等人于 2018 年在卡内基梅隆大学提出的一种因果发现算法。

NOTEARS 学习一种特殊类型的因果图，即 DAG（有向无环图），这意味着该图中的每条边都有一个方向，并且没有循环（这在因果关系中非常重要，因为事物不能既是原因又是结果！）。

学习 DAG 是非常困难的，因为符合数据的可能图空间是组合爆炸的（非常非常大）。这意味着测试所有可能的图是不可能的。更糟糕的是，检查图中的循环是不可微分的（因此不能使用基于梯度的常规机器学习方法）。

由于我们无法遍历所有可能的因果图，因此因果发现方法必须采用更具计算优雅性的方式来发现最符合数据的因果图。许多方法使用基于启发式的搜索。

NOTEARS 根本不搜索 DAG 空间，它通过一个巧妙的技巧学习因果图，该技巧将离散搜索转换为连续优化问题。这意味着可以使用基于梯度的求解器。

使用 NOTEARS 进行因果效应估计

对我们来说幸运的是，我们不必自己实现 NOTEARS，我们可以克隆原始仓库，然后简单地像这样导入：

from linear import notears_linear    features = df[[  "past_bookings", "average_booking_value", "is_high_income",  "channel_ads", "channel_email", "channel_organic",  "loyalty_enrolled", "lifetime_spend"  
]]  
X = StandardScaler().fit_transform(features)  
W_est = notears_linear(X, lambda1=0.01, loss_type='l2')

然后我们可以使用这个邻接矩阵来可视化 NOTEARS 推断出的因果图。

import matplotlib.pyplot as plt  
import networkx as nxadj_matrix = pd.DataFrame(W_est, index=features.columns, columns=features.columns)  
G = nx.DiGraph()  
threshold = 0.3  
for i, src in enumerate(adj_matrix.index):  for j, tgt in enumerate(adj_matrix.columns):  if abs(W_est[i, j]) > threshold:  G.add_edge(tgt, src, weight=W_est[i, j])plt.figure(figsize=(12, 7))  
pos = nx.spring_layout(G, seed=42)  
nx.draw(G, pos, with_labels=True, node_color='skyblue', node_size=2000,  edge_color='gray', font_size=10, arrowsize=20)  
plt.title("Inferred Causal DAG (NOTEARS)", fontsize=14)  
plt.tight_layout()  
plt.show()

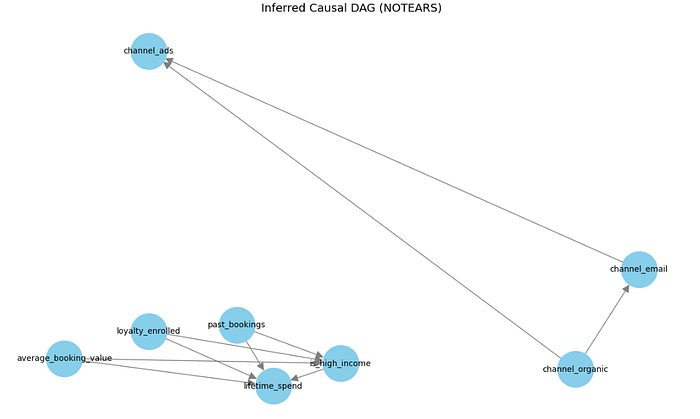
NOTEARS 在预订公司示例上学习到的因果图。

有趣的是，在 NOTEARS 推断出的因果图中，loyalty_enrolled 似乎是一个根节点，没有来自任何其他变量的入边。这表明，在该图下，处理和结果之间没有混杂因素。

如果这是真的，我们就不需要调整任何东西：忠诚度注册和客户生命周期消费之间观察到的关系可以被解释为因果关系，而无需任何控制。

然而，这与已知的数据生成过程相矛盾。在我们的模拟中，past_bookings 和 is_high_income 等变量显然影响注册和消费，使它们成为混杂因素。

如果我们使用这个因果图来确定忠诚度计划注册对 LTV 的因果效应，我们将得到一个被高估的估计，虽然方向正确，但被混杂因素严重夸大。

treated_mean = df[df["loyalty_enrolled"] == 1]["lifetime_spend"].mean()  
control_mean = df[df["loyalty_enrolled"] == 0]["lifetime_spend"].mean()  
unadjusted_effect = treated_mean - control_meanprint(unadjusted_effect)

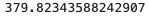
因果发现的局限性

因果发现的强大程度取决于其背后数据的质量。噪声、有限的样本或模型偏差可能导致遗漏依赖关系和不完整的图。这就是为什么在选择调整集时，将算法与领域知识结合起来至关重要。

这种局限性或许是因果发现尚未广泛应用的原因。许多团队缺乏手动定义因果结构的时间或工具。更好的自动化发现将使因果推断更易于访问，而这正是 AI 可以提供帮助的地方。

在 Decima2，我们开发了强大而准确的基于 AI 的因果发现算法。