LQR个人笔记

1.最优控制算法

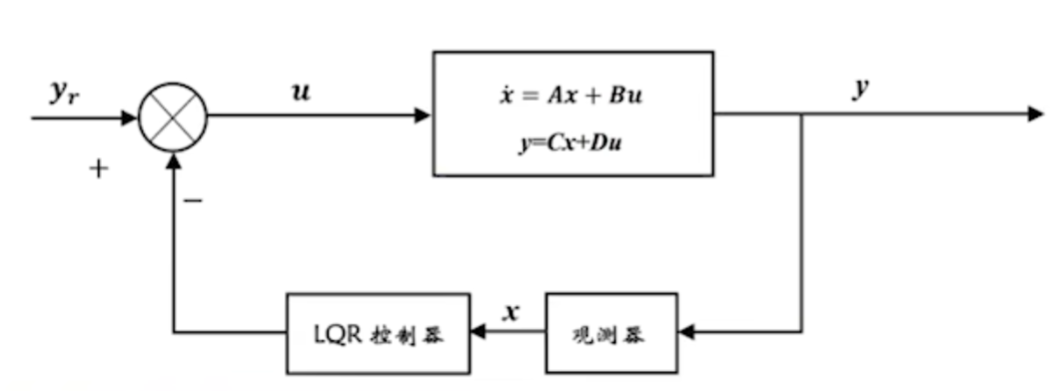
2.优缺点：

（1）必须是线性时不变模型（2）是多输入多输出的，是使用了状态空间方程的模型，相比于PID的优点（3）最小代价函数可以计算出能量最优的方式使得系统稳定下来（4）需要实时的计算相应的矩阵：状态反馈矩阵和控制增益

3.深入原理：

（1）相比于PID的输出反馈，他是状态反馈控制，回顾之前信号与系统学的系统框图内容，对于输入u输出y的描述往往会引入x即状态变量进行描述。而LQR就是使用x进行反馈回到u里面而不是直接用y反馈到u。然后由于引入了反馈，u可以用x表示。所以原先的状态方程可以改写成只有x，y两个量。而且可以多状态反馈

（2）反馈量-K里的K也叫增益矩阵，u=-Kx

（3）代价函数J：，Q和R是权重矩阵， Q 必须是半正定矩阵，即所有对角元素 q_ii 必须大于等于零， R 必须是正定矩阵，正定性要求所有对角元素 r_kk 必须严格大于零。非对角元素可负表示状态分量间的特殊耦合惩罚，一般忽略即设为0。增大对于x的权重会使得收敛速度更快，LQR就是为了使得J最小，且由于QR的正定性会使得带来的一定是非负的惩罚，J大于等于0。

（4）黎卡提方程：用于在J的基础上求出K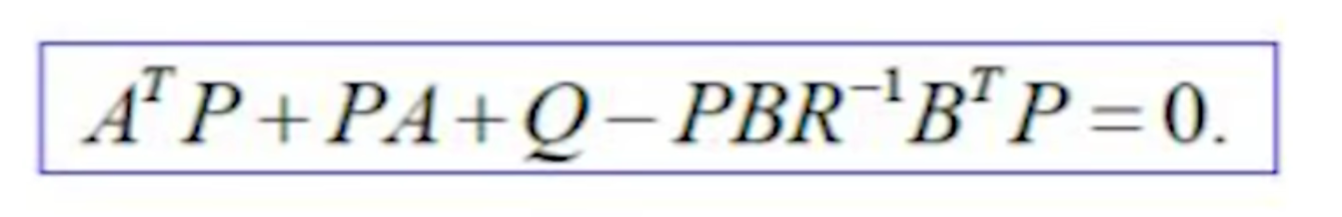

（5）观测器的作用：显然用lqr需要每个x状态变量，但是有些状态变量不能直接从传感器读出，如果要通过微分积分得到噪声会很大，所以需要观测器去估计

4.matlab：

（1）tf2ss：将传递函数转化成状态方程，或者直接写出来

（2）手动配置QR权重，Q看阶数，即s是几次方，R看u的维度

（3）调用lqr函数得到K

（4）仿真时可以用卡尔曼观察器，好像还有极点配置法可能出反馈量需要的x。

（5）调参：K是根据代价函数来的因此QR配置很关键，基于对于权重越大收敛越快（趋于0），所以增大R了，u更快的变小，输入变小了，响应的时间也会变长，意味着使用大的控制量成本越高，控制器会更倾向于使用较小的控制输入。至于Q的作用就是人对应趋于01，有说法称为原点x=0，Q越大越快拉回原点。

5.最后现象：

由于引入反馈：y = Cx + D(-Kx) = (C - DK)x。矩阵 (𝐶−𝐷𝐾)(C−DK) 决定哪些状态分量对输出影响更大（例如传感器测量位置），但无法改变系统固有动态（极点）。

原先开环增益A（s）也会变成闭环增益G（s）因此K还会影响闭环系统的极点，通常配置为左半平面

，由闭环状态方程：x(t)=Ax(t)+B(−Kx(t))=(A−BK)x(t)，极点是A−BK的特征值

---

上面的讲述大致就是网络上常见的概念了，但是还是太浅了，远远没到应用的地步，因此再作补充：

1.通常情况下我们接触到的都是开环系统，如果输入油门，偏航，得到位置，角度等，像这样的多输入多输出系统。这种开环系统显然我们可以得到其状态方程和输出方程。这就是前文提到的第一步，ABCD矩阵的由来

2.这个时候往往会发现运动很飘很不丝滑或者达不到想要的效果，所以引入闭环控制改善系统增益函数变成闭环增益。

3.对于多变量系统的稳定性，LQR首先把输入置为0了。再去引入反馈，这个时候输入完全由反馈量x决定也就是u=-Kx。再进行后续一系列推导，使得u，x，y均稳定，且把稳定的设置0点，即J非负还要最小的原因，LQR是专注与系统稳定的算法。标准的LQR是不允许输入其他信号的。

4.想要输出非0的y怎么办？引入输出反馈控制，使得u变为=-Kx+新反馈量比如误差积分。其实只要改变u=-Kx就好，另外如果引入的反馈量不涉及状态变量，A-BK的极点稳定性是会保留的，这就是为什么LQR可以用来稳定PID。

5.显然引入了新输入后，x，u将会不再稳定在0点。