【MATLAB】(四)函数运算
MATLAB函数计算
除了简单的依靠运算符进行MATLAB四则运算,MATLAB还包括复数运算、三角函数和指数运算等运算。
1.复数运算

(1)复数的加减乘除
>> %复数运算>> x=1+2i;
>> y=3+5i;
>> x+yans =4.0000 + 7.0000i>> x-yans =-2.0000 - 3.0000i>> x*yans =-7.0000 +11.0000i>> x/yans =0.3824 + 0.0294i(2) 复数构造的两种方式
>>%构造复数
>> complex(1,2)ans =1.0000 + 2.0000i>> 1+2ians =1.0000 + 2.0000i>> x=1+2i;(3)判断复数是否为实数
>>%判断是否是实数(虚部是否为0)
>> isreal(x)ans =logical0>> x=1x =1>> isreal(x)ans =logical1
(4)求复数的相角和复数的模
复数的一般代数形式为z = a + bi,其中 a 为实部,b 为虚部,i 为虚数单位(满足 i^2 = -1)。 在复平面中(横轴为实轴,纵轴为虚轴),每个复数都对应一个坐标为 (a, b) 的点,也可以看作从原点出发到该点的向量。此时:
复数的模(Modulus)是这个向量的长度,即 |z| = sqrt(a^2 + b^2);
复数的相角是这个向量与实轴正方向的夹角,通常用符号 arg(z) 表示,单位为弧度rad或度°。
>> x=complex(1,1)x =1.0000 + 1.0000i>> angle(x)ans =0.7854
>>%位角是45°,也就是Π/4,所以是0.7854
>> abs(x)ans =1.4142
(5)求复数的实部,虚部以及共轭
>> x=complex(1,2)x =1.0000 + 2.0000i>> real(x)ans =1>> imag(x)ans =2>> conj(x)ans =1.0000 - 2.0000i2.三角函数运算
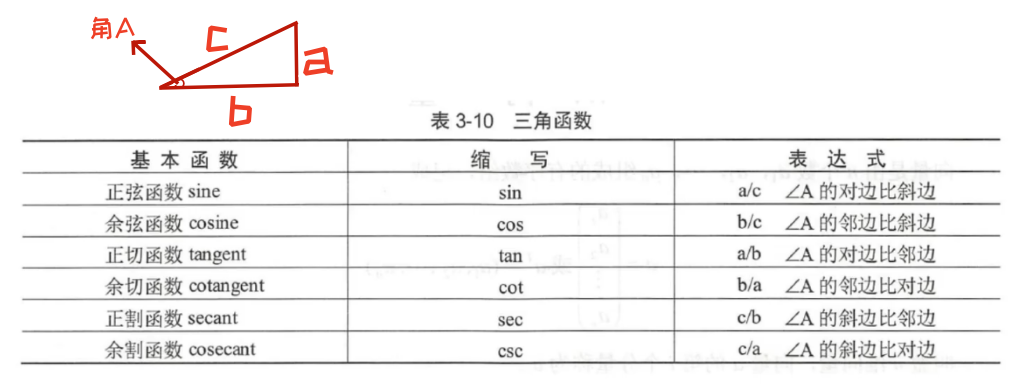
(1)根据角度求三角函数---sin、cos和tan
>> sin(pi)ans =1.2246e-16>> cos(pi)ans =-1>> epsans =2.2204e-16其中,sin(pi)=1.2246e-16=eps,是matlab中近似表示0的一种形式。
(2)根据三角函数值求角度---asin、acos和atan
>> asin(1)ans =1.5708>> acos(1)ans =0>> atan(1)ans =0.7854
其中,pi=3.14159,pi/2=1.5708,pi/4=0.7854
-------------------------------------------------------------------
编自2025/8/2。科目二二战也是一把过了=v=歌手也看爽了,继续听课了。
