人工智能之数学基础:离散型随机事件概率(古典概型)
本文重点
前面我们学习了频率和概率,概率可以理解为衡量某个事件发生的可能性。本文将学习概率中经典的古典概型,它是一种特殊的古典概率模型。
古典概型
如果对于一个试验满足以下的两个条件,那么就可以称这样的模型为古典概型:
1.实验结果是有限的
2.各种结果出现的可能性相同
如果我们将试验结果记为w1,w2,...,wn,则总样本
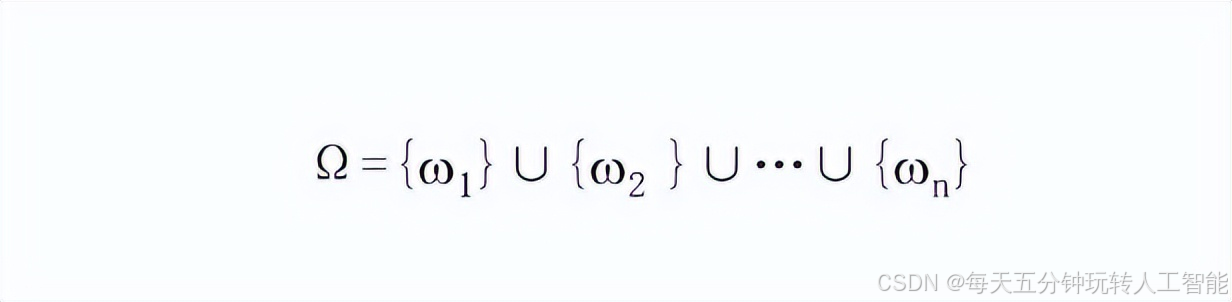
其中每一个{wi}都是基本事件,并且两两互斥,而且重要的是每个基本事件发生的概率相等。他们之间的概率相加为1:
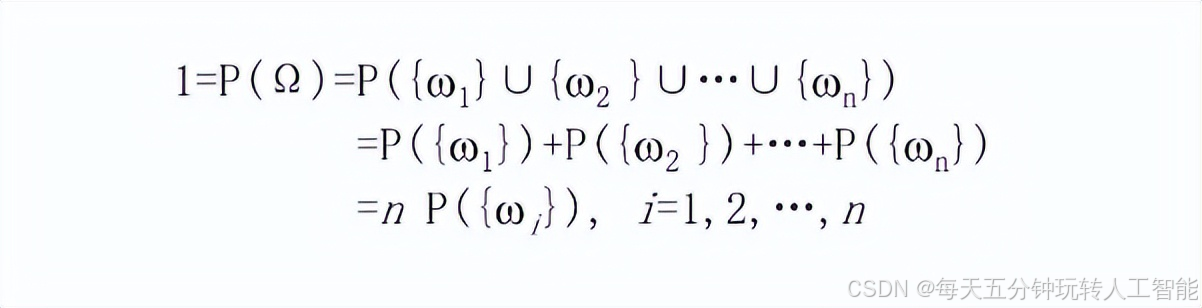
也就是说每一个基本事件wi,发生的概率都是p(wi)=1/n
古典概型的作用
当一个随机试验符合古典概型的时候,我们必须记住每一个基本事件发生的概率相等,这样如果我们要是想要评判一个事件A发生的概率,我们只需要计算事件A中包含多少个基本事件,然后P(A)=A中的基本事件数/该随机试验的总事件数
