5734 孤星
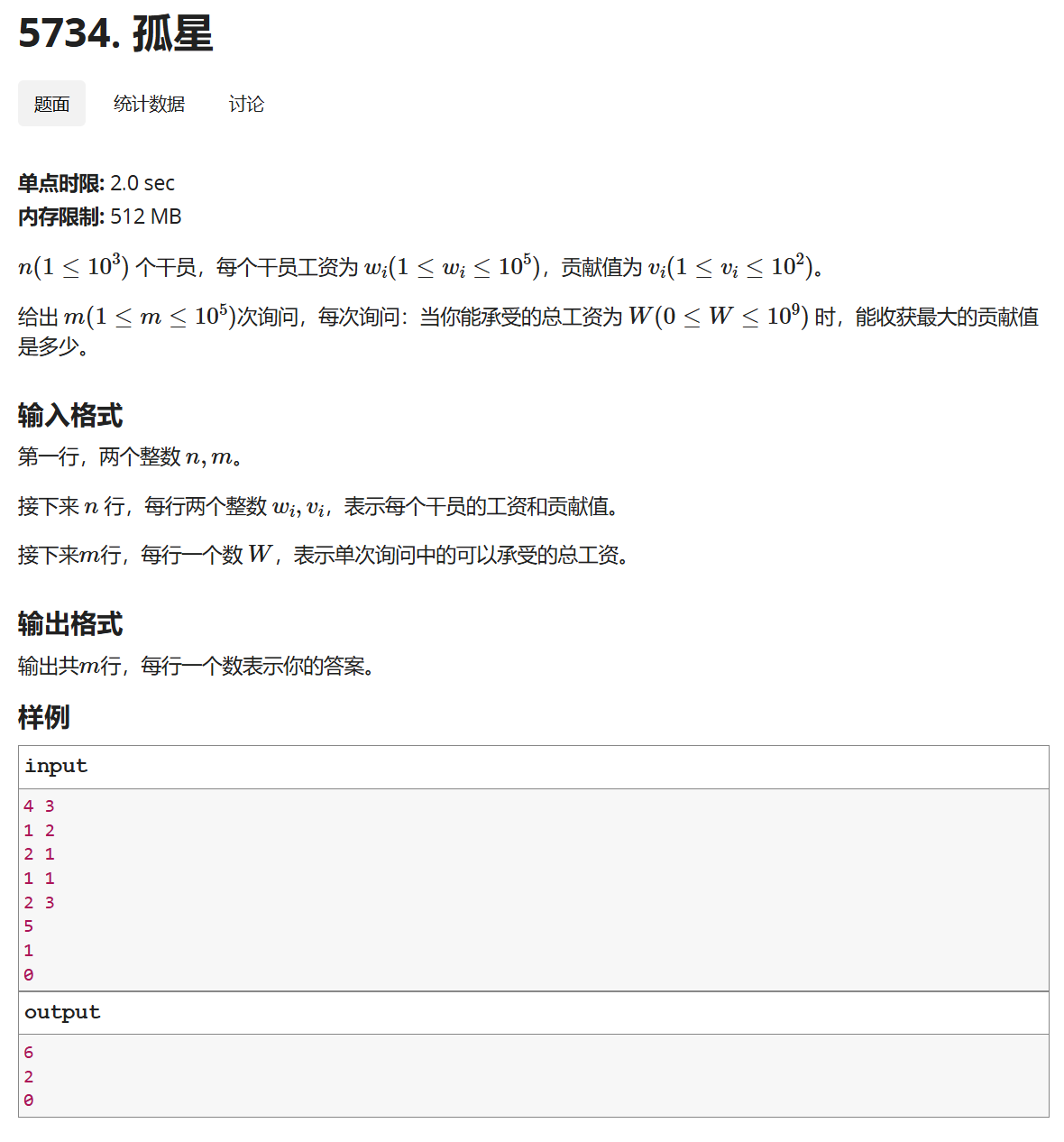
前面一篇文章给了正常小数据的做法,利用01背包的思想,贡献值就是价值(<100),重量就是工资(<100000)
//#include<stdio.h>
//int main() {
// int m, n;
// scanf("%d %d", &m, &n);
// int ganyuan[100][100];
// int q[100];//处理输入
// for (int i = 0; i < m; i++)
// {
// scanf("%d %d", &ganyuan[1+i][0],&ganyuan[1+i][1]);
// }
// for (int i = 0; i < n; i++)
// {
// scanf("%d", &q[i]);
// }// int dp[100][100];//二维dp部分
// for (int i = 0; i < 10; i++)
// {
// dp[0][i] = 0;
// }
// for (int i = 1; i <= m; i++)
// {
// for (int j = 0; j < 10; j++)
// {
// if (ganyuan[i][0] > j) {
// dp[i][j] = dp[i - 1][j];
// }
// else
// {
// if (dp[i-1][j- ganyuan[i][0]]+ ganyuan[i][1] > dp[i - 1][j])
// {
// dp[i][j] = dp[i - 1][j - ganyuan[i][0]] + ganyuan[i][1];
// }
// else
// {
// dp[i][j] = dp[i - 1][j];
// }
// }
// }
// }
// for (int i = 0; i < n; i++)
// {
// printf("%d ", dp[m][q[i]]);
// }
// /*for (int i = 1; i <= m; i++)
// {
// for (int j = 0; j < 10; j++)
// {
// printf("%d ", dp[i][j]);
// }
// printf("\n");
// }*/
// return 0;
//}但是显然数据大起来之后,二维dp非常耗空间,所以我第二个想法是转换变成一维数组,因为二维dp每一次更新一层数据都只和上一层的有关,意味着前面的数据都没有用了,
那么如果:
1.这个干员的工资比我给的工资还多就直接不要,继承上一次的值(不用动)
2.如果我要这个干员,但是这个干员会挤掉更有“性价比”的干员,那也不如继承
dp[j] > dp[j - ganyuan[i][0]] + ganyuan[i][1]
dp[j]=dp[j](不用写,因为直接继承)3.要这个干员可以在有限的工资内提高贡献值,那就要
dp[j] < dp[j - ganyuan[i][0]] + ganyuan[i][1]
dp[j]=dp[j - ganyuan[i][0]] + ganyuan[i][1]于是就有了下面的代码
for (int i = 1; i <= m; i++)
{for (int j = 0; j <= max; j++) {if (dp[j] < dp[j - ganyuan[i][0]] + ganyuan[i][1]){dp[j] = dp[j - ganyuan[i][0]] + ganyuan[i][1];}}
}但是很明显的,从前往后会修改一部分数据,导致后面用的是前面已经修改过的数据
比如干员3,工资3时,贡献值最大是3,会在算干员4时,更新成5,但是干员4在工资是5时需要用前面原有的数据而不是覆盖过的数据
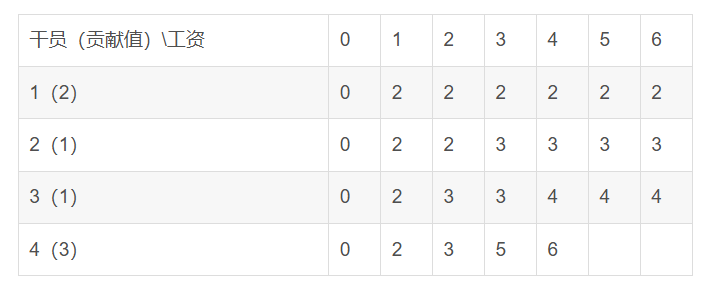
于是我就从后往前,这样就避免了数据覆盖问题
for (int i = 1; i <= m; i++)
{for (int j = max; j >= ganyuan[i][0]; j--) {if (dp[j] < dp[j - ganyuan[i][0]] + ganyuan[i][1]){dp[j] = dp[j - ganyuan[i][0]] + ganyuan[i][1];}}
}这时候又有问题了,我把内存优化了但是时间仍然超时,因为该做的循环不会少
所以这条路走不通,因为数据实在是太大了,必须换一种方法
注意到贡献值这一块其实并不大,100*1000也才100000,远远小于工资上限
题目要求的是计算工资为xx时的最大贡献值,那么假如我知道了某一个贡献值下的最低工资,那就是说明如果我低于这个工资就不能获得这么多贡献值
举个例子
正常情况下,我们根据工资来查贡献值,由于工资跨度非常大,而贡献值跨度很小,那么可能很多个工资才对应一个贡献值,可能就会出现下面这种情况,我们根据工资可以直接找对应贡献值
| 工资 | 10001 | 10002 | 10003 | 10004 |
| 贡献值 | 500 | 500 | 500 | 501 |
但是现在我们反过来,根据贡献值找这个贡献值下的最低工资,这时可能就会出现这种情况
| 贡献值 | 500 | 501 | 502 | 503 |
| 工资 | 10001 | 10004 | 10007 | 10009 |
那我要找一个工资对应的最大贡献值,只需要反向对应就行,比如工资我给10005,要找这个工资下的最大贡献值
显然这个值在10004-10007之间,501贡献值至少需要10004工资,
10005肯定够给10004工资,所以贡献值至少是501,
502至少需要10007工资,注意这里是至少,意思是达到10007才有502贡献值,
那么10005不够,说明10005工资得不到502贡献值,那么最大贡献值只能是501
理论成立开始实践
先处理输入和初始化问题,最大贡献值是100*1000=100000
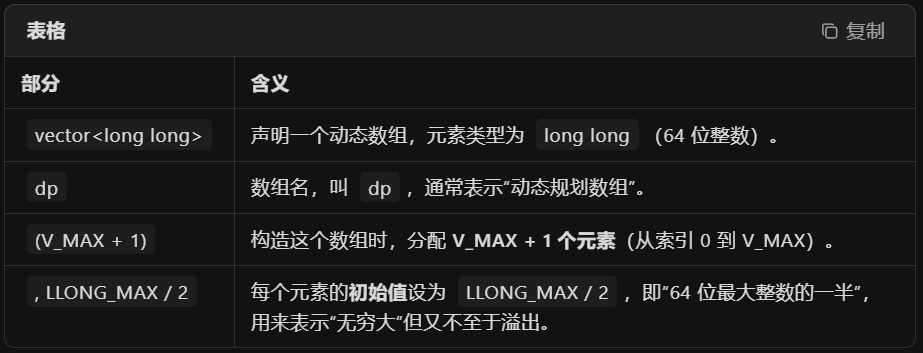
int n, m;cin >> n >> m;const int V_MAX = 100000; // 最大贡献值vector<long long> dp(V_MAX + 1, LLONG_MAX / 2); // 初始化dp数组,防止溢出dp[0] = 0;然后就是对dp的优化,保持使用前面的一维数组,这里只是做一下交换,前面是把工资看成重量,把贡献看成价值,现在要反一下,
| 维度 | 旧代码 | 新代码(第二段 C++) |
| 问题模型 | 根据工资来找贡献值 | 计算贡献值对应的最低工资要求,再看给定工资在哪个位置推最大贡献值 |
| DP 含义 | dp[j]:花费恰好 j 元时,能得到的最大贡献 | dp[j]:获得恰好 j 点贡献时,需要的最小工资 |
| DP 初值 | dp[0]=0,其余为 0(贡献值越大越好) | dp[0]=0,其余为 LLONG_MAX/2(工资越小越好) |
| 查询方式 | 直接输出 dp[W] | 预处理 g[j](≥j 的最小工资),再找最大 j 使得 g[j]≤W |
| 正确性 | 超时 | 正确 |
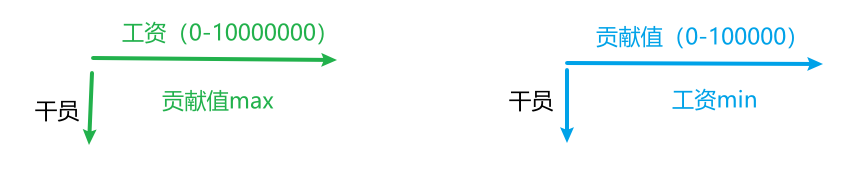
// 读取干员数据并更新dp数组for (int i = 0; i < n; i++) {int w, v;cin >> w >> v;for (int j = V_MAX; j >= v; j--) {if (dp[j - v] != LLONG_MAX / 2) { // 确保不会溢出dp[j] = min(dp[j], dp[j - v] + w);}}}备注:这里还有一个优化,前面是先输入再dp循环,但是麻烦了。实际上可以一边输入一边循环,因为循环和后面的干员无关,这样写更加简洁高效
做出贡献值和最低工资对应表后,就是下一步——查找
在数据结构里面我们学习过当数据较大时,从前往后遍历查找效率非常低,况且还要找10w个数据
因此这里就可以用二分查找找到数据所在的区间,但是二分查找有一个前提,就是数据必须是有序的,原来dp数组的数据不一定有序因为dp只是说明了在给定贡献值的情况下的最低工资,可能存在贡献值多最低工资反而更低的情况
比如有一个干员工资是1,贡献值是2;另一个工资是2,贡献值是1
那么贡献值是1时,最低工资是2;贡献值是2时,最低工资是1
因此需要做一个排序
// 预处理g数组:g[j]表示获得至少j贡献值所需的最小工资vector<long long> g(V_MAX + 1);g[V_MAX] = dp[V_MAX];for (int j = V_MAX - 1; j >= 0; j--) {g[j] = min(dp[j], g[j + 1]);}
这个排序也比较巧妙,从后往前排序,这样就不会出现贡献值多工资反而低的情况了
比如前面的例子:贡献值是1时,最低工资是2;贡献值是2时,最低工资是1
排序后贡献值是1,最低工资也是1,表示获得至少1贡献值所需的最小工资是1
对于后面的二分查找,写法不止一种,下面是可行的一种
初始化边界:
low = 0:最小可能贡献值(即使不选任何干员,贡献值也是0)high = total_value:最大可能贡献值(所有干员贡献值之和)ans = 0:初始化为最小可能值(至少可以取0)
循环条件
low <= high:确保当搜索区间缩小到单个元素时仍能处理
当
low > high时,表示搜索区间已空,循环结束
中点计算
mid = (low + high) / 2:取当前搜索区间的中间位置
整数除法自动向下取整
条件判断
g[mid] <= W:如果成立:说明至少
mid贡献值是可行的ans = mid:记录当前可行解low = mid + 1:尝试在右半区间寻找更大的可行值
如果不成立:说明
mid贡献值不可行high = mid - 1:在左半区间继续搜索
更新逻辑:
当找到一个可行解时(
g[mid] <= W),我们不满足于当前解而是尝试
mid + 1,希望找到更大的可行贡献值这确保了最终找到的是最大的满足条件的贡

while(m--){
int low = 0, high = V_max; // 设置搜索范围 [0, total_value]
int ans = 0; // 用于记录当前找到的最大可行贡献值while (low <= high) { // 当搜索区间非空时继续int mid = (low + high) / 2; // 计算当前区间的中点if (g[mid] <= W) { // 如果中点值满足条件ans = mid; // 更新当前最大可行贡献值low = mid + 1; // 尝试在右半区间寻找更大的可行值} else { // 如果中点值不满足条件high = mid - 1; // 在左半区间继续搜索}
}cout << ans << '\n'; // 输出找到的最大可行贡献值
}总代码
#include <iostream>
#include <vector>
#include <algorithm>
#include <climits>
using namespace std;int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int n, m;cin >> n >> m;const int V_MAX = 100000; // 最大贡献值vector<long long> dp(V_MAX + 1, LLONG_MAX / 2); // 初始化dp数组,防止溢出dp[0] = 0;// 读取干员数据并更新dp数组for (int i = 0; i < n; i++) {int w, v;cin >> w >> v;for (int j = V_MAX; j >= v; j--) {if (dp[j - v] != LLONG_MAX / 2) { // 确保不会溢出dp[j] = min(dp[j], dp[j - v] + w);}}}// 预处理g数组:g[j]表示获得至少j贡献值所需的最小工资vector<long long> g(V_MAX + 1);g[V_MAX] = dp[V_MAX];for (int j = V_MAX - 1; j >= 0; j--) {g[j] = min(dp[j], g[j + 1]);}while (m--) {long long W;cin >> W;int low = 0, high = V_MAX;int ans = 0;// 二分查找最大的j,使得g[j] <= Wwhile (low <= high) {int mid = (low + high) / 2;if (g[mid] <= W) {ans = mid;low = mid + 1;} else {high = mid - 1;}}cout << ans << '\n';}return 0;
}//感觉脑子快炸了 :(
