查找文献
题目描述
小 K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个(也有可能没有)参考文献的链接指向别的博客文章。小 K 求知欲旺盛,如果他看了某篇文章,那么他一定会去看这篇文章的参考文献(如果他之前已经看过这篇参考文献的话就不用再看它了)。
假设洛谷博客里面一共有 n(n≤105)n(n≤105) 篇文章(编号为 1 到 nn)以及 m(m≤106)m(m≤106) 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章,请帮助小 K 设计一种方法,使小 K 可以不重复、不遗漏的看完所有他能看到的文章。
这边是已经整理好的参考文献关系图,其中,文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。
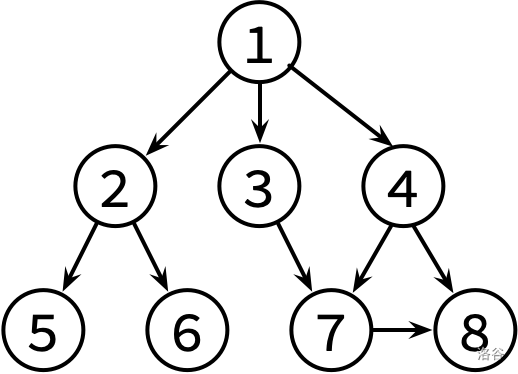
请对这个图分别进行 DFS 和 BFS,并输出遍历结果。如果有很多篇文章可以参阅,请先看编号较小的那篇(因此你可能需要先排序)。
输入格式
共 m+1m+1 行,第 1 行为 2 个数,nn 和 mm,分别表示一共有 n(n≤105)n(n≤105) 篇文章(编号为 1 到 nn)以及m(m≤106)m(m≤106) 条参考文献引用关系。
接下来 mm 行,每行有两个整数 X,YX,Y 表示文章 X 有参考文献 Y。
输出格式
共 2 行。 第一行为 DFS 遍历结果,第二行为 BFS 遍历结果。
输入数据 1
8 9
1 2
1 3
1 4
2 5
2 6
3 7
4 7
4 8
7 8
输出数据 1
1 2 5 6 3 7 8 4
1 2 3 4 5 6 7 8
这道题是典型的图遍历问题,需要我们对有向图分别两种经典遍历:深度优先搜索 (DFS) 和广度优先搜索 (BFS)。下面我将分步骤详细讲解解题思路和完整的 C++ 实现代码。
问题分析
- 有 n 篇文章 (节点) 和 m 条引用关系 (有向边)
- 从文章 1 开始,需要访问所有可达的文章
- 当有多个可选文章时,优先访问编号小的
- 分别输出 DFS 和 BFS 的遍历结果
解决方案步骤
步骤 1:数据结构选择
- 使用邻接表存储图结构:适合表示稀疏图,效率高
- 使用布尔数组标记节点是否已访问
步骤 2:输入处理与图构建
- 读取 n 和 m
- 读取 m 条边,构建邻接表
- 对每个节点的邻接列表排序,确保按编号升序访问
步骤 3:实现 DFS 算法
- 递归实现:访问当前节点→标记已访问→递归访问所有未访问的邻居
步骤 4:实现 BFS 算法
- 使用队列实现:将节点入队→出队访问→将所有未访问的邻居入队
步骤 5:输出结果
- 先输出 DFS 结果,再输出 BFS 结果
完整 C++ 代码实现
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;// 定义最大节点数,根据题目约束n≤105
const int MAXN = 100005;// 邻接表:adj[x]存储x的所有引用文献(邻居节点)
vector<int> adj[MAXN];
// 访问标记数组:记录节点是否已被访问
bool visited[MAXN];// 深度优先搜索实现
void dfs(int u) {// 标记当前节点为已访问visited[u] = true;// 输出当前节点cout << u << " ";// 遍历所有邻居节点(已排序)for (int v : adj[u]) {// 如果邻居未被访问,则递归访问if (!visited[v]) {dfs(v);}}
}// 广度优先搜索实现
void bfs(int start) {// 创建队列并将起始节点入队queue<int> q;q.push(start);// 标记起始节点为已访问visited[start] = true;// 队列非空时循环while (!q.empty()) {// 取出队首节点int u = q.front();q.pop();// 输出当前节点cout << u << " ";// 遍历所有邻居节点for (int v : adj[u]) {// 如果邻居未被访问if (!visited[v]) {// 标记为已访问并加入队列visited[v] = true;q.push(v);}}}
}int main() {// 读取节点数n和边数mint n, m;cin >> n >> m;// 读取m条边,构建邻接表for (int i = 0; i < m; i++) {int x, y;cin >> x >> y;// 添加有向边x->yadj[x].push_back(y);}// 对每个节点的邻居列表进行排序// 确保在有多个选择时,优先访问编号小的节点for (int i = 1; i <= n; i++) {sort(adj[i].begin(), adj[i].end());}// 执行DFS并输出结果// 先重置访问标记数组fill(visited, visited + n + 1, false);dfs(1);cout << endl;// 执行BFS并输出结果// 再次重置访问标记数组fill(visited, visited + n + 1, false);bfs(1);cout << endl;return 0;
}
代码分步讲解
数据结构定义
const int MAXN = 100005; vector<int> adj[MAXN]; // 邻接表存储图 bool visited[MAXN]; // 访问标记数组- MAXN 定义了最大节点数,满足题目 n≤105 的要求
- adj 是邻接表,adj [x] 存储所有被 x 引用的文献
- visited 数组标记标记节点是否已访问
DFS 实现
void dfs(int u) {visited[u] = true; // 标记当前节点为已访问cout << u << " "; // 输出当前节点for (int v : adj[u]) { // 遍历所有邻居if (!visited[v]) { // 若邻居未访问dfs(v); // 递归访问}} }- 递归思想:先访问当前节点,再深入访问每个未访问的邻居
- 由于邻居列表已排序,保证了按编号升序访问
BFS 实现
void bfs(int start) {queue<int> q;q.push(start); // 起始点入队visited[start] = true; // 标记为已访问while (!q.empty()) {int u = q.front(); // 取出队首q.pop();cout << u << " "; // 输出for (int v : adj[u]) {if (!visited[v]) {visited[v] = true;q.push(v); // 未访问的邻居入队}}} }- 队列思想:按层次访问,先访问完当前层再进入下一层
- 同样利用已排序的邻居列表保证访问顺序
主函数流程
int main() {// 1. 读取输入cin >> n >> m;for (int i = 0; i < m; i++) {int x, y;cin >> x >> y;adj[x].push_back(y);}// 2. 排序邻居列表for (int i = 1; i <= n; i++) {sort(adj[i].begin(), adj[i].end());}// 3. 执行DFSfill(visited, visited + n + 1, false);dfs(1);cout << endl;// 4. 执行BFSfill(visited, visited + n + 1, false);bfs(1);cout << endl;return 0; }- 读取输入并构建邻接表
- 关键步骤:对每个节点的邻居排序,确保按编号升序访问
- 分别执行 DFS 和 BFS,每次执行前重置 visited 数组
通过这个实现,我们完美解决了问题要求:从文章 1 开始,不重复不遗漏地访问所有可达文章,并按编号升序选择下一篇文章,分别输出 DFS 和 BFS 的遍历结果。
