一维dp-序列类型-最长有效括号

最长有效括号

Solution

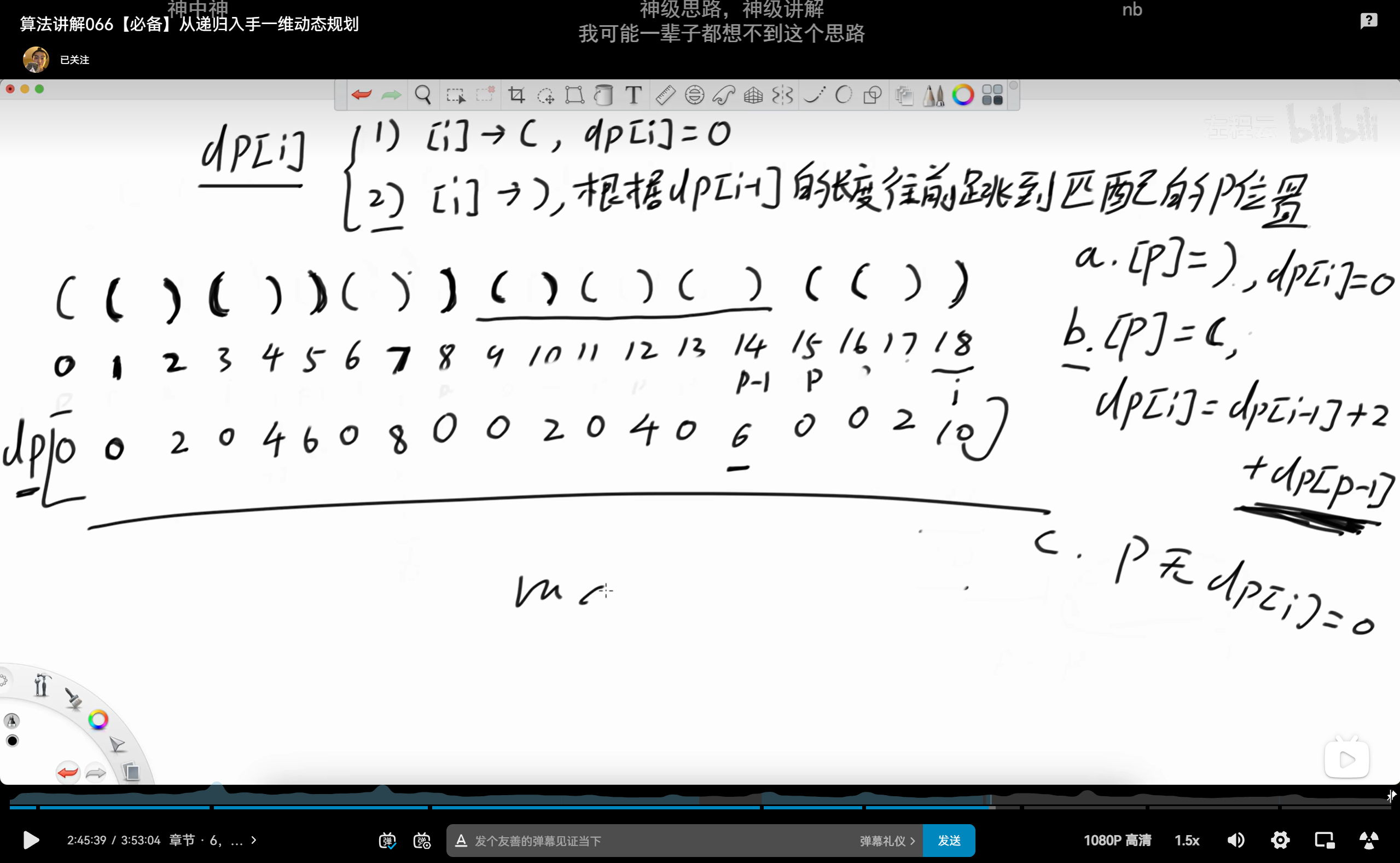
这题的难点在于状态转移方程，由于这里是一维序列，所以很容易想到用“以第i个字符结尾的…”来定义状态，关键就在于寻找后面的状态是怎样依赖于前面的状态。

#include<iostream>
#include<vector>
using namespace std;int longestValidParentheses(string s) {int n = s.length();vector<int> dp(n + 1, 0);int ans = 0;//dp(i）表示以第i个字符结尾的最大有效括号长度for (int i = 1; i < n; ++i) {//以左括号结尾的一定等于0if (s[i] == '(') continue;//以右括号结尾else {//寻找与该括号匹配的左括号int p = i - dp[i - 1] - 1;if (p >= 0 && s[p] == '(') {dp[i] = dp[i - 1] + 2;//找到匹配的左括号了，先长度加二，还需要继续分析//因为就算这里匹配上了，还要考虑再上一个位置if (p - 1 >= 0) dp[i] += dp[p - 1];}ans = max(ans, dp[i]);}}return ans;
}
int main() {string s;cin >> s;cout << longestValidParentheses(s);return 0;
}