算法篇----位运算
一、常见题型总结
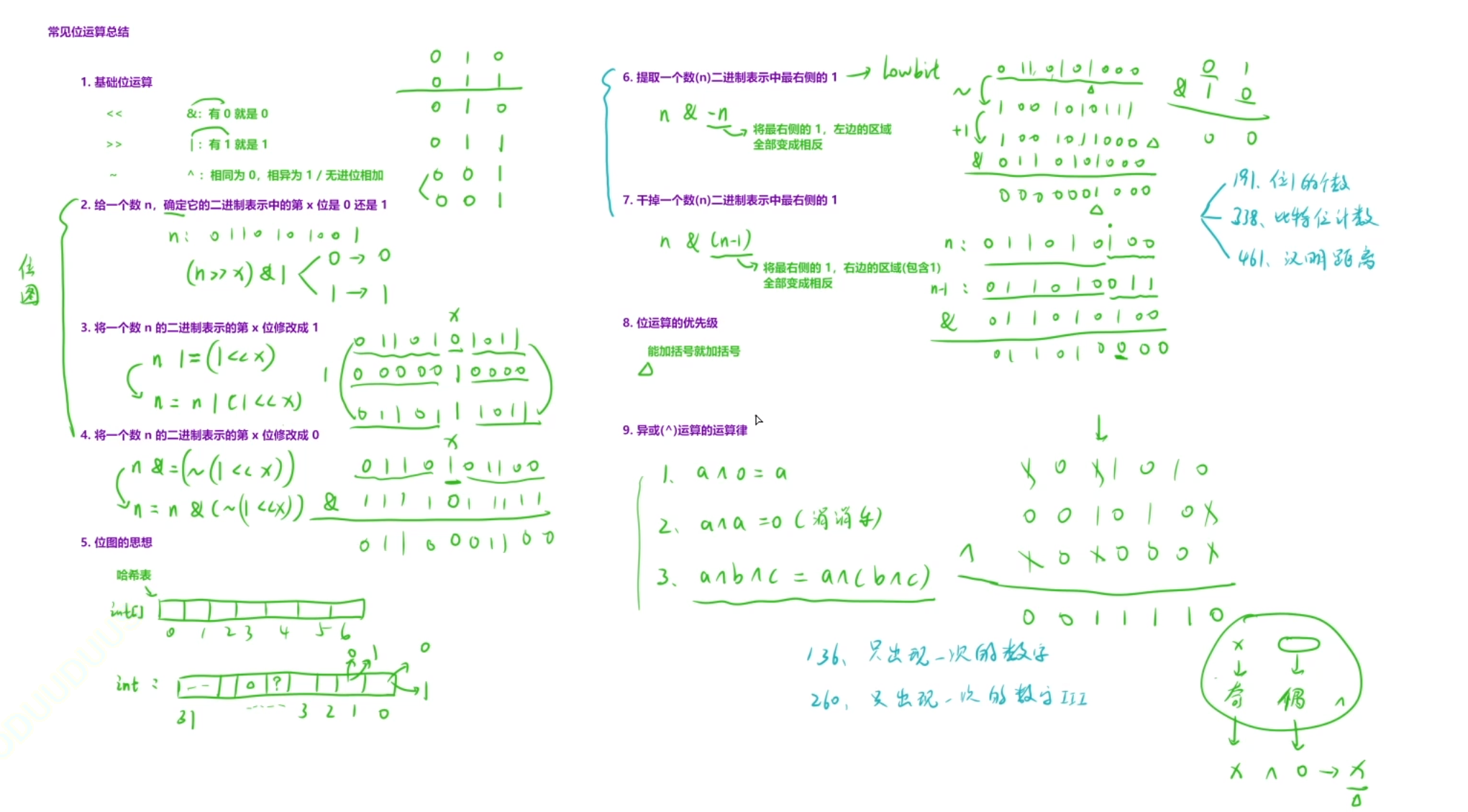
1.基础位运算
<< 左移
>> 右移
~ 取反
& 与(有0为0)
| 或(有1为1)
^ 异或(相同为0,相异为1)(无进位相加)
2.给一个数n,确定它的二进制表示中的第x位是0还是1
说明:最右边是第0位,从右到左以此类推!
解决方法:利用&的性质
(n>>x)&1
3.将一个数n的二进制表示的第x位修改为1
解决方法:利用|的性质
n |= (1<<x) 即n=n|(1<<x)
4.将一个数n的二进制表示的第x位修改为0
解决方法:利用&的性质
n&=(~(1<<x)) 即n=n&(~(1<<x))
5.位图的思想
我们在之前曾用过数组来模拟哈希表,这里我们可以将位图简单理解为二进制数组,每一位都存的是0和1,那我们在修改某一位时就会用到前面总结的几点!
下图为数组构成的哈希表与位图之间的区别~
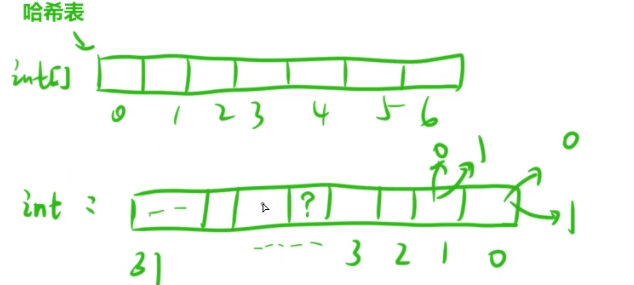
6.提取一个数(n)二进制表示中最右侧的1
解决方法:lowbit操作,即n & -n ,-n:将最右侧的1,左边的区域,全部变成相反,如下图示例:
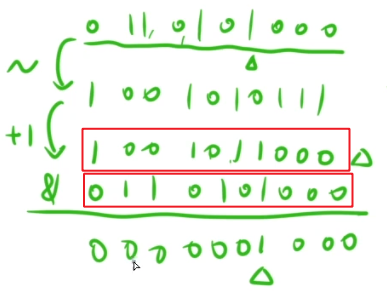
这样,n&-n就可以把最右侧的1提取到!
7.干掉一个数(n)二进制表示中最右侧的1
解决方法:n & (n-1) ,n-1表示为将最右侧的1,右边的区域(包含1)全部变成相反,图片示例:

8.位运算的优先级
能加括号就加括号
9.异或(^)运算的运算律
a^a=0
a^0=a
a^b^c=a^(b^c) 用无进位加法可以验证~
最后,总结:
二、实战应用
1.判断字符是否唯一
面试题 01.01. 判定字符是否唯一 - 力扣(LeetCode)
解题思路:
这道题目解题思路非常多样,这里都简单说一下~
方法一)暴力破解
就是在硬造一个数组,每次往这个数组里面填字符时,都比对一下是否与前文冲突,时间复杂度为O(N^2),代码看看就行了,没啥技术含量!!!
class Solution {
public:bool isUnique(string astr) {int len=astr.length();char arr[len+1];arr[0]=astr[0];for(int i=1;i<len;i++){arr[i]=astr[i];for(int j=0;j<i;j++){if(arr[j]==astr[i]){return false;}}i++;}return true;}
};
方法二)哈希表
就是存入哈希表之前看一下之前这个字符存过没有,存过就fasle,没存过就存一下
class Solution {
public:bool isUnique(string astr) {int hash[26]={0};for(auto e:astr){int i=e-'a';if(hash[i]==0) hash[i]++;else return false;}return true;}
};
方法三)位图
基本思想还是看之前出现过没有,只不过我们可以用位运算的操作来处理,因此用一下位图,(有31个位,但是我们只用25个就好啦~一个字符代表一个位),0表示不存在,1表示存在,公式忘了可以看看上文总结的公式!
注:这里我们可以优化一下,利用鸽巢原理,即如果字符串长度大于26,那就直接false就可以了!因为这样包重复的!!
class Solution {
public:bool isUnique(string astr) {//利用鸽巢原理简化if(astr.size()>26) return false;int bitmap=0;for(auto e:astr){int i=e-'a';//先判断是否存在if(((bitmap>>i)&1)==1) return false;//把当前字符加入到位图中,即将对应位修改为1bitmap |= (1<<i);}return true;}
};2.缺失的数字
268. 丢失的数字 - 力扣(LeetCode)
解题思路:
方法一)高斯求和
class Solution {
public:int missingNumber(vector<int>& nums) {int n=nums.size();int sum=n*(n+1)/2;for(auto e:nums){sum-=e;}return sum;}
};方法二)哈希表
class Solution {
public:int missingNumber(vector<int>& nums) {int hash[10000]={0};for(auto e:nums){hash[e]++;}int miss=1;for(int i=0;i<10000;i++){if(hash[i]==0){miss=i;break;}}return miss;}
};方法三)位图
利用异或的性质即可(a^a=0)
class Solution {
public:int missingNumber(vector<int>& nums) {int n=nums.size(),sum=0;for(auto x:nums) sum^=x;for(int i=0;i<=n;i++){sum^=i;}return sum;}
};3.两整数之和
371. 两整数之和 - 力扣(LeetCode)
解题思路:
方法一)
在笔试中,可以不讲武德,直接return a+b(老师说应该面试官不会看),但是作为练习,这样是不负责滴!
方法二)
我们可以接着借助位运算的操作,之前提到过异或(^)是无进位加法,那么我们只需找到进位即可~
恰巧按位与(&)就是进位,因为
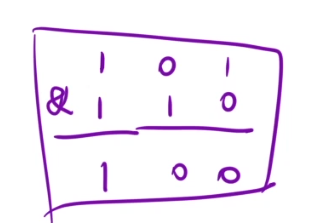
所以我们就让x=a^b就好了,在加上进位c=(a&b),但是进位是加在下一位上的,不是加在本位上的,所以我们要将进位右移一下:(a&b)<<1,之后将x和c无进位相加就好(x^c),重复上述过程,直到进位为0,问题解决!
class Solution {
public:int getSum(int a, int b) {while(b){int x=a^b;unsigned int c=(unsigned int)(a&b)<<1; //防止c为-1时,<<操作未定义a=x;b=c;}return a;}
};4.只出现一次的数字
137. 只出现一次的数字 II - 力扣(LeetCode)
解题思路:
我们先分析这样一个事情,就是这些n个数加起来会又得到一个新的数,那么把这个新的数拆开看,用位图的方式,那每一位无非就是0或者1,但是实际上是由四种方式构成的~
如下图所示:

最后结果用ret表示,位图
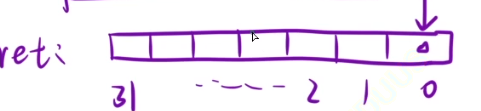
就是从右向左依次看每一位,对应的位是0就保持为0,是1就将其修改为1
class Solution {
public:int singleNumber(vector<int>& nums) {int ret=0;for(int i=0;i<32;i++) //依次去修改ret中的每一位{int sum=0;for(int x:nums) //计算Nums中所有数第i位的和if(((x>>i)&1)==1)sum++;sum%=3;if(sum==1) ret|=1<<i;}return ret;}
};
