小杰数据结构(four day)——藏器于身,待时而动。
1.队列
(1)顺序队列(循环队列)
特点:先进先出 FIFO
两个指针
front和rear
front即队头指针指向队头元素,rear即队尾指针指向队尾元素的下一个元素。这样当
front等于rear时,不是队列中有一个元素,而是表示空队列。
假溢出:
队头front前有空余空间,队尾rear已经指向空间最末尾了
解决方法:
头尾相连形成循环队列。
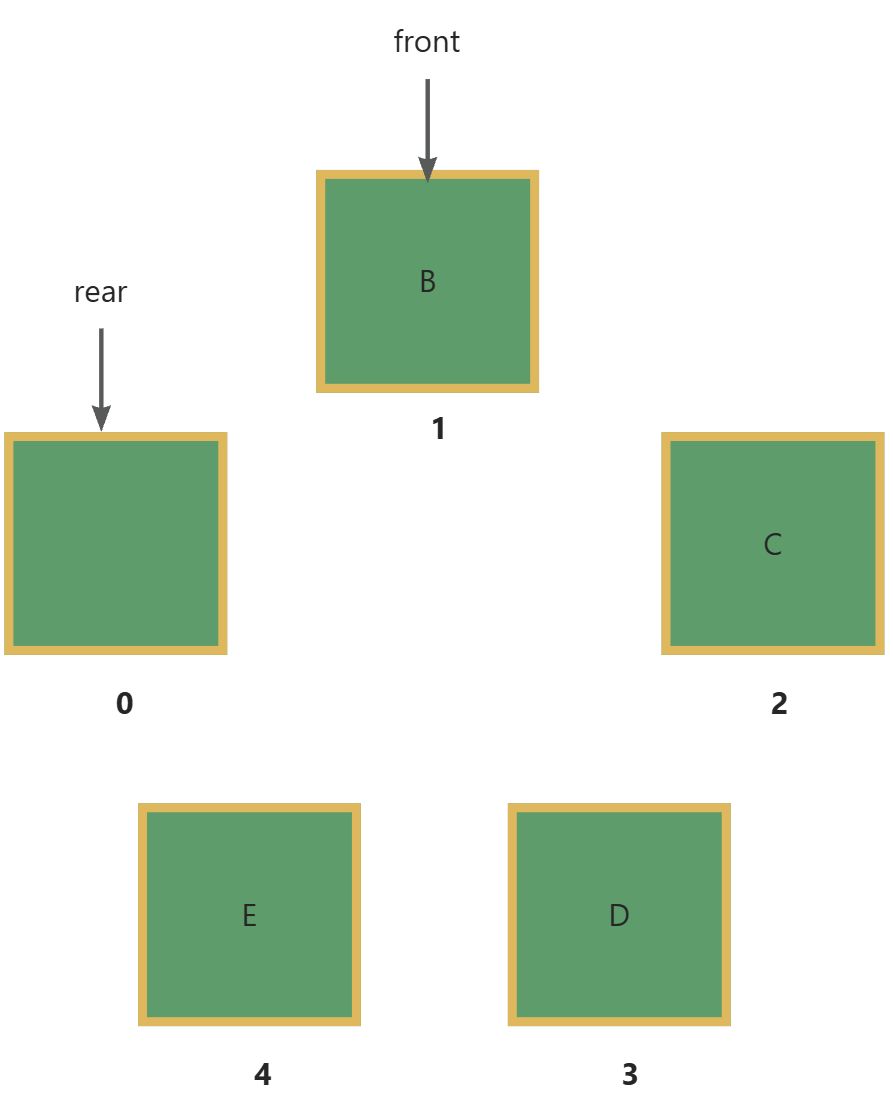
此时如果再入列一个元素,会发现rear和front重合了。重合则无法判断其是满还是空。
所以解决方法:
当队列空时,判断条件就是rear == front,当队列满时,我们修改其判断条件,保留一个元素空闲。
此时一个满队的条件是
rear加一,对循环队列长度取余后,等于front则说明其是满队。
(rear+1)%N == frontrear和front往后走的公式:
rear= (rear+1)%N
front= (front+1)%N
- 逻辑结构:线性结构
- 物理结构:顺序存储结构
整体代码:
class SeqQueue:def __init__(self, max_len=5):self.max_len = max_len # 队列的最大长度self.rear = 0 # 入队端self.front = 0 # 出队端self.data = [0] * max_len # 队列的存储空间# 2.入列 data代表入列的数据def enqueue(self, data):if self.is_full():print("enqueue error")returnself.data[self.rear] = dataself.rear = (self.rear+1) % self.max_len# 3.判断队列是否为满def is_full(self):return (self.rear+1) % self.max_len == self.front# 4.判断队列是否为空def is_empty(self):return self.front == self.rear# 5.出列def dequeue(self):if self.is_empty():print("dequeue error")returnnew = self.data[self.front]self.front = (self.front + 1) % self.max_lenreturn new# 6.求队列有效的长度def length(self):# length = 0# current = self.front# while current == self.rear:# current = (current + 1) % self.max_len# length += 1# return length# if self.rear >= self.front:# length = self.rear - self.front# else:# length = self.rear - self.front + self.max_len# return lengthlength = (self.front + self.rear) % self.max_lenreturn length# 7.清空队列函数def clear(self):return self.front == self.rearif __name__ == '__main__':seq_queue = SeqQueue()for i in range(4):seq_queue.enqueue(i)print("queue_len",seq_queue.length())for i in range(4):print("queue_data:%s" % seq_queue.dequeue())
输出:
queue_len 4
queue_data:0
queue_data:1
queue_data:2
queue_data:3Process finished with exit code 0
(2)链式队列
链式栈:无头单向链表,头为栈顶,对无头单向链表进行头插和头删。
链式队列:有头单向链表,头结点为队头,终端结点为队尾,对有头单向链表进行头删和尾插。
链式队列:
队列的链式存储结构,其实就是线性表的单链表,只能尾进头出
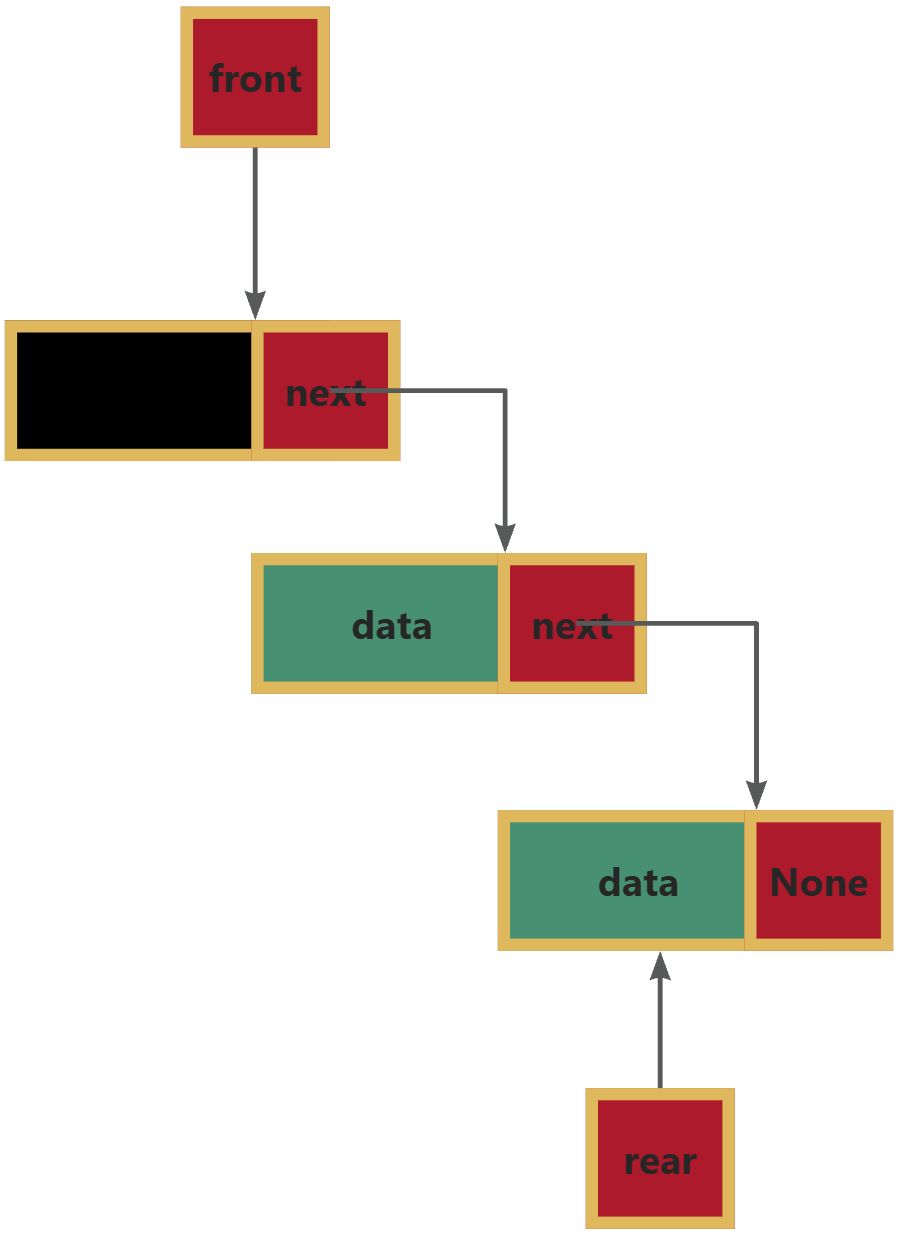
出列有两种思路方式:
1.挨个释放,直至释放到rear所指的零节点,让rear去找到front
2.头节点挨个移动并释放,直至找到rear所指的零节点,并将此零节点zuowei新的头节点
整体代码
# 1、定义链式队列节点
class Node:def __init__(self, value):self.data = value # 数据域self.next = None # 指针域# 定义队列函数
class LinkQueue:# 队列初始化def __init__(self):self.front = Node(None) # 相当于队列的头指针self.rear = self.front # 相当于队列的尾指针# 2、判断队列是否为空def is_empty(self):# return self.front == self.rearreturn self.front.next is None# 3、元素入队def inlinkqueue(self, data):new = Node(data)self.rear.next = new# self.rear = self.rear.nextself.rear = new# 4、队列元素出队def outlinkqueue(self):if self.is_empty():print("qutlinkqueue error")return# data = self.front.next.data# self.front = self.front.next# return data# data = self.front.next# self.front.next = self.front.next.next# if self.front.next is None:# self.rear = self.frontdata = self.front.nextif self.front.next == self.rear:self.rear = self.frontself.front.next = data.nextreturn data.data# 5、获取队首元素def get_top(self):if self.is_empty():return "get_top error"return self.front.next.data# 6、遍历队列def display(self):if self.is_empty():print("display error")returncurrent = self.frontwhile current.next:current = current.nextprint(current.data)# 7、清空队列def clearlinkqueue(self):# self.front = self.rearwhile not self.is_empty():self.outlinkqueue()# 8、返回队列长度def lengthlinkqueue(self):length = 0current = self.front# while current != self.rear:while current.next:length += 1current = current.nextreturn lengthif __name__ == '__main__':link_queue = LinkQueue()for i in range(6):link_queue.inlinkqueue(i)print("queue_topdata=", link_queue.get_top())print("queue_len=", link_queue.lengthlinkqueue())for _ in range(6):print("queue_data", link_queue.outlinkqueue())输出:
queue_topdata= 0
queue_len= 6
queue_data 0
queue_data 1
queue_data 2
queue_data 3
queue_data 4
queue_data 5Process finished with exit code 0
2.树
逻辑结构:层次结构
物理结构:顺序存储、链式存储
(1)概念
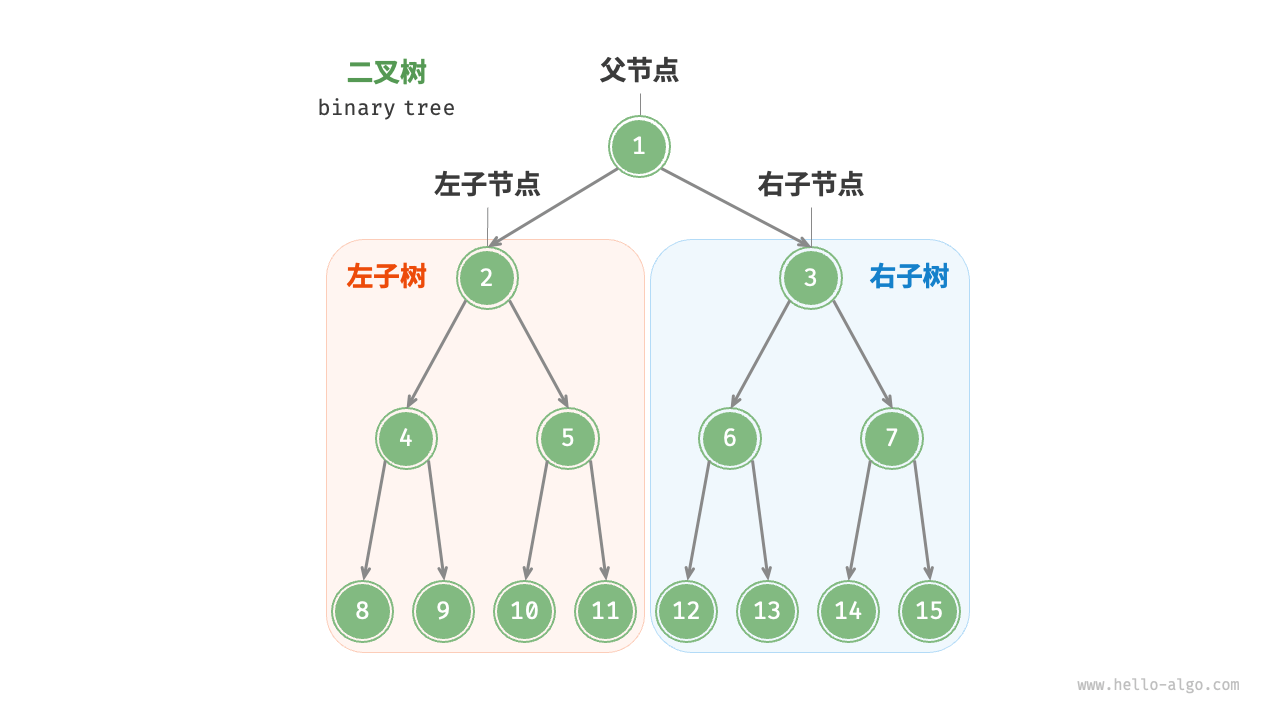
二叉树(binary tree)是一种非线性数据结构,“一分为二”的分治逻辑,基本单元是节点,每个节点包含值、左子节点引用和右子节点引用。
每个节点都有两个引用(指针),分别指向左子节点(left-child node)和右子节点(right-child node),该节点被称为这两个子节点的父节点(parent node)。当给定一个二叉树的节点时,我们将该节点的左子节点及其以下节点形成的树称为该节点的左子树(left subtree),同理可得右子树(right subtree)。
(2) 性质*
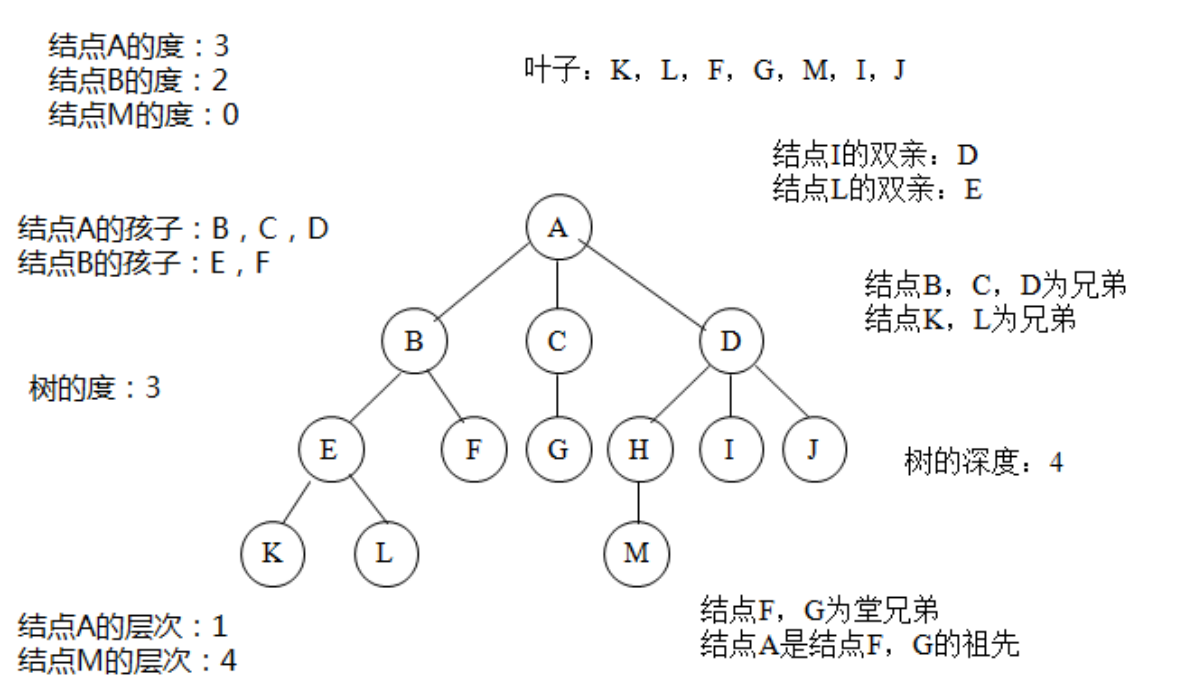
①关于树的一些基本概念
(1)度数:一个节点的子树的个数(一个节点的子树的个数称为该节点的度数,3)
(2)树度数:树中节点的最大度数,二叉树的树度数最大为2
(3)叶节点或终端节点: 度数为零的节点
(4)分支节点:度数不为零的节点(B一层)
(5)内部节点:除根节点以外的分支节点 (B,C,D)
(6)节点层次: 根节点的层次为1,根节点子树的根为第2层,以此类推
(7)树的深度或高度: 树中所有节点层次的最大值 (4)
- 二叉树的第
k层上的结点最多个2k-1个 - 深度为
k的二叉树最多有2k-1个结点 - 在任意一颗二叉树中,树叶的数目比度数为
2的结点数目多1 
满二叉树和完全二叉树
满二叉树:
深度为
k(k>=1)时,第k层结点个数为2k-1
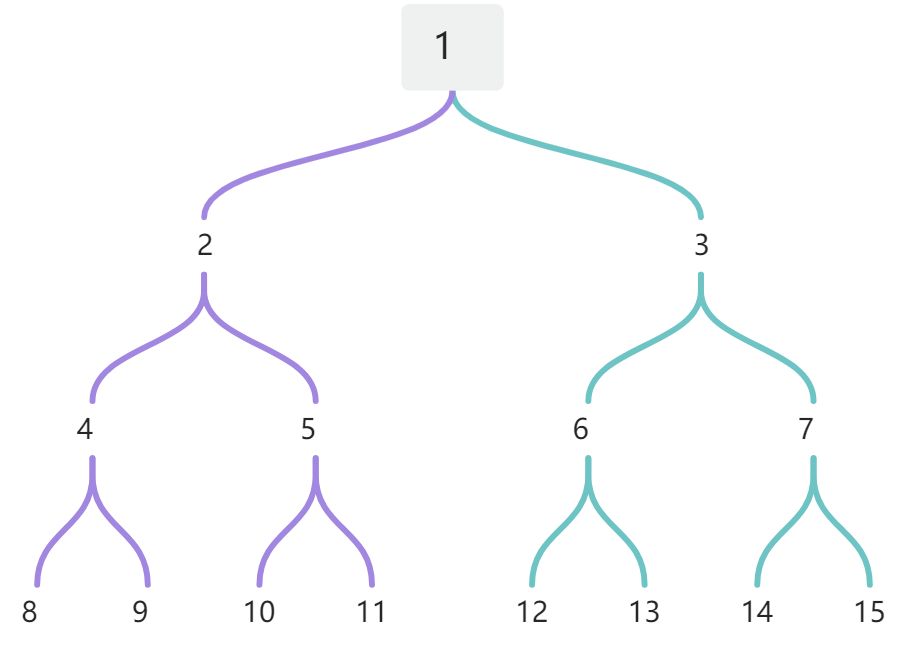
完全二叉树:
只有最下面两层有度数小于
2的节点,且最下面一层的结点集中在最左边的若干位置上。
②顺序存储
想要顺序存储普通二叉树,就需要将其提前转换成完全二叉树。
普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些结点,将其"拼凑"成一个完全二叉树即可。
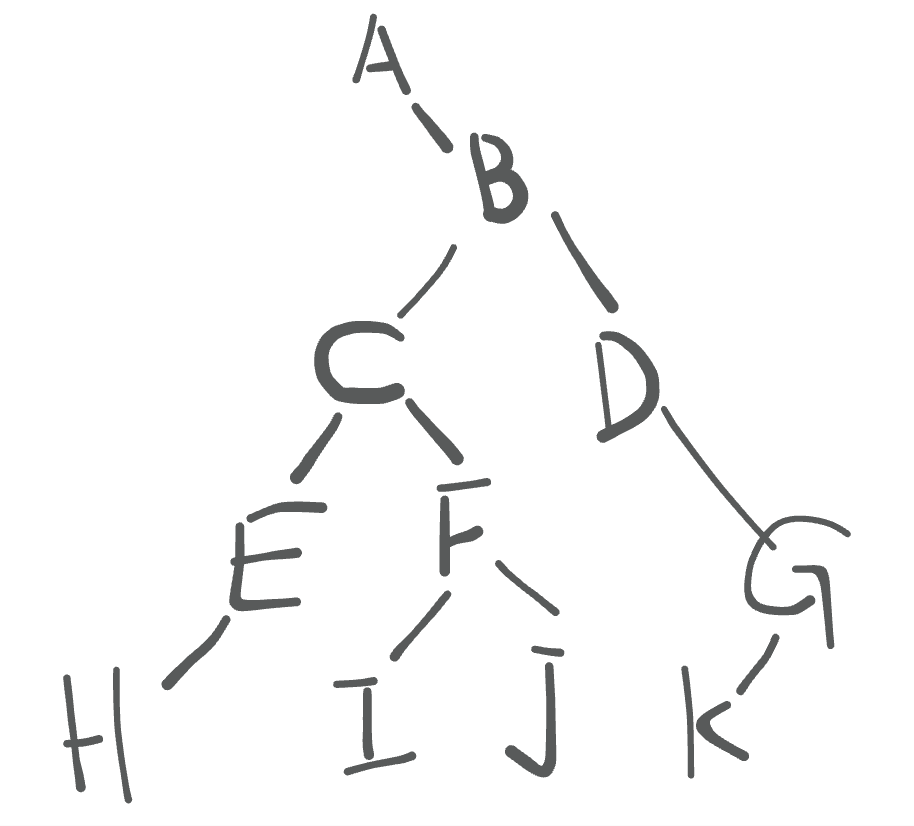
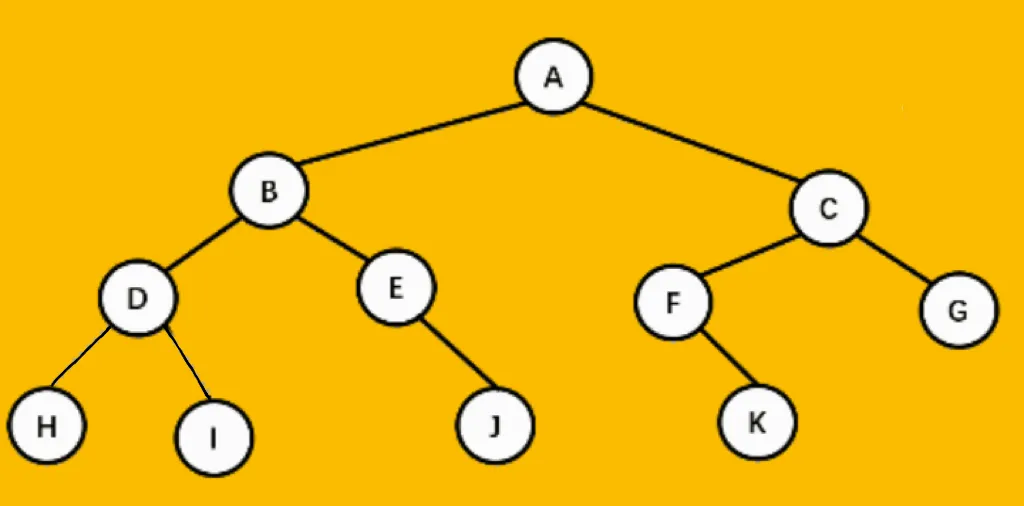
如图所示:
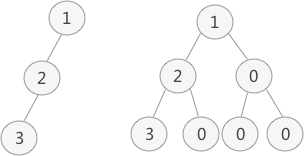
左侧是普通二叉树,右侧是转化后的完全(满)二叉树。
全(满)二叉树的顺序存储,仅需要从根结点开始,按照层次依次将树中结点存储到数组即可。
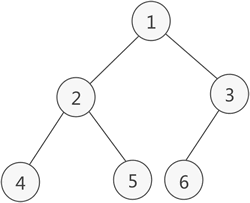
存储图 2 所示的完全二叉树:

储由普通二叉树转化来的完全二叉树也是如此。
图 1 中普通二叉树在顺组中的存储状态如图:

③ 树的遍历方式
前序遍历(先序):根左右
中序遍历:左根右
后序遍历:左右根
先序:根----->左----->右
ABDHIEJCFKG
中序:左----->根----->右
HDIBEJAFKCG
后序:左----->右----->根
HIDJEBKFGCA
练习:
已知遍历结果如下,试画出对应的二叉树,写出后序:
先序:
A B C E H F I J D G K根----->左----->右中序:
A H E C I F J B D K G左----->根----->右确定唯一一颗二叉树:
先、中
中、后
两种方式:中序为主法和先序或后序为主,然后进行二分法