【计算机组成原理】第二章：数据的表示和运算（上）

本篇笔记课程来源：王道计算机考研 计算机组成原理

接下节：【计算机组成原理】第二章：数据的表示和运算（下）

一、进位计数制

1. 进制计数法

• 基数：每个数码位所用到的不同符合的个数。
  • $R$ 进制的基数是 $R$
• 位权：指的是数制中每个数位所对应的 “权重”，它与该数位的位置相关。
  • 对于基数为 R 的数制，小数点左边第 $n$ 位（从 0 开始计数）的位权为 $R^n$，小数点右边第 $m$ 位的位权为 $R^{-m}$
• 对于 $R$ 进制：基数 = $R$，每个数码位可能出现 $R$ 种字符，逢 $R$ 进 $1$
• 计算机使用二进制的原因：
  1. 可使用两个稳定状态的物理器件表示
  2. 0，1 正好对应逻辑假、真。方便实现逻辑运算
  3. 可以很方便地使用逻辑电路实现算术运算

2. 其他进制转十进制

• $R$ 进制数的数值 = 各数码位与位权的乘积之和，即（$R$ 进制转十进制公式）： $$\begin{array}{rl}& K_n{K}_{n-1}\dots K_0{K}_{-1}\dots K_{-m}\\ & =K_n\times R^n+K_{n-1}\times R^{n-1}+\cdots +K_0\times R^0+\\ & K_{-1}\times R^{-1}+\cdots +K_{-m}\times R^{-m}\end{array}$$
• 二进制转十进制：$$\begin{array}{rl}& (10010010.110{)}_2\\ & =1\times 2^7+0\times 2^6+0\times 2^5+1\times 2^4+0\times 2^3+0\times 2^2+1\times 2^1+0\times 2^0+1\times 2^{-1}+1\times 2^{-2}+0\times 2^{-3}\\ & =128+0+0+16+0+0+2+0+0.5+0.25+0\\ & =(146.75{)}_{10}\end{array}$$
• 八进制转十进制：
  $$\begin{array}{rl}(345.6{)}_8& =3\times 8^2+4\times 8^1+5\times 8^0+6\times 8^{-1}\\ & =192+32+5+0.75\\ & =(229.75{)}_{10}\end{array}$$
• 十六进制转十进制：
  $$\begin{array}{rl}(1A3.F{)}_{16}& =1\times 16^2+A\times 16^1+3\times 16^0+F\times 16^{-1}\\ & =256+160+3+0.9375\\ & =(419.9375{)}_{10}\end{array}$$

3. 二、八、十六进制互转

• 二进制转八进制：3 位一组，每组转换成对应的八进制符号
• 二进制转十六进制：4 位一组，每组转换成对应的十六进制符号
• 八进制转二进制：每位八进制对应 3 位二进制
• 十六进制转二进制：每位十六进制对应 4 位二进制
• 对于八、十六进制转二进制凑不够的位数进行补位：
  • 整数部分高位补 0
  • 小数部分低位补 0

十进制（Decimal, D）	二进制（Binary, B）	八进制（Octal, O）	十六进制（Hexadecimal, H）
0	0000	0	0
1	0001	1	1
2	0010	2	2
3	0011	3	3
4	0100	4	4
5	0101	5	5
6	0110	6	6
7	0111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

4. 十进制转其他进制

• 整数部分：除基取余法，先取得的 “余” 是整数的低位

• 小数部分：乘基取整法，先得到的 “整” 是小数的高位。有的小数无法用二进制精确表示

  将十进制数 $158.5$ 转换为二进制：

  • 整数部分采用 除基取余法（这里的基数是 2），倒序排列余数：$$\begin{array}{rl}158÷2& =79\text{余}0(a_0=0)\\ 79÷2& =39\text{余}1(a_1=1)\\ 39÷2& =19\text{余}1(a_2=1)\\ 19÷2& =9\text{余}1(a_3=1)\\ 9÷2& =4\text{余}1(a_4=1)\\ 4÷2& =2\text{余}0(a_5=0)\\ 2÷2& =1\text{余}0(a_6=0)\\ 1÷2& =0\text{余}1(a_7=1)\end{array}$$
    倒序排列余数得：$(158{)}_{10}=(10011110{)}_2$
  • 小数部分采用 乘基取整法，顺序排列整数部分：$$\begin{array}{rl}0.5\times 2& =1.0\lfloor 1.0\rfloor =1(b_{-1}=1)\\ 0.0\times 2& =0.0\lfloor 0.0\rfloor =0(\text{终止})\end{array}$$
    顺序排列整数得：$(0.5{)}_{10}=(0.1{)}_2$
  • 将整数部分与小数部分合并：$(158.5{)}_{10}=(10011110.1{)}_2$

• 十进制转二进制也可以用拼凑法

  指数（$2^n$）	值	指数（$2^n$）	值
  $2^{-3}$	0.125	$2^5$	32
  $2^{-2}$	0.25	$2^6$	64
  $2^{-1}$	0.5	$2^7$	128
  $2^0$	1	$2^8$	256
  $2^1$	2	$2^9$	512
  $2^2$	4	$2^{10}$	1024
  $2^3$	8	$2^{11}$	2048
  $2^4$	16	$2^{12}$	4096

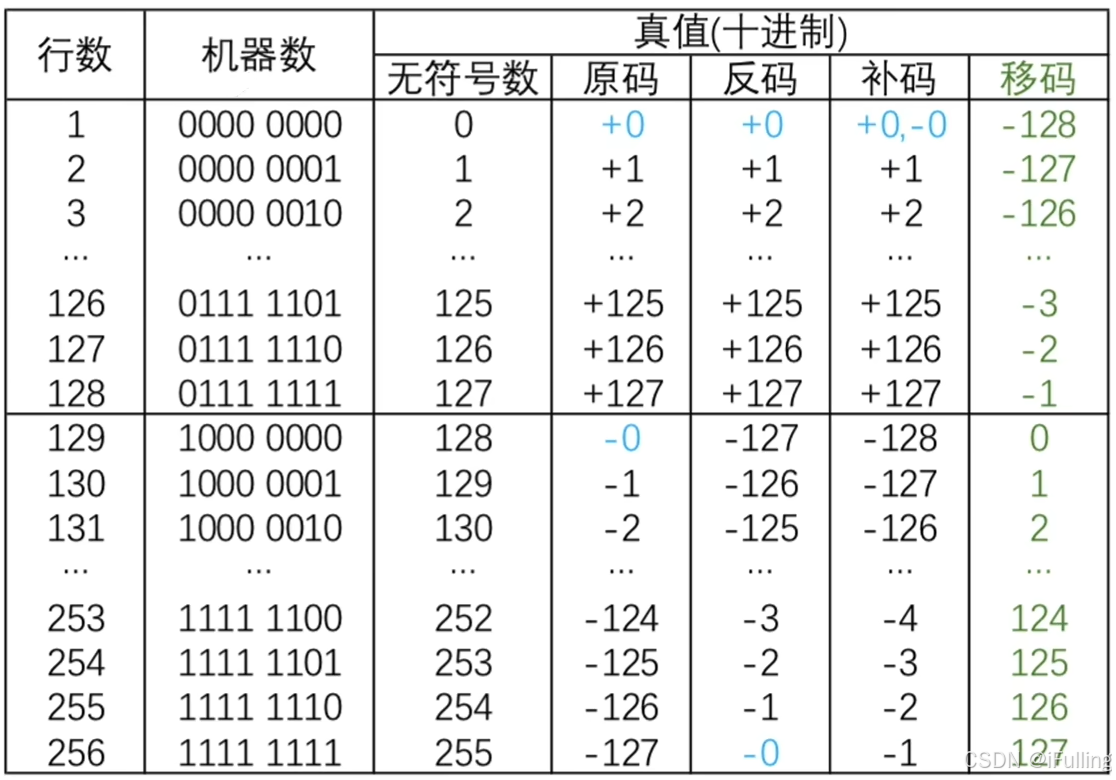
5. 真值和机器数

• 真值：符合人类习惯的数字
• 机器数：数字实际存到机器里的形式，正负号需要被 “数字化”（0、1 表示）

  真值（十进制）	机器数（8位二进制补码）
  +15	00001111
  -8	11111000

二、定点数的编码表示

• 定点数：小数点的位置固定不变（$996.007$）
• 浮点数：小数点的位置不固定（$9.96007\times 10^2$）
• 定点数的表示：
  • 无符号数：整个机器字长的全部二进制位均为数值位，没有符号位，相当于数的绝对值。
  • 有符号数：原码、反码、补码、移码

1. 无符号数

• 无符号数：
  • 整个机器字长的全部二进制位均为数值位，没有符号位，相当于数的绝对值。
  • 通常只有无符号整数，没有无符号小数
• $n$ 位的无符号数表示范围：$0$ ~ $2^n-1$

  8 位二进制无符号数表示范围：$2^8-1=255$ 种

2. 有符号数

• 每个有符号数包括符号位和数值部分：
  • 符号位：0 表示正、1 表示负
  • 数值部分：也称为 “尾数”，若机器字长为 $n$ 位，则尾数占 $n-1$ 位
  • 保存一个小数需要把整数部分和小数部分单独保存
• 定点整数：小数点隐含在最低位的后面，最高位为符号位
  
• 定点小数：小数点隐含在符号位的后面，最高位为符号位
  
• 若真值为 x，可用 原码（[x]_原）、反码（[x]_反）、补码（[x]_补） 三种方式来表示定点整数和定点小数，还可以用 移码（[x]_移） 表示定点整数
  

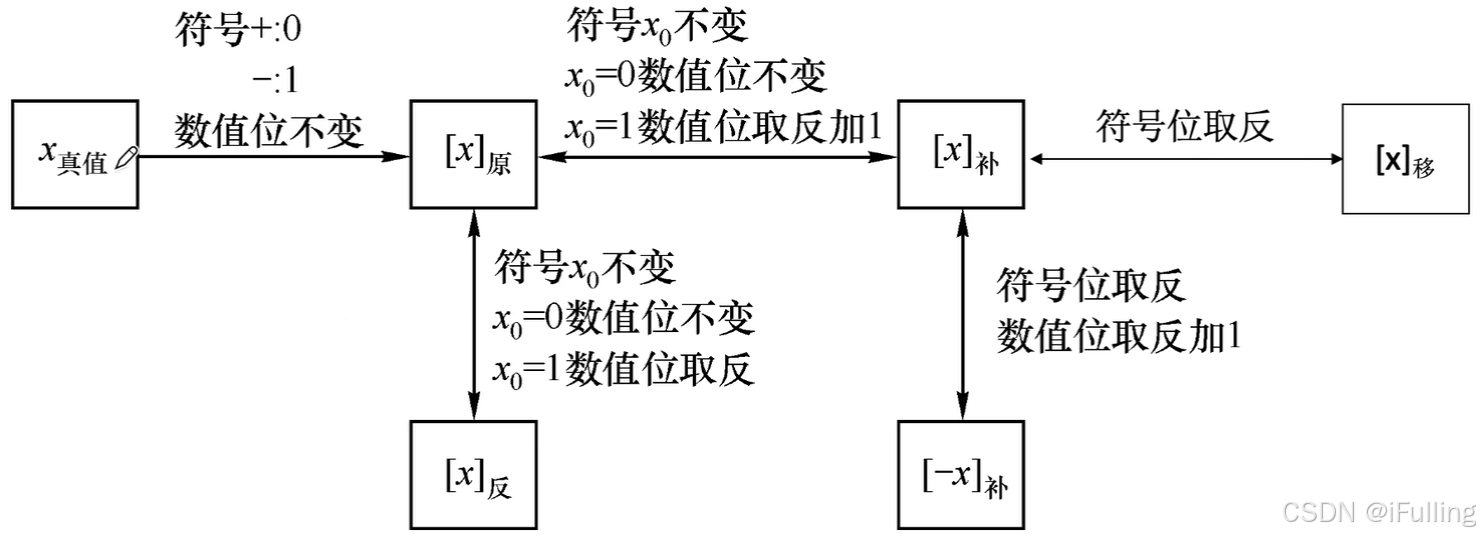
Ⅰ. 原码

• 原码：用尾数表示真值的绝对值，符号位 “0/1” 对应 “正/负”
• 定点整数原码：
  • 若机器字长为 $n+1$ 位，原码整数的表示范围（关于原点对称）：$$-(2^n-1)\le x\le 2^n-1$$
  • 真值 $0$ 有 $+0$ 和 $-0$ 两种形式

  真值（十进制）	原码（8位二进制）	说明
  +19D	00010011	符号位为 0（正数），数值部分为 19 的二进制 10011，高位补 0 凑满 8 位。
  -19D	10010011	符号位为 1（负数），数值部分与 +19 相同（10011），高位补 0 凑满 8 位。

  若机器字长为 8 位，-19 的原码可写为 [x]_原 = 1,0010011。
  若未指明机器字长，也可写为 [x]_原 = 1,10011

• 定点小数原码
  • 若机器字长为 $n+1$ 位，原码小数的表示范围（关于原点对称）：$$-(1-2^{-n})\le x\le 1-2^{-n}$$

  真值（十进制）	原码（8位二进制）	说明
  +0.75D	01100000	符号位为 0（正数），小数部分为 0.75 的二进制 11，低位补 0 凑满 8 位。
  -0.75D	11100000	符号位为 1（负数），小数部分与 +0.75 相同（11），低位补 0 凑满 8 位。

  若机器字长为 8 位，-0.75 的原码可写为 [x]_原 = 1.1100000。

Ⅱ. 反码

• 若符号位为 $0$，则反码与原码相同
• 若符号位为 $1$，则数值位全部取反
• 反码与原码的位数和表示范围一一对应，因此 $0$ 也有两种形式

  真值	原码	反码
  +0D	0,0000000	0,0000000
  -0D	1,0000000	1,1111111
  +19D	0,0010011	0,0010011
  -19D	1,0010011	1,1101100
  +0.75D	0.1100000	0.1100000
  -0.75D	1.1100000	1.0011111

反码只是原码转变为补码的一个中间状态，实际中并没有什么用

Ⅲ. 补码

• 正数的补码 = 原码
• 负数
  • 原码转补码：补码 = 原码取反，末位加一（反码末位 + 1）
  • 补码转原码：原码 = 补码取反，末位加一（方法一样）

  补码转原码更快的方法：最右边的 1 及其右边同原码，最右边的 1 的左边同反码

• [x]_补 转 [-x]_补：符号位、尾数全部取反，末位加一
• 补码的 $0$ 只有一种表示，即 00000000
  • 因此规定补码 1,0000000 = $-2^7$，补码 1.0000000 = $-1$
  • 若机器字长为 $n+1$ 位，补码整数的表示范围（比原码多表示一个 $-2^n$）：$$-2^n\le x\le 2^n-1$$
  • 若机器字长为 $n+1$ 位，补码小数的表示范围（比原码多表示一个 $-1$）：$$-1\le x\le 1-2^{-n}$$

真值	原码	反码	补码
+0D	0,0000000	0,0000000	0,0000000
-0D	1,0000000	1,1111111	0,0000000
+19D	0,0010011	0,0010011	0,0010011
-19D	1,0010011	1,1101100	1,1101101
+0.75D	0.1100000	0.1100000	0.1100000
-0.75D	1.1100000	1.0011111	1.0100000

补码的作用：使用补码可将减法操作转变为等价的加法，ALU 中无需集成减法器。执行加法操作时，符号位一起参与运算

Ⅳ. 移码

• 移码：在补码的基础上将符号位取反。
• 移码只能用于表示整数
• 移码和补码是一一对应的，因此表示范围与补码一样。
• 相比于补码的优势：表示的整数很方便对比大小
  

3. 类型转换

• C 语言中定点整数（int、short、long）是用补码的形式存储的
• 无符号数与有符号数：
  • 不改变数据内容，改变解释方式

  // x = 1110 1111 0001 1111
  short x = -4321;
  // 真值 x = -4321，y = 61215
  unsigned short y = (unsigned short)x;
  

• 长整数变短整数：
  • 高位截断，保留低位

  // a = 0x000286a1
  // b = 0xffff7751
  int a = 165537, b = -34991;
  // c = 0x86a1, d = 0x7751
  short c = (short)a, d = (short)b;
  

• 短整数变长整数：
  • 有符号数（符号扩展）：用符号位扩展高位（比如负号的符号位是 1，高位就补 1）

  0,1011010 → 0,00000000 1011010

  • 无符号数（零扩展）：高位补 0

  01011010 → 00000000 01011010

  • 长度扩展的应用场景：
    • ALU 的位数是固定的，运算前可能需要把短数据扩展为长数据
    • 通用寄存器位数是固定的，把数据存入寄存器时，可能需要进行长度扩展
    • 主存内的各种数据长度不一，有时需要把短数据扩展为长数据

三、数字电路

1. 逻辑门电路

• 逻辑门电路：用于处理二进制的逻辑运算
  • 基本逻辑运算：与、或、非
  • 复合逻辑运算：与非、或非、异或、同或（异或非）
  • 其他更复杂的…
    
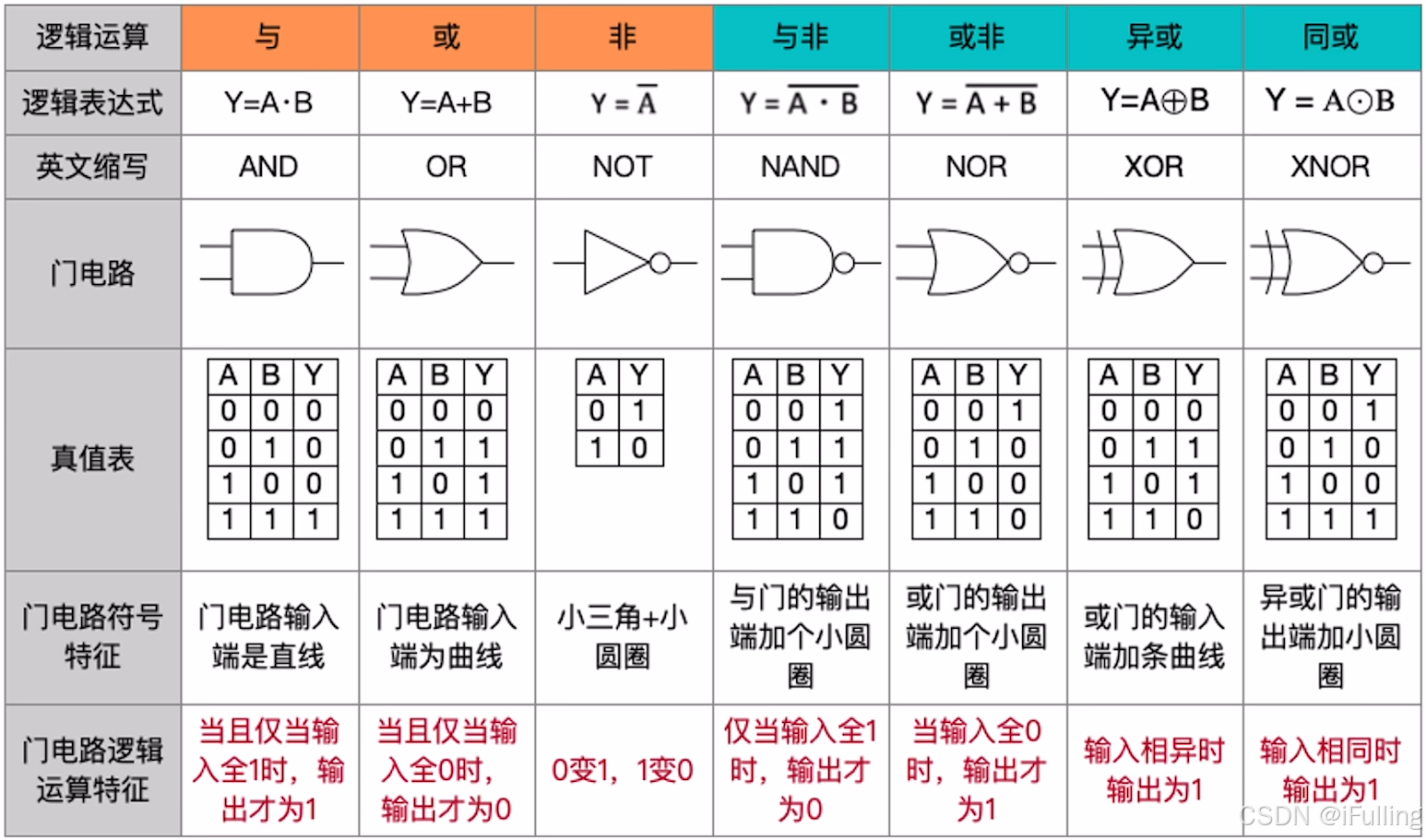
• 异或运算的应用：奇偶校验、二进制加法
• 多输入门电路：
  • 多输入或门：$Y=A+B+C+D$，当且仅当所有输入都为 0 时，输出才为 0（有 1 则 1）
  • 多输入与门：$Y=A\cdot B\cdot C\cdot D$，当且仅当所有输入都为 1 时，输出才为 1（全 1 才 1）
  • 多输入或非门：$Y=\overline{A+B+C+D}$，当且仅当所有输入都为 0 时，输出才为 1（全 0 才 1）
  • 多输入与非门：$Y=\overline{A\cdot B\cdot C\cdot D}$，当且仅当所有输入都为 1 时，输出才为 0（有 0 则 1）
• 逻辑运算优先级
  1. 非 > 与 > 或
  2. 有括号先算括号
  3. 非运算下面隐含一个括号

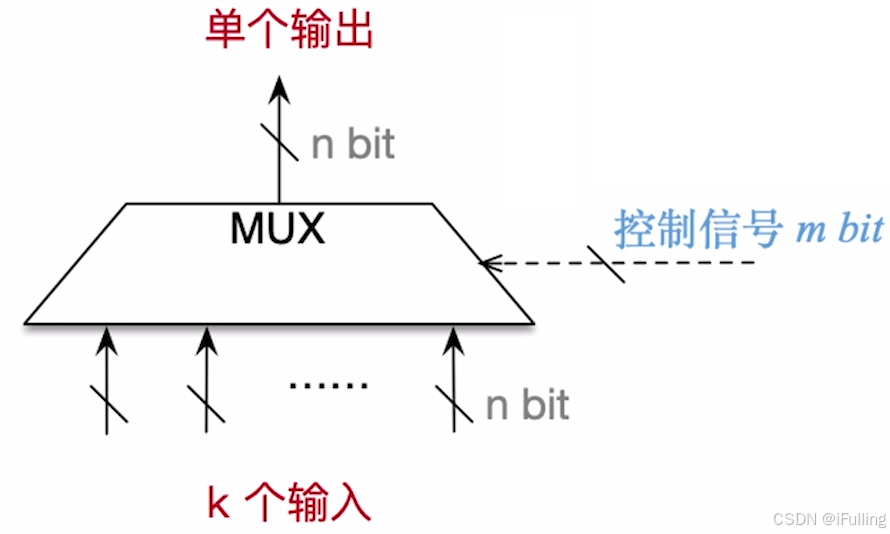
2. 多路选择器

• 多路选择器（Multiplexer，MUX）：在多个输入数据中，只允许其中一个数据通过 MUX，类似于电路的 “守门员”。
• 若有 $k$ 个输入，则控制信号的位数 $m\ge \lceil lo{g}_{2}k\rceil \text{ bit}$
• 有的多路选择器可能会预留一个控制信号，用于拦截所有输入

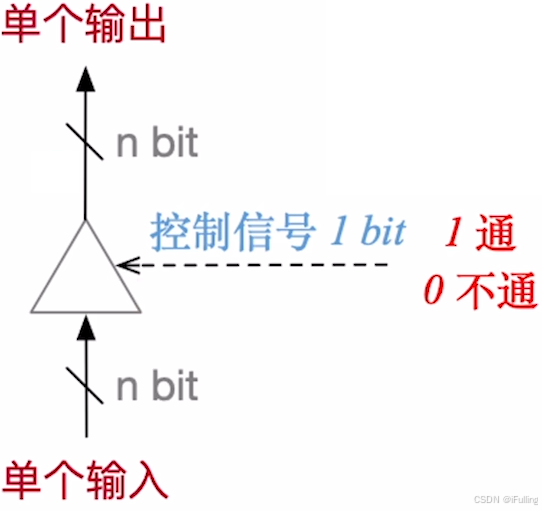
3. 三态门

• 三态门：根据控制信号决定是否让输入的数据通过。
• 三态门的控制信号通常只需要 1 bit，op = 1 表示允许数据通过，op = 0 表示不允许数据通过。

四、加法器

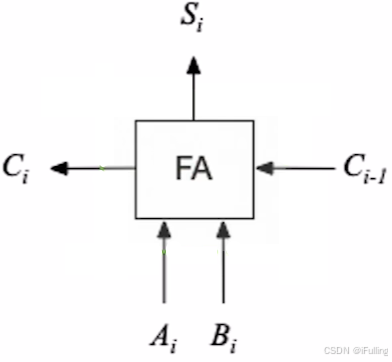
1. 一位全加器

• 一位全加器（FA，Full Adder），即只进行 1 bit 的加运算
  • 本位：进行运算的位
  • 进位：低位的加法溢出产生进位
  • 封装后的一位全加器 FA
    
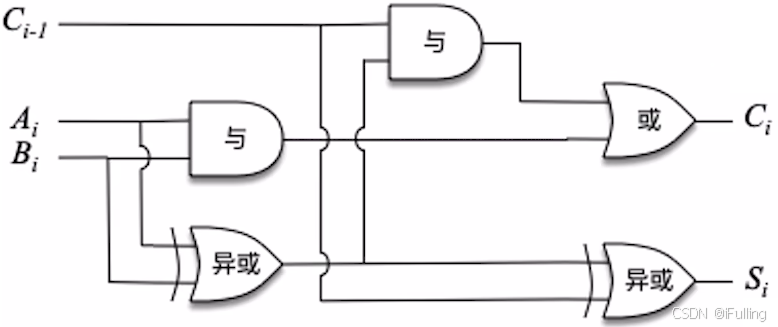
• 设被加数本位 $A_i$，加数本位 $B_i$，来自低位的进位 $C_{i-1}$，本为和 $S_i$，向高位的进位 $C_i$
  • 本为和：输入中有奇数个 1 时输出 1$$S_i=A_i\oplus B_i\oplus C_{i-1}$$
  • 向高位的进位：输入中至少 2 个 1 时输出 1$$C_i=A_i{B}_i+(A_i\oplus B_i)C_{i-1}$$
    

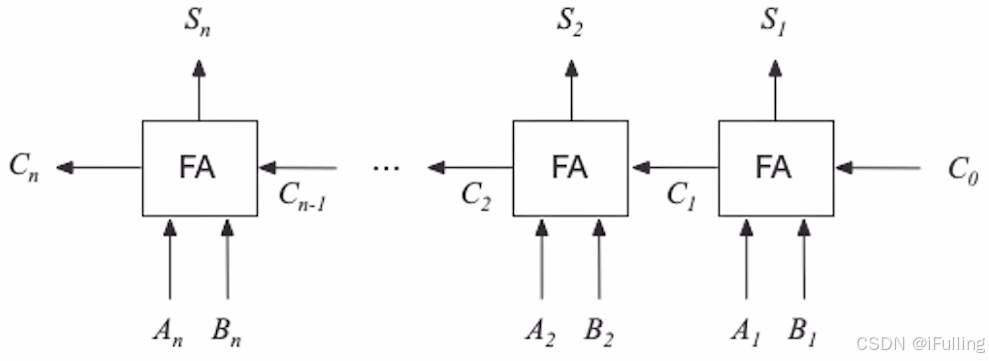
2. 并行加法器

• 并行加法器：两个输入端允许并行输入 n bit 进行加法运算
• 串行进位
  • 实现：将 n 个一位全加器简单串联，可支持 n bit 并行加
  • 缺点：进位信息是串行产生的，运算速度较慢
    
• 并行进位
  • 实现：对 “串行进位” 的加法器电路进行优化，增加 CLA（Carry-Lookahead Adder，先行进位加法器）部件
  • 优点：进位信息是并行产生的，运算速度更快
    

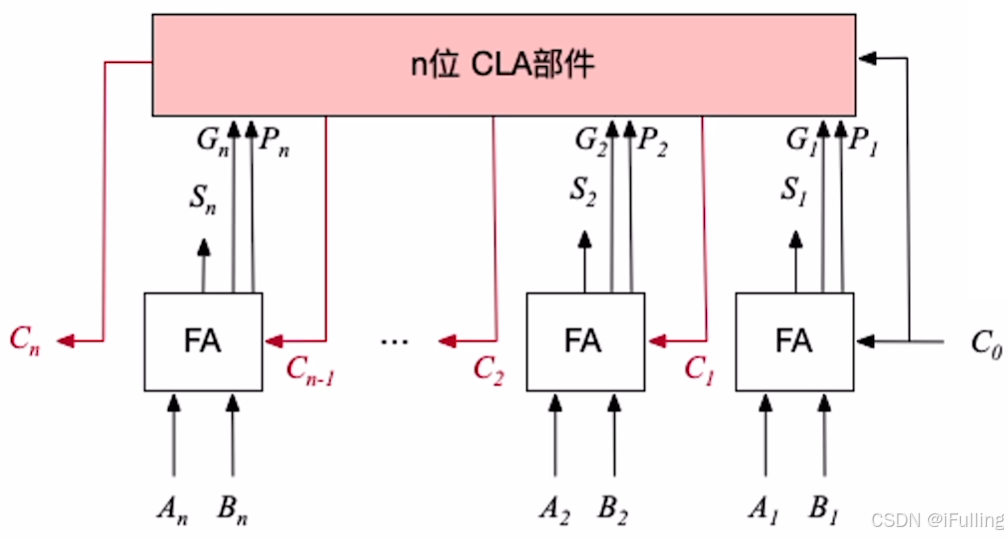
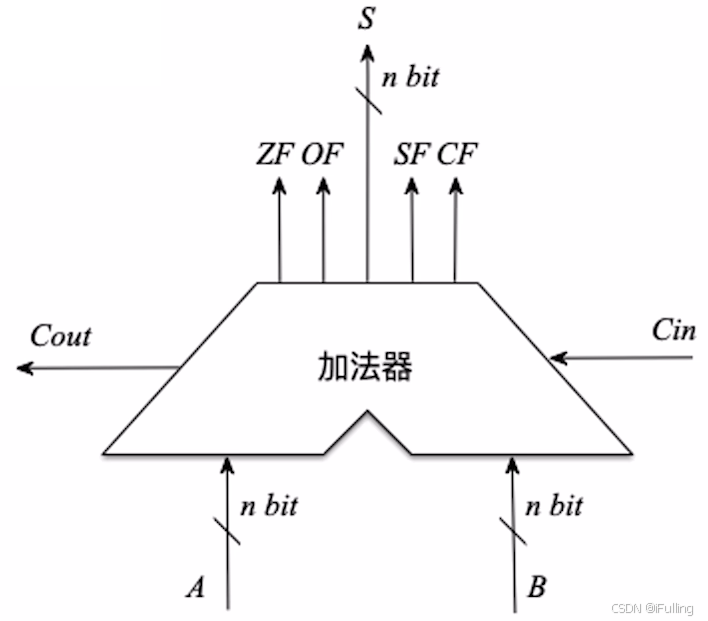
3. 带标志位的加法器

• 在并行加法器的基础上，增加电路逻辑，输出 OF、SF、ZF、CF 等标志位

  标志位	翻译	作用	含义
  OF	Overflow Flag，溢出标志	判断带符号数加减运算是否溢出	1 溢出、0 未溢出
  SF	Sign Flag，符号标志	判断带符号数加减运算结果的正负性	1 负 0 正
  ZF	Zero Flag，零标志	判断加减运算结果是否为 0	ZF = 1 表示运算结果为 0
  CF	Carry Flag，进位/借位标志	判断无符号数加减运算是否溢出	1 溢出、0 未溢出

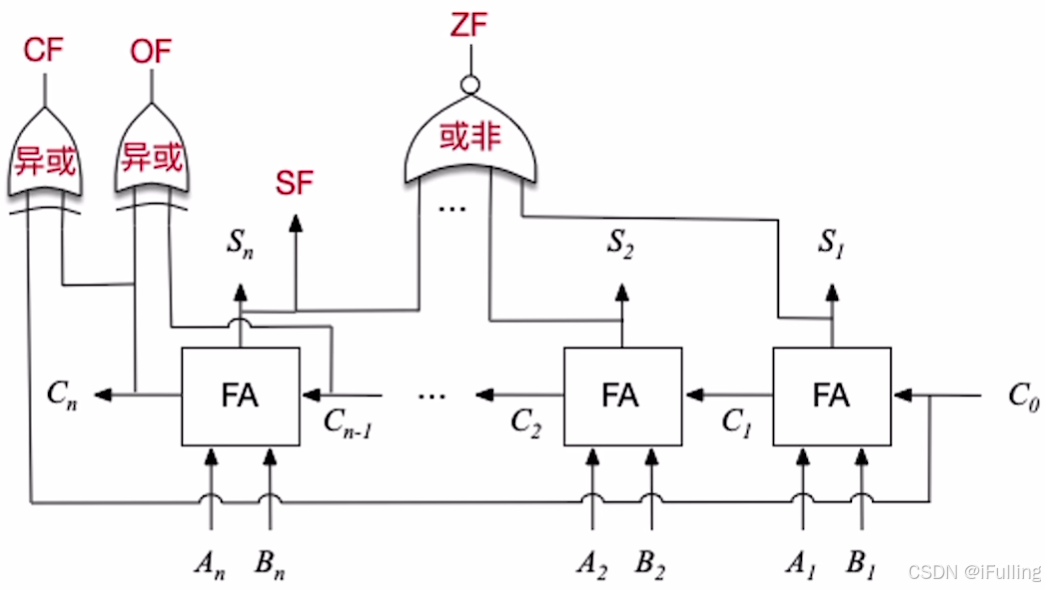
• 每个标志的运算规则：
  • OF，即最高位的进位 $\oplus$ 次高位的进位$$OF=C_n\oplus C_{n-1}$$
  • SF，取运算结果的最高位（符号位）$$SF=S_n$$
  • ZF，仅当运算结果所有 bit 全 0 时，ZF 才为 1，此时表示运算结果为 0$$ZF=\overline{S_n+\dots +S_2+S_1}$$
  • CF，反映无符号数加减运算是否溢出$$CF=C_{out}\oplus C_{in}=C_n\oplus C_0$$
    

五、算术逻辑单元 ALU

1. ALU 的作用

• CPU 由控制器、运算器组成：
  • 控制器负责解析指令，并根据指令功能发出相应的控制信号
  • 运算器负责对数据进行处理，如加减乘除等
• ALU（Arithmetic and Logic Unit，算术逻辑单元）是一种组合逻辑电路，实现了算术运算（加减乘除）、逻辑运算（与或非）等功能。因此 ALU 是运算器的核心
• 由于加减乘除等运算都要基于 “加法” 来实现，因此加法器是 ALU 的核心

2. ALU 的功能

• 算术运算：加、减、乘、除 等
• 逻辑运算：与、或、非、异或、移位 等
• 其他：求补码、直送 等
• 如上，总共支持 $k$ 种功能，那么控制信号位数 $m\ge \lceil lo{g}_{2}k\rceil$
• ALU 最简单的实现原理：多个功能电路 + MUX，通过控制信号选通 MUX 的某个线路

3. ALU 图示

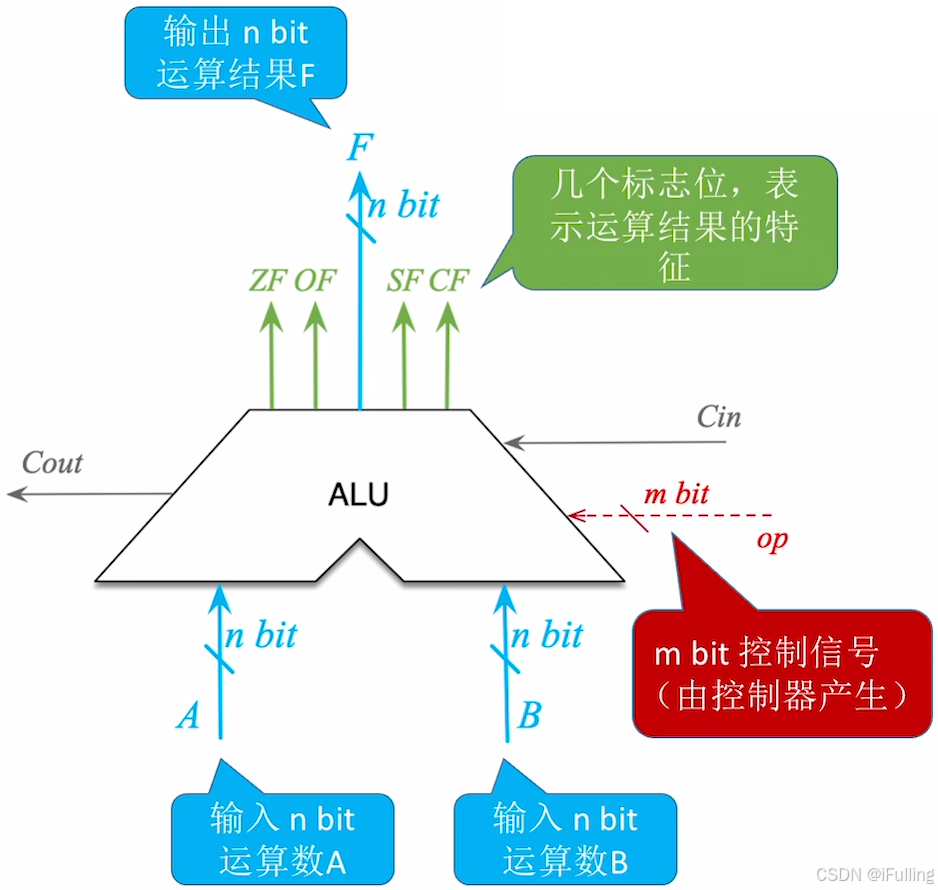
• 输入：
  • 控制信号 op（Operation）：由控制器产生，控制 ALU 进行指定运算，占 $m$ bit
    • m 的取值：如果 ALU 支持 $k$ 种功能，则控制信号位数 $m\ge \lceil lo{g}_{2}k\rceil$
  • ALU 的运算数、运算结果位数与计算机的机器字长相同
  • 或其他输入信息（如来自更低位的进位信息 Cin）
• 输出：
  • $n$ bit 的输出结果 F 与计算机机器字长相同
  • ZF/OF/SF/CF 标志位，用于表示本次运算结果的特征，这些标志信息通常会被送入 PSW（程序状态字寄存器，但有时也称为标志寄存器 FR，Flag Register）
  • 或其他输除信息（如往更高位的进位信息 Cout）