河南萌新联赛2025第（三）场：河南理工大学（补题）

前言

这次比赛只能说收获不少。

---

A.检讨

题目传送门：检讨


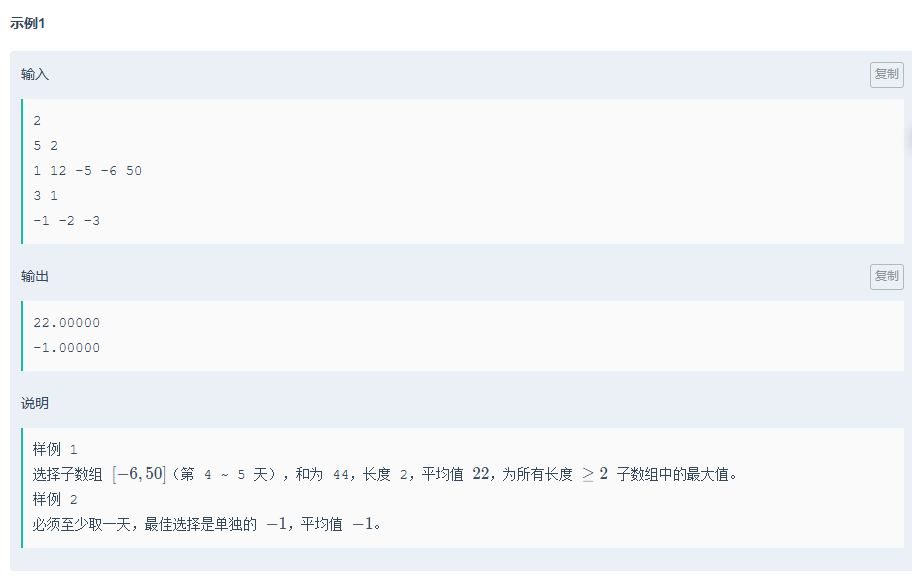
思路：就是二分+前缀和，当然，这个二分也不是太好想，
二分推理：
重要条件：

推导过程：
子数组 [i…j] 的平均值 ≥ m →
$$\frac{{\sum }_{k=i}^j{a}_k}{j-i+1}\ge m$$
两边同乘 (j-i+1)（正数，不改变不等号方向）→
$$\sum _{k=i}^j{a}_k\ge m\cdot (j-i+1)$$
变形为：
$$\sum _{k=i}^j(a_k-m)\ge 0$$
如果我们构造前缀和数组 sum，其中 sum[i] = (a₁ - m) + (a₂ - m) + … + (aᵢ - m)，那么子数组 [i…j] 满足条件等价于：
$$sum[j]-sum[i-1]\ge 0$$
为了找到长度 ≥ L 的子数组，我们需要：
1. 遍历到 j 时，在 [1…j-L] 范围内找最小的 sum[i-1]（记为 min_sum）。
2. 如果 sum[j] ≥ min_sum，说明存在子数组 [i…j]（长度 ≥ L）满足条件，返回 true。
这个前缀和，只能说非常的妙，通过

if (i >= L) {a = min(a, sum[i - L]); }

这一步取最小值将a锁定到了
「sum[0], sum[1], …, sum[i-L] 中的最小值」，确保我们能最容易地找到满足 sum[i] ≥ a 的情况
也就是:

if(sum[i]>=a)return true;

至于为什么是取最小值：
假设当前遍历到位置 j（即 i = j），此时需要考虑所有可能的起点 i，使得子数组 [i…j] 的长度 ≥ L（即 i ≤ j - L + 1）。
对应的前缀和条件是：
sum[j] - sum[i-1] ≥ 0 → sum[j] ≥ sum[i-1]。

要让这个不等式成立，最容易满足的情况是 sum[i-1] 尽可能小。
因此，我们只需要记录「i-1 在 [0, j-L] 范围内的最小 sum 值」（即 sum[i-L]，因为 i-1 = j-L 对应 i = j-L+1），然后判断 sum[j] 是否 ≥ 这个最小值即可。

同时这个前缀和很好的优化了时间复杂度，如果仅是判断>=L
1e6的时间复杂度通过嵌套循环将会超时；
如下：

double bruteForce() {double maxAvg = -1e18;// 枚举所有可能的起点for (int i = 1; i <= n; i++) {ll sum = 0;// 枚举所有可能的终点（保证长度 ≥ L）for (int j = i; j <= n; j++) {sum += s[j];int len = j - i + 1;if (len >= L) {  // 直接比较区间长度double avg = (double)sum / len;maxAvg = max(maxAvg, avg);}}}return maxAvg;
}

而前缀和：
当i >= L时，才开始记录前缀和的最小值（a = min(a, sum[i-L])）
此时i-L对应的起点，与当前i形成的区间长度恰好为L（i - (i-L+1) + 1 = L）
随着i增大，i-L也增大，自然包含了更长的区间（长度L+1、L+2等）
如下也就是核心代码：

bool check(double m)
{double a=1e10;for(ll i=1;i<=n;i++){sum[i]=sum[i-1]+s[i]-m;//通过上面的推导得到if(i>=L)a=min(a,sum[i-L]);//相当于区间长度尽量大于等于Lif(sum[i]>=a)return true;}return false;
}

完整代码:

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
const ll INF=1e18;
ll s[N];
double sum[N];
ll n,L;
bool check(double m)//核心判断条件
{double a=1e10;for(ll i=1;i<=n;i++){sum[i]=sum[i-1]+s[i]-m;if(i>=L)a=min(a,sum[i-L]);if(sum[i]>=a)return true;}return false;
}
void slove()
{cin>>n>>L;for(ll i=1;i<=n;i++){cin>>s[i];}double l=-1e8,r=1e8;double ans=0;while((r-l)>0.00001)//二分{double mid=(l+r)/2;if(check(mid)){l=mid;ans=mid;}elser=mid;}printf("%.8lf\n",ans);
}
signed main()
{IOS;ll t=1;cin>>t;while(t--)slove();return 0;
}

B.上海保卫战

题目传送门：上海保卫战


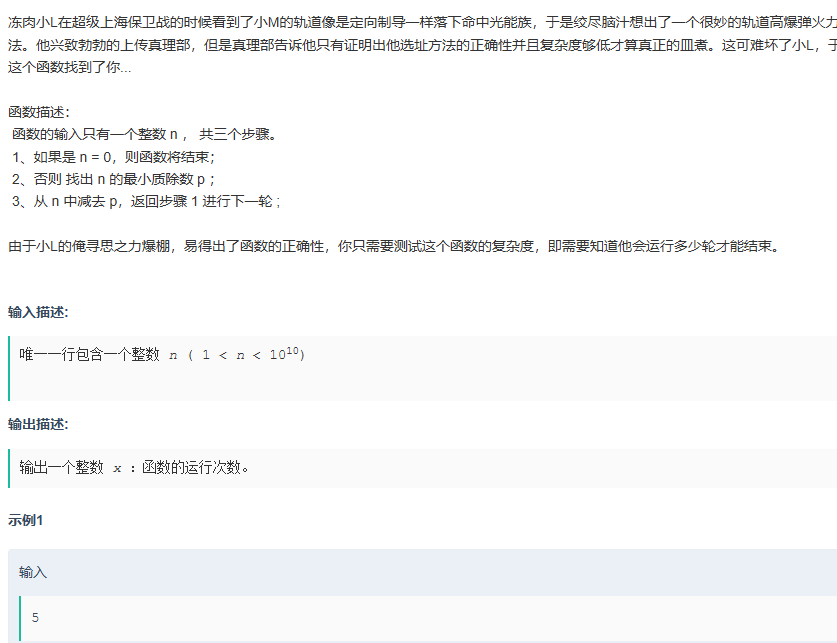
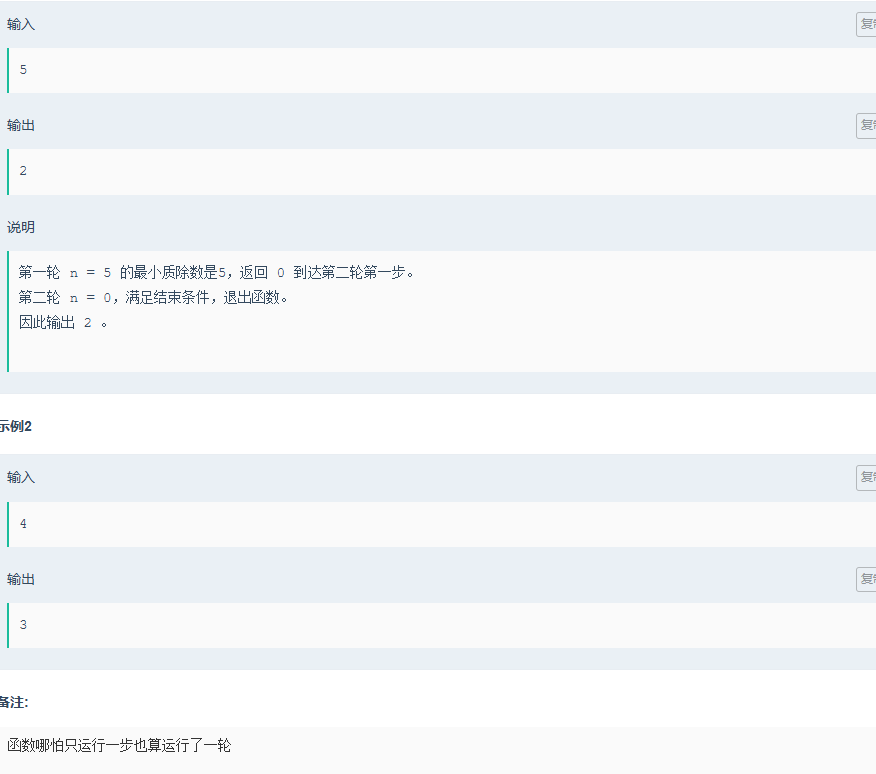
思路：其实题目只是一个幌子，通过观察，你就会发现，只需要，对其进行奇偶判断就行，如果是奇数，就减去最小质除数
因为奇-奇=偶，回到偶数情况。当然从这也学到了一个知识点
就是判断最小质除数:

ll get(ll x)
{for(ll i=2;i*i<=x;i++)if(x%i==0)return i;return x;
}

1. 质除数（质因数）的定义
如果一个数 i 满足：

i 是质数（只能被 1 和自身整除）
i 能整除 n（即 n % i == 0）

那么 i 就是 n 的质除数（质因数）。

2. 从小到大枚举的逻辑
由于是从小到大遍历，第一个满足 n % i == 0 的 i，必然是 n 的最小质除数，原因有两点：

i 是质数：如果 i 是合数，那它一定可以分解为更小的质数乘积（比如 i = 4 可分解为 2×2 ）。但我们是从小到大枚举的，若 i 是合数，那它的质因数会比 i 更小，且已经被枚举过了。因此，能通过 n % i == 0 找到的第一个 i，一定是质数。
i 是最小的：因为是从 2 开始往上找，第一个能整除 n 的质数，自然就是 n 的最小质除数。
完整代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
const ll INF=1e18;
ll get(ll x)//找到最小质除数
{for(ll i=2;i*i<=x;i++)if(x%i==0)return i;return x;
}
void slove()
{ll n;cin>>n;ll ans=1;ll m=0;if(n&1)//奇数情况{m=get(n);ans+=(n-m)/2+1;//变成偶数进行处理}else//偶数ans+=n/2;cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)slove();return 0;
}

E.星际争霸

题目传送门：星际争霸


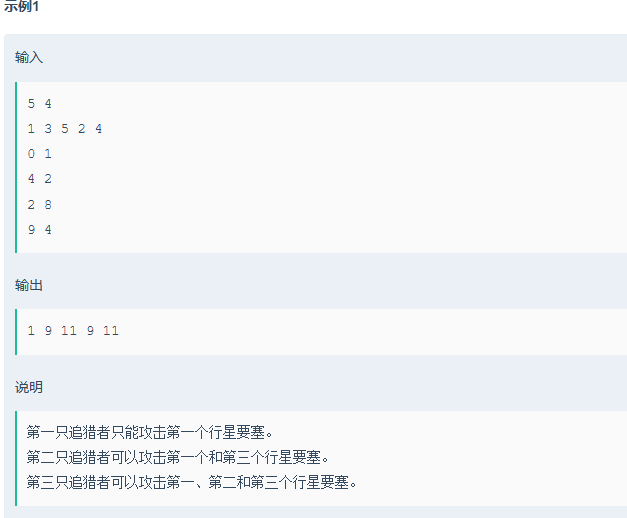
思路：就是前缀和的应用，这一题，本人想的比较复杂，就是先前缀和，然后排序，通过比较追猎者的攻击力与要塞的防御力来进行最大化，其实最开始，把这个题目与之前老鼠找洞的题，联想到一起了，想着直接把追猎者与要塞合在一起进行排序，但仔细想想，有太多细节，然后放弃了。
完整代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
const ll INF=1e18;
struct node{ll d,g;
}m1[N],sum[N],m[N];
bool cmd(node x,node y)
{return x.d<y.d;
}
bool cmd1(node x,node y)
{return x.g<y.g;
}
void slove()
{ll s,b;cin>>s>>b;for(ll i=1;i<=s;i++){cin>>m[i].d;m[i].g=i;}for(ll i=1;i<=b;i++){cin>>m1[i].d>>m1[i].g;}sort(m1+1,m1+b+1,cmd);//排序为了最大化前缀和sort(m+1,m+s+1,cmd);for(ll i=1;i<=b;i++){sum[i].d=m1[i].d;sum[i].g=m1[i].g+sum[i-1].g;}ll x=1;for(ll i=1;i<=s;i++){while(m[i].d>sum[x].d&&x<=b)//往后寻找第一个大于的防御力x++;if(m[i].d>=sum[x].d&&x<=b)m[i].d=sum[x].g;elsem[i].d=sum[x-1].g;}sort(m+1,m+s+1,cmd1);//按最初的位置排序for(ll i=1;i<=s;i++){cout<<m[i].d<<" ";}
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)slove();return 0;
}

当然还有更简便的就是前缀和加二分

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e5+10;
const ll INF=1e18;pii c[N];  // 存储防御力以及收获
ll sum[N];  // 前缀和数组
ll a[N];  // 存攻击力// 二分查找函数
ll bs(ll x, ll l, ll r)
{while(l < r){ll mid = l + r + 1 >> 1;if (c[mid].fi <= x) l = mid;else r = mid - 1;}return l;
}void slove()
{ll s, b;cin >> s >> b;for (ll i = 1; i <= s; i++)cin >> a[i];for (ll i = 1; i <= b; i++)cin >> c[i].fi >> c[i].se;sort(c + 1, c + b + 1);// 计算前缀和for (ll i = 1; i <= b; i++)sum[i] = sum[i - 1] + c[i].se;// 对每个s的数值进行查询并输出结果for (ll i = 1; i <= s; i++){ll id = bs(a[i], 0, b);//查找的是下标cout << sum[id] << " ";}cout << endl;
}signed main()
{IOS;ll t = 1;// cin >> t;while(t--)slove();return 0;
}

F.博弈

题目传送门：博弈


思路：
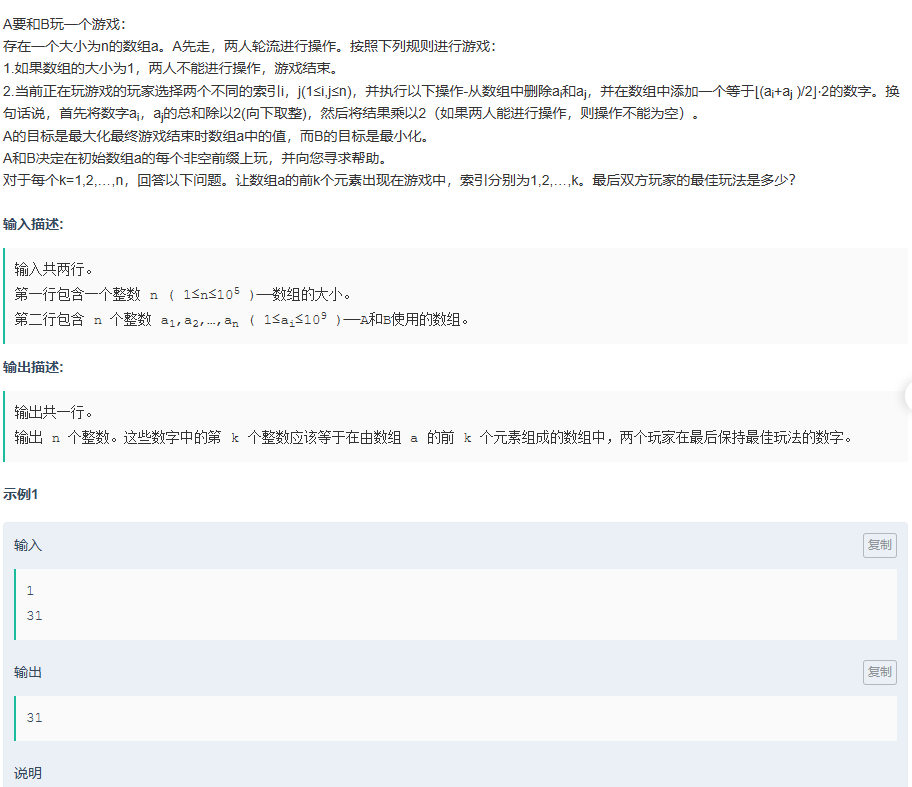
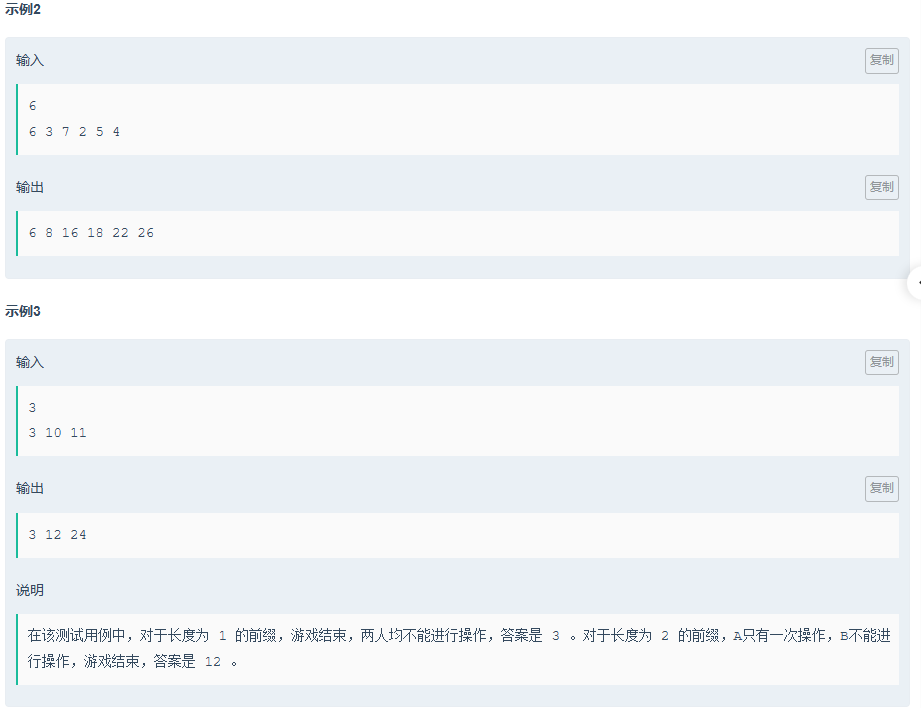
简单说，就是要你模拟 / 推导，对于数组的每个前缀，两个玩家按照 “一个想最大化、一个想最小化最终结果” 的策略博弈后，最终剩下的那个值是多少 。
要想最优，A同学必须选择两个偶数或者两个奇数，因为这两组相加之后还是偶数，这样就不会有损失，而B同学要想最小化，则必须是一奇一偶相加，这样才会损失1，由此，可以以3个奇数为一组，这样可以最优，由此，只需要统计各个阶段该区间内奇数的个数。
AC代码：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
ll sum[N];
ll a[N];
ll f[N];
void slove()
{ll n;cin>>n;if(n==1){ll x;cin>>x;cout<<x<<endl;return ;}for(ll i=1;i<=n;i++){cin>>a[i];sum[i]=sum[i-1]+a[i];if(a[i]%2!=0)f[i]++;f[i]=f[i]+f[i-1];//奇数个数前缀和}for(ll i=1;i<=n;i++){if(i==1)//当区间为1时不需要进行操作，直接输出就行{cout<<sum[i]<<" ";continue;}if(f[i]%3==1)//如果最后还剩余一个奇数，则需要多减去1cout<<sum[i]-1-f[i]/3<<" ";elsecout<<sum[i]-f[i]/3<<" ";}
}
signed main()
{IOS;ll t=1;// cin>>t;while(t--)slove();return 0;
}

G.方案数

题目传送门：方案数

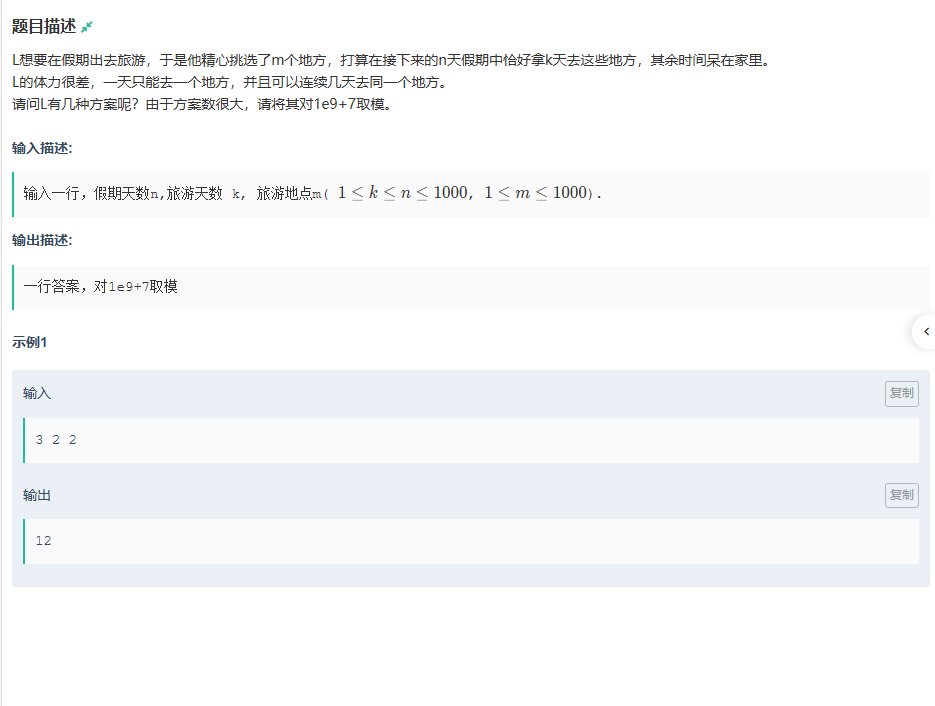
思路：
就是组合数，以及求k与的关系，写这一题的时候太无语了，组合数会求，通过杨辉三角推，乘法逆元，也用上了，同时还试了快速幂，最后就是错在了这一句，

完整代码：
第一种：杨辉三角递推

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e3+10;
const ll INF=1e18;
const ll mod=1e9+7;
ll s[N][N];
ll n,k,m;
void pre()
{for(ll i=1;i<=1001;i++){s[i][0]=1;s[i][i]=1;for(ll j=1;j<i;j++){s[i][j]=(s[i-1][j-1]+s[i-1][j])%mod;}}
}
void slove()
{pre();cin>>n>>k>>m;ll sum=1;for(ll i=1;i<=k;i++){sum=(sum*m)%mod;}ll ans=0;ans=s[n][k]%mod;cout<<ans*sum%mod<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)slove();return 0;
}

第二种;

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e3+10;
const ll INF=1e18;
const ll mod=1e9+7;
ll s[N][N];
ll n,k,m;
ll qmin(ll x,ll y)
{if(y==0)return 1;ll sum=1;while(y){if(y&1)sum=sum*x%mod;x=x*x%mod;y/=2;}return sum;
}
ll jie(ll n1,ll k1)
{ll ans=1;for(ll i=n1;i>n1-k1;i--){ans=(ans*i)%mod;}for(ll i=2;i<=k1;i++){ans=ans*qmin(i,mod-2)%mod;}return ans;
}
void slove()
{cin>>n>>k>>m;ll sum=1;for(ll i=1;i<=k;i++)sum=(sum*m)%mod;ll ans=jie(n,k)%mod;ans=ans%mod;cout<<ans*sum%mod<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)slove();return 0;
}

H.连续合规子串

题目传送门：连续合规子串


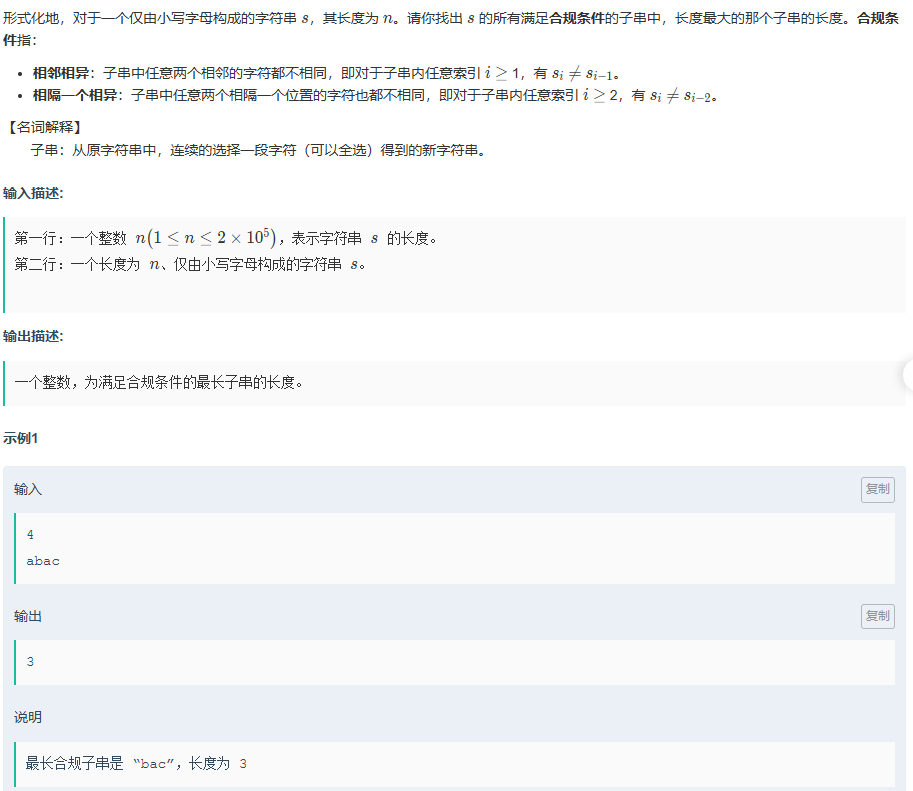
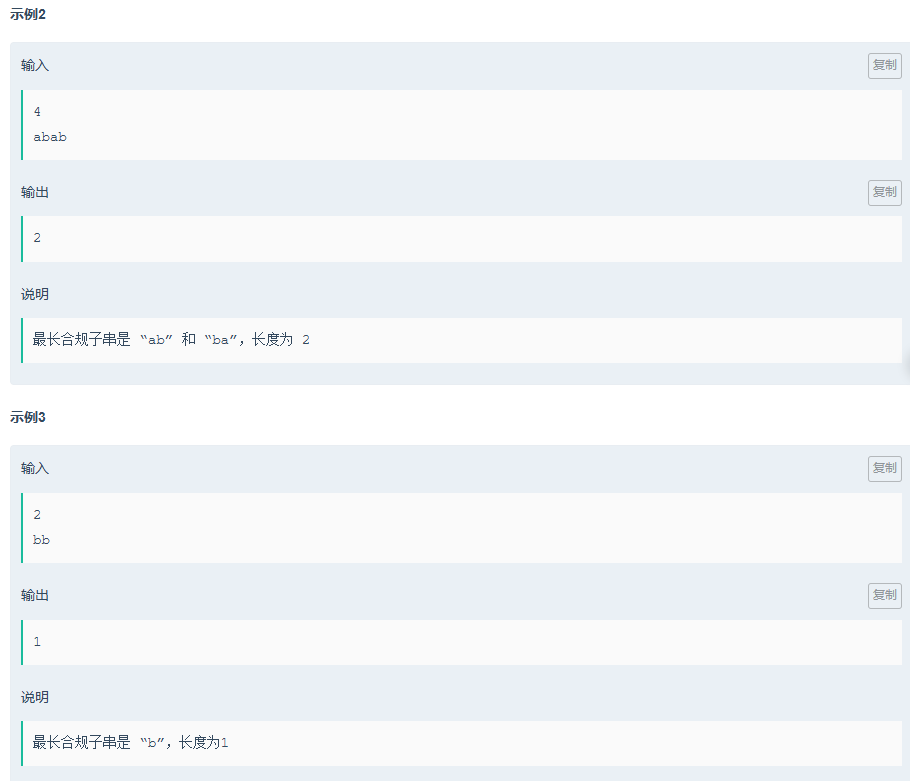
写这一题时，同样也快被折磨的快吐了，
写的时候一直把两个条件并在一起，其实并非如此，先去寻找远的，如果不满足就找相邻的，如果不满足，同样跳过当前的字符
完整代码;

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
const ll INF=1e18;
void slove()
{ll n;cin>>n;string s;cin>>s;if(n==1){cout<<1<<endl;return ;}if(n==2){if(s[1]!=s[0])cout<<2<<endl;elsecout<<1<<endl;return ;}ll ans=0;ll l=0;for(ll r=1;r<n;r++){if(s[r]==s[r-2])l=r-1;if(s[r]==s[r-1])l=r;ans=max(ans,r-l+1);}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)slove();return 0;
}

K.魔法音符

题目传送门：魔法音符


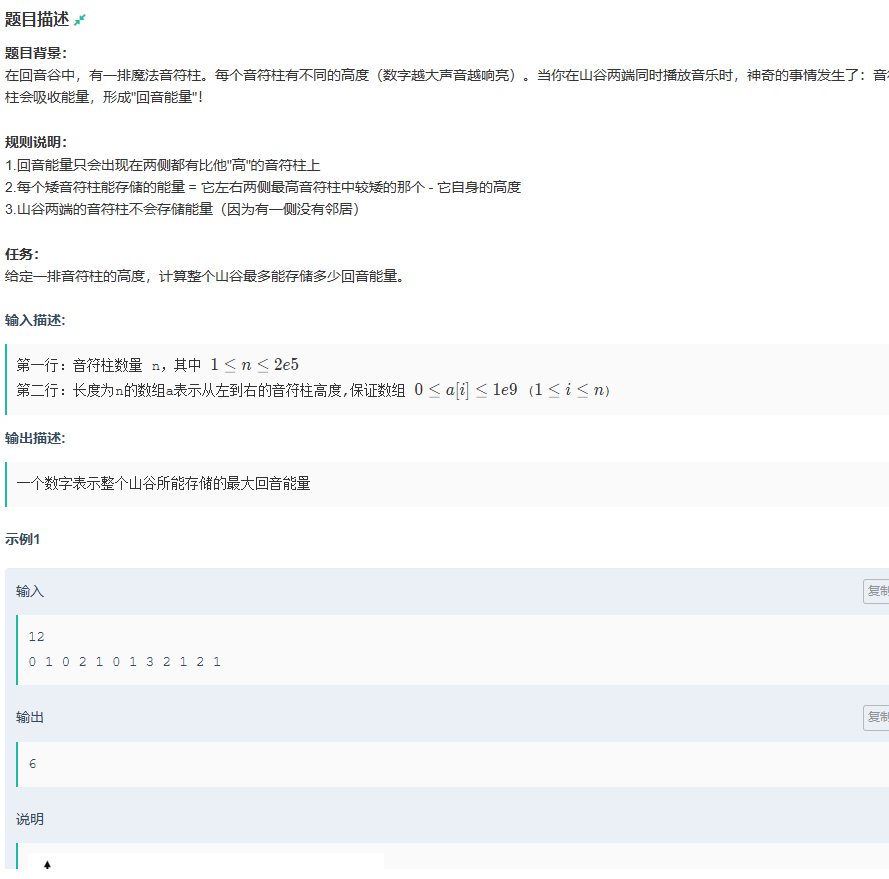
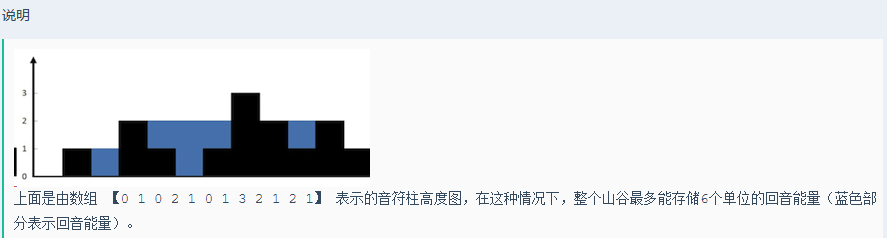
看见这一题时，第一眼就想到了接雨水，但是当时忘记了怎么写了，就琢磨了半天，好在最后写出来，要写不出来，就丢脸丢到家了，当比赛结束时，看了别人代码，才知道，原来，可以通过预处理来解决，嗯，又学到了一点。
完整代码：
第一种单调栈：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
const ll INF=1e18;
ll s[N];
void slove()
{ll n;cin>>n;for(ll i=1;i<=n;i++)cin>>s[i];stack<ll>p;ll ans=0;p.push(1);for(ll i=2;i<=n;i++){while(!p.empty()&&s[p.top()]<s[i]){ll r=i;ll x=p.top();p.pop();if(p.empty())break;ll h=min(s[p.top()]-s[x],s[i]-s[x]);ll l=p.top();ans=ans+(r-l-1)*h;}p.push(i);}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)slove();return 0;
}

第二种预处理：

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define endl '\n'
#define pii pair<ll,ll>
#define fi first
#define se second
const ll N=1e6+10;
const ll INF=1e18;
ll a[N];
ll b[N];
ll c[N];
void slove()
{ll n;cin>>n;ll ans=0;for(ll i=1;i<=n;i++){cin>>a[i];}b[1]=a[1];for(ll i=1;i<=n;i++){b[i]=max(b[i-1],a[i]);}c[n]=a[n];for(ll i=n-1;i>=1;i--){c[i]=max(c[i+1],a[i]);}for(ll i=1;i<=n;i++){ans+=min(b[i],c[i])-a[i];}cout<<ans<<endl;
}
signed main()
{IOS;ll t=1;//cin>>t;while(t--)slove();return 0;
}

---

总结

通过这场比赛，收获不少，写的时候，好像找到了，刚进入大一时对于一道题百思不得其解，最后通过答案，找到了自己的错误，那种新鲜感让人上瘾，希望这种感觉延迟下去。

---