【数据结构初阶】--二叉树选择题专辑


🔥个人主页:@草莓熊Lotso
🎬作者简介:C++研发方向学习者
📖个人专栏: 《C语言》 《数据结构与算法》《C语言刷题集》《Leetcode刷题指南》
⭐️人生格言:生活是默默的坚持,毅力是永久的享受。
前言: 这一篇博客是二叉树的选择题专辑,会给大家分享一下选择题中的知识点和做题思路,大家可以自己去做一下,顺便巩固一下知识点。
目录
二叉树选择题
二叉树的性质选择题:
链式二叉树的遍历选择题:
二叉树选择题
二叉树性质:
对任何⼀棵二叉树, 如果度为 0 其叶结点个数为, 度为 2 的分支结点个数为
,则有
性质证明过程如下:
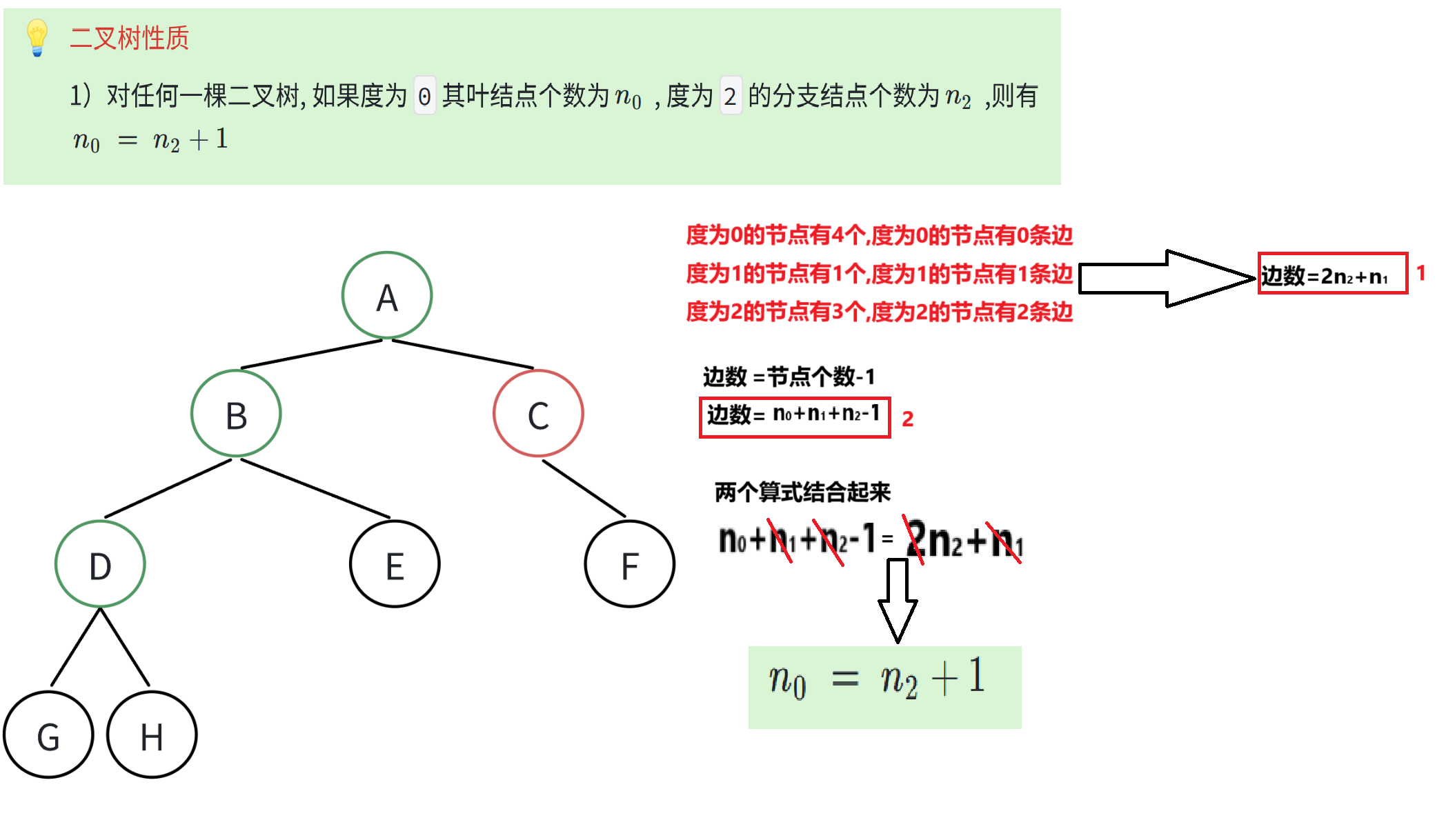
- 2a+b = a+b+c-1 ,即: a = c-1
二叉树的性质选择题:
1.某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为(B)
A.不存在这样的二叉树 B.200 C.198 D.199
由于二叉树的性质
可知,有199个度为2的结点,这二叉树的叶子结点个数为199+1=200。
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A)
A.n B.n+1 C.n-1 D.n/2
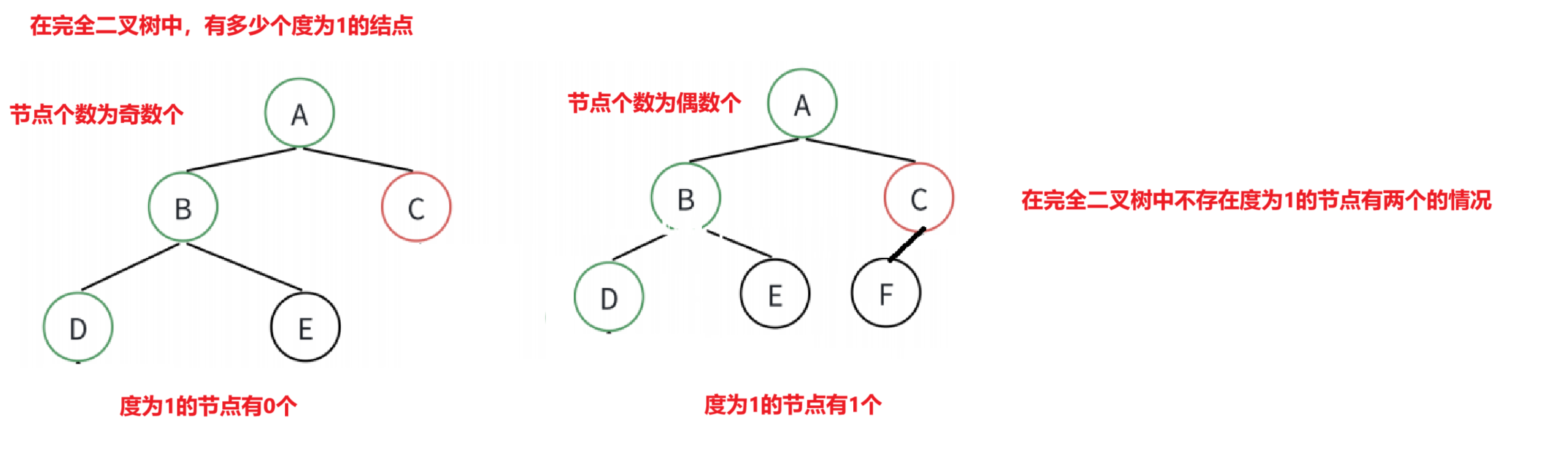
因为
所以
在完全二叉树中,度为1的节点要么为0,要么为1
结果为
或
,所以算式1算出来结果不为整数故我们按算式2的来,最终叶子结点个数为n
3.⼀棵完全二叉树的结点数为531个,那么这棵树的高度为(B)
A.11 B.10 C.8 D.12
前9层节点总个数=2^9-1= 511
我们这个完全二叉树的结点个数为531,所以高度是有10层,且最后一层的结点个数(叶子结点个数)为531-511=20个。
4.⼀个具有767个结点的完全二叉树,其叶子结点个数为(B)
A.383 B.384 C.385 D.386
n0+n1+n2=767 且n0=n2+1,n2=n0-1
所以n0+n0+n1-1=767
完全二叉树中总结点个数为奇数个,所以n1为0
故2n0=768 n0=384
综上所述,叶子结点个数为384个
链式二叉树的遍历选择题:
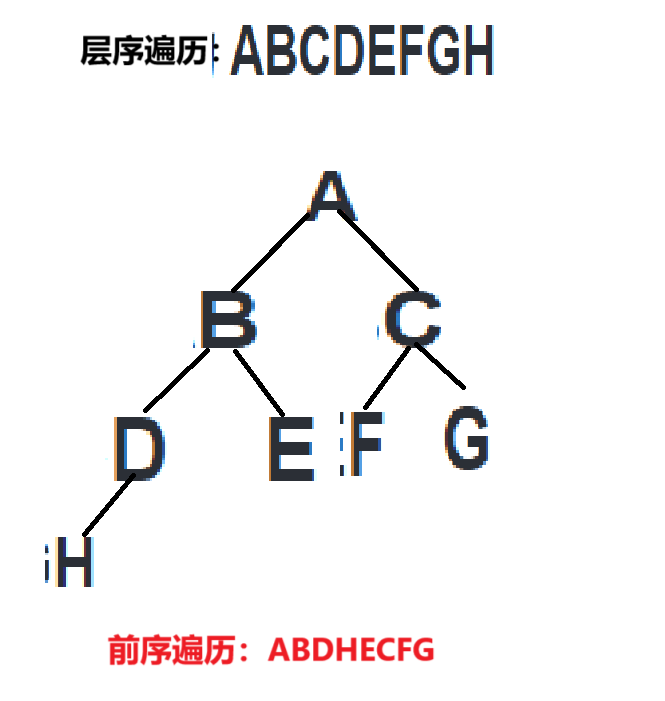
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为(A)
A. ABDHECFG
B. ABCDEFGH
C. HDBEAFCG
D. HDEBFGCA
我们先根据层序遍历序列画出这颗树,然后再通过画出来的树求出它的前序遍历序列
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为(A)
先序遍历就是前序遍历其第一个结点肯定就是根结点,所以这题根节点就是E可以直接选A。
补充一下,如果是后序遍历的话根结点一定是最后一个结点。中序遍历的话左右孩子结点分别在根节点两侧(具体是那两个需要确定)。
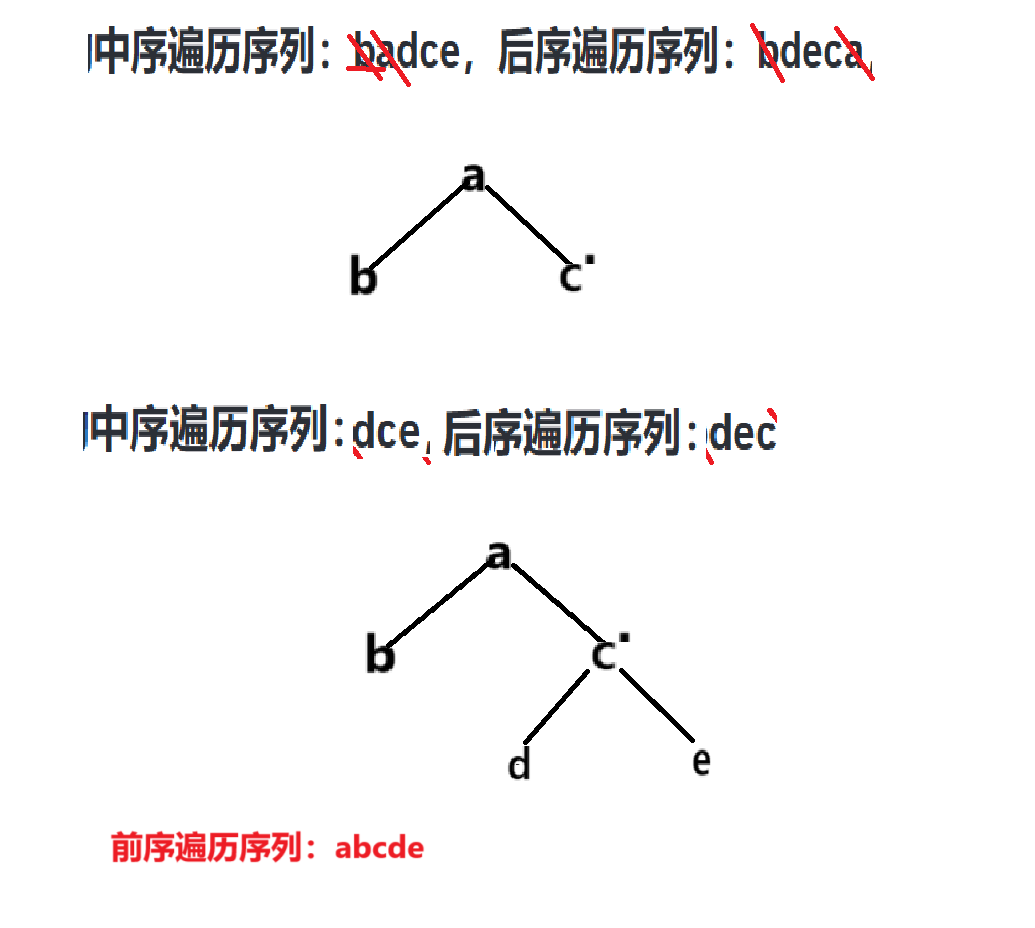
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为(D)
根据后序遍历确定了根结点为a,再看中序遍历,左边除了b就没有了所以b肯定为a的左孩子结点,dce中c为a的右孩子结点(我们可以在和中后序遍历中都去掉a,b。当前后序序列中最后一个为c,所以c是a的右孩子结点也是d和e的根结点)。根据此时的中序遍历序列可知c的左右都只有一个结点了,所以就直接可以确定了。
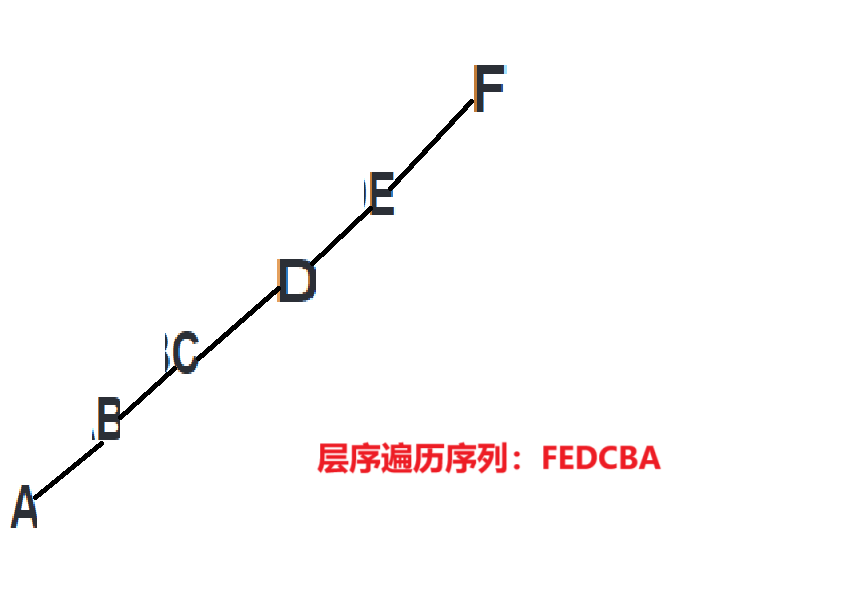
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同⼀层从左到右的序列为(A)
跟上题思路一样,先根据后序和中序遍历还原二叉树,再求出它的层序遍历。这里我们就不再描述具体过程了,大家直接看图
往期回顾:
【数据结构初阶】--二叉树(三)
【数据结构初阶】--二叉树(四)
【数据结构初阶】--二叉树(五)
【数据结构初阶】--二叉树(六)
结语:选择题的特辑就到此结束了,其实二叉树的选择题还是很有学习的意义的,对巩固二叉树的知识点很有帮助,如果文章对你有帮助的话,欢迎评论,点赞,收藏加关注,感谢大家的支持。