当前位置：首页 > news >正文

LeetCode 85：最大矩形

news 2025/8/2 14:10:52

LeetCode 85：最大矩形

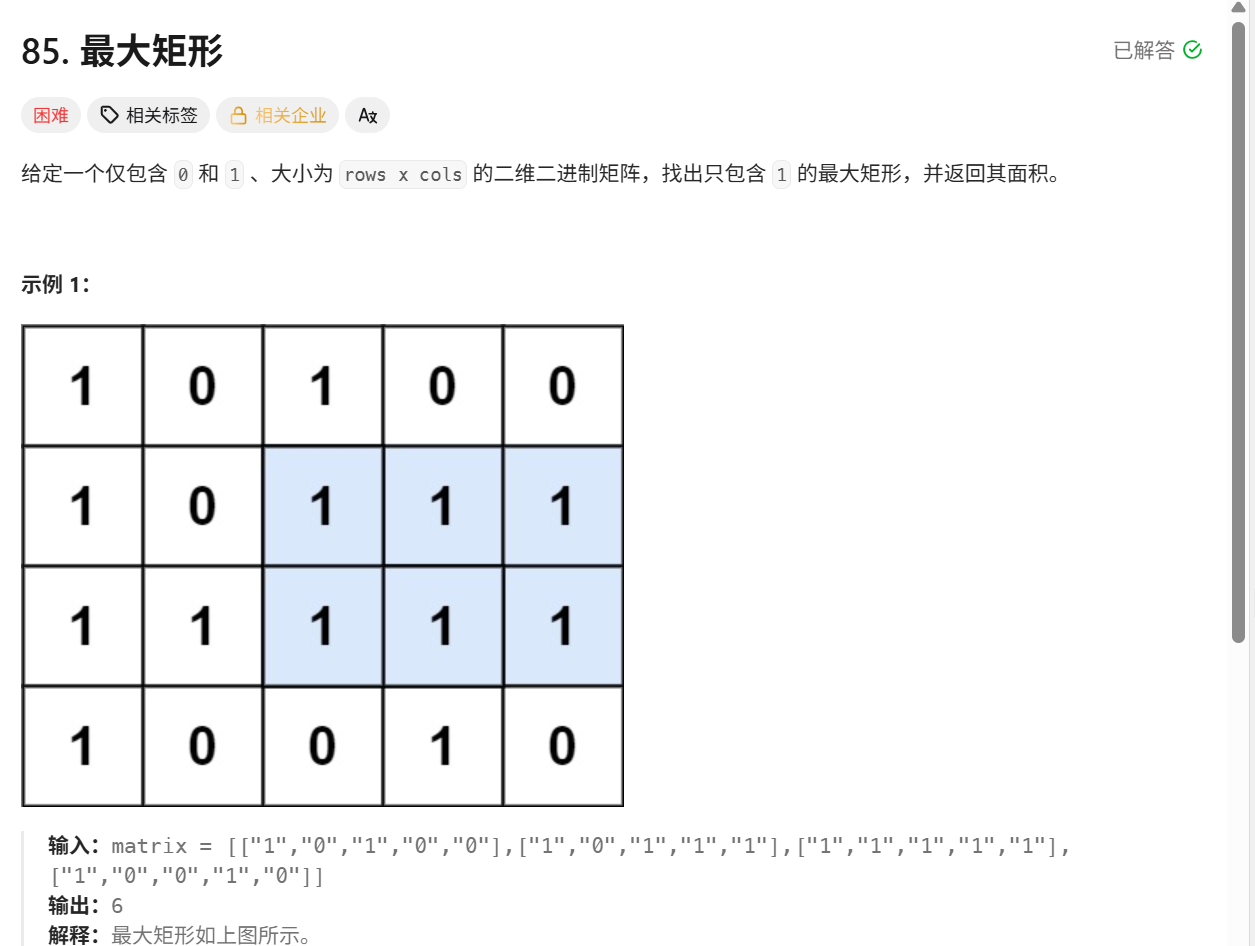
在这里插入图片描述

问题本质与核心挑战

给定仅含 0 和 1 的二维矩阵，需找到全由 1 组成的最大矩形面积。核心挑战：

直接枚举所有矩形（O(n²m²)）效率极低；
需通过 “逐行构建柱状图 + 单调栈求最大面积” 优化，将复杂度降为 O(rows×cols)。

核心思路：二维 → 一维的转化

1. 柱状图的构建

对矩阵的每一行，计算以该行作为底边的“柱状图高度”：

若当前单元格为 1，则高度为上方连续 1 的个数 + 1（继承上一行的高度）；
若当前单元格为 0，则高度重置为 0（无法形成垂直连续的 1）。

2. 复用柱状图最大面积算法（LeetCode 84题）

对每一行构建的柱状图，使用 单调栈 快速计算其最大矩形面积（时间复杂度 O(cols)），最终取所有行的最大值。

算法步骤详解（以示例 `matrix = [[1,0,1,0,0],[1,0,1,1,1],[1,1,1,1,1],[1,0,0,1,0]]` 为例）

步骤 1：初始化变量与高度数组

int rows = matrix.length;   // 行数（4）
int cols = matrix[0].length; // 列数（5）
int[] height = new int[cols]; // 记录当前行的柱状图高度
int maxArea = 0; // 全局最大面积

步骤 2：逐行构建柱状图，计算最大面积

遍历每一行，更新 height 数组，并调用 largestRectangleArea 计算当前行的最大面积：

for (int i = 0; i < rows; i++) {// 更新当前行的高度数组for (int j = 0; j < cols; j++) {height[j] = (matrix[i][j] == '1') ? height[j] + 1 : 0;}// 计算当前柱状图的最大面积，更新全局最大值maxArea = Math.max(maxArea, largestRectangleArea(height));
}

示例演示（行2的 height 构建）：

行2的 matrix 为 ["1","1","1","1","1"]：
- j=0：matrix[2][0]='1' → height[0] = height[0](2) + 1 = 3；
- j=1：matrix[2][1]='1' → height[1] = height[1](0) + 1 = 1；
- 最终 height = [3,1,3,2,2]（对应柱状图高度）。

步骤 3：单调栈计算柱状图最大面积（复用LeetCode 84题逻辑）

private int largestRectangleArea(int[] heights) {Stack<Integer> stack = new Stack<>(); // 存储索引，保持高度递增int max = 0;int n = heights.length;for (int i = 0; i < n; i++) {// 当前高度 < 栈顶高度 → 弹出栈顶，计算面积while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) {int top = stack.pop();int h = heights[top];int left = stack.isEmpty() ? -1 : stack.peek(); // 左边界int right = i; // 右边界max = Math.max(max, h * (right - left - 1));}stack.push(i); // 当前索引入栈}// 处理栈中剩余元素（右边界为n）while (!stack.isEmpty()) {int top = stack.pop();int h = heights[top];int left = stack.isEmpty() ? -1 : stack.peek();int right = n;max = Math.max(max, h * (right - left - 1));}return max;
}

示例演示（行2的 height = [3,1,3,2,2]）：

步骤	栈状态	操作	计算的面积	局部max
`i=0`（height=3）	`[0]`	压入0	-	`0`
`i=1`（height=1）	`[1]`	弹出0 → 面积 `3×(1-(-1)-1)=3`	`3`	`3`
`i=2`（height=3）	`[1,2]`	压入2	-	`3`
`i=3`（height=2）	`[1,3]`	弹出2 → 面积 `3×(3-1-1)=3`；弹出1 → 面积 `1×(3-(-1)-1)=3`	`3,3`	`3`
`i=4`（height=2）	`[3,4]`	压入4	-	`3`
遍历结束，处理栈	`[]`	弹出4 → 面积 `2×(5-3-1)=2`；弹出3 → 面积 `2×(5-1-1)=6`	`2,6`	`6`

完整代码（Java）

import java.util.Stack;class Solution {public int maximalRectangle(char[][] matrix) {if (matrix == null || matrix.length == 0) {return 0;}int rows = matrix.length;int cols = matrix[0].length;int[] height = new int[cols]; // 记录当前行的柱状图高度int maxArea = 0;for (int i = 0; i < rows; i++) {// 逐列更新高度：当前为'1'则累加，否则置0for (int j = 0; j < cols; j++) {height[j] = (matrix[i][j] == '1') ? height[j] + 1 : 0;}// 计算当前行的最大矩形面积，更新全局最大值maxArea = Math.max(maxArea, largestRectangleArea(height));}return maxArea;}// 复用LeetCode 84题的单调栈解法，计算柱状图的最大矩形面积private int largestRectangleArea(int[] heights) {Stack<Integer> stack = new Stack<>();int maxArea = 0;int n = heights.length;for (int i = 0; i < n; i++) {// 维护单调递增栈：当前高度 < 栈顶高度时，弹出栈顶计算面积while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) {int topIndex = stack.pop();int h = heights[topIndex];// 左边界：栈空则为-1，否则为新栈顶int left = stack.isEmpty() ? -1 : stack.peek();// 右边界：当前索引iint right = i;int width = right - left - 1;maxArea = Math.max(maxArea, h * width);}stack.push(i); // 当前索引入栈}// 处理栈中剩余元素（右边界为n）while (!stack.isEmpty()) {int topIndex = stack.pop();int h = heights[topIndex];int left = stack.isEmpty() ? -1 : stack.peek();int right = n;int width = right - left - 1;maxArea = Math.max(maxArea, h * width);}return maxArea;}
}