2023年数学建模国赛C题第一问解答

记录奋斗路上的点滴,
希望能帮到一样刻苦的你!
如有不足欢迎指正!
共同学习交流!
🌎欢迎各位→点赞 👍+ 收藏⭐ + 留言📝
来路无可眷恋,值得期待的只有前方!
一起加油!

2023年数学建模国赛C题第一问解答
在2023年数学建模国赛C题中,第一问主要涉及对蔬菜销售数据的分析,包括品类分析、单品分析和时间序列预测。
问题分析
第一问主要需要完成以下几个任务:
- 品类分析:包括不同品类销量分布差异的K-S检验和相关性分析
- 单品分析:筛选主要单品并进行相关性分析和聚类分析
- 时间序列分析:对特定品类进行销量预测
数据预处理
首先需要加载和预处理数据:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rcParams
from scipy import stats
from statsmodels.tsa.statespace.sarimax import SARIMAX
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.preprocessing import StandardScaler
from tqdm import tqdm
import sys# 设置中文字体支持
config = {"font.family": 'SimHei',"font.size": 12,"axes.unicode_minus": False,
}
rcParams.update(config)# 数据加载
att1_path = '附件1.xlsx'
att2_path = '附件2.xlsx'# 读取商品分类信息
prod_categories = pd.read_excel(att1_path, sheet_name='Sheet1')
prod_categories.columns = ['单品编码', '单品名称', '分类编码', '分类名称']# 读取销售流水数据
sales_data = pd.read_excel(att2_path)
sales_data = sales_data.iloc[:, [0, 2, 3]] # 选择需要的列
sales_data.columns = ['销售日期', '单品编码', '销量(千克)']
sales_data.rename(columns={'销售日期': '日期'}, inplace=True)# 合并数据
merged_data = pd.merge(sales_data, prod_categories, on='单品编码', how='left')
异常值处理
采用箱线图法处理异常值:
def handle_outliers(df, group_col, value_col):groups = df[group_col].unique()cleaned_data = []for group in tqdm(groups, desc="处理异常值", file=sys.stdout):group_data = df[df[group_col] == group].copy()q1 = group_data[value_col].quantile(0.25)q3 = group_data[value_col].quantile(0.75)iqr = q3 - q1lower_bound = q1 - 1.5 * iqrupper_bound = q3 + 1.5 * iqr# 用中位数替换异常值median_val = group_data[value_col].median()group_data.loc[:, value_col] = group_data[value_col].apply(lambda x: median_val if x < lower_bound or x > upper_bound else x)cleaned_data.append(group_data)return pd.concat(cleaned_data)# 处理品类级别异常值
category_data = merged_data.groupby(['日期', '分类名称'])['销量(千克)'].sum().reset_index()
cleaned_category_data = handle_outliers(category_data, '分类名称', '销量(千克)')
品类分析
K-S检验
使用K-S检验分析不同品类销量分布的差异:
# 获取所有品类名称
categories = cleaned_category_data['分类名称'].unique()print(f"\n=== 开始K-S检验 ===")
print(f"需要进行两两比较的品类组合数: {len(categories)*(len(categories)-1)//2}")ks_results = []# 使用tqdm包装双重循环
for i in tqdm(range(len(categories)), desc="K-S检验进度", file=sys.stdout):for j in range(i + 1, len(categories)):cat1 = categories[i]cat2 = categories[j]data1 = cleaned_category_data[cleaned_category_data['分类名称'] == cat1]['销量(千克)']data2 = cleaned_category_data[cleaned_category_data['分类名称'] == cat2]['销量(千克)']# 执行K-S检验statistic, p_value = stats.ks_2samp(data1, data2)ks_results.append({'品类1': cat1,'品类2': cat2,'统计量': statistic,'p值': p_value})ks_df = pd.DataFrame(ks_results)
print("不同品类销量分布K-S检验结果:")
print(ks_df)
相关性分析
计算品类销量的相关系数矩阵:
# 创建透视表
pivot_data = cleaned_category_data.pivot(index='日期', columns='分类名称', values='销量(千克)'
).fillna(0)# 计算相关系数
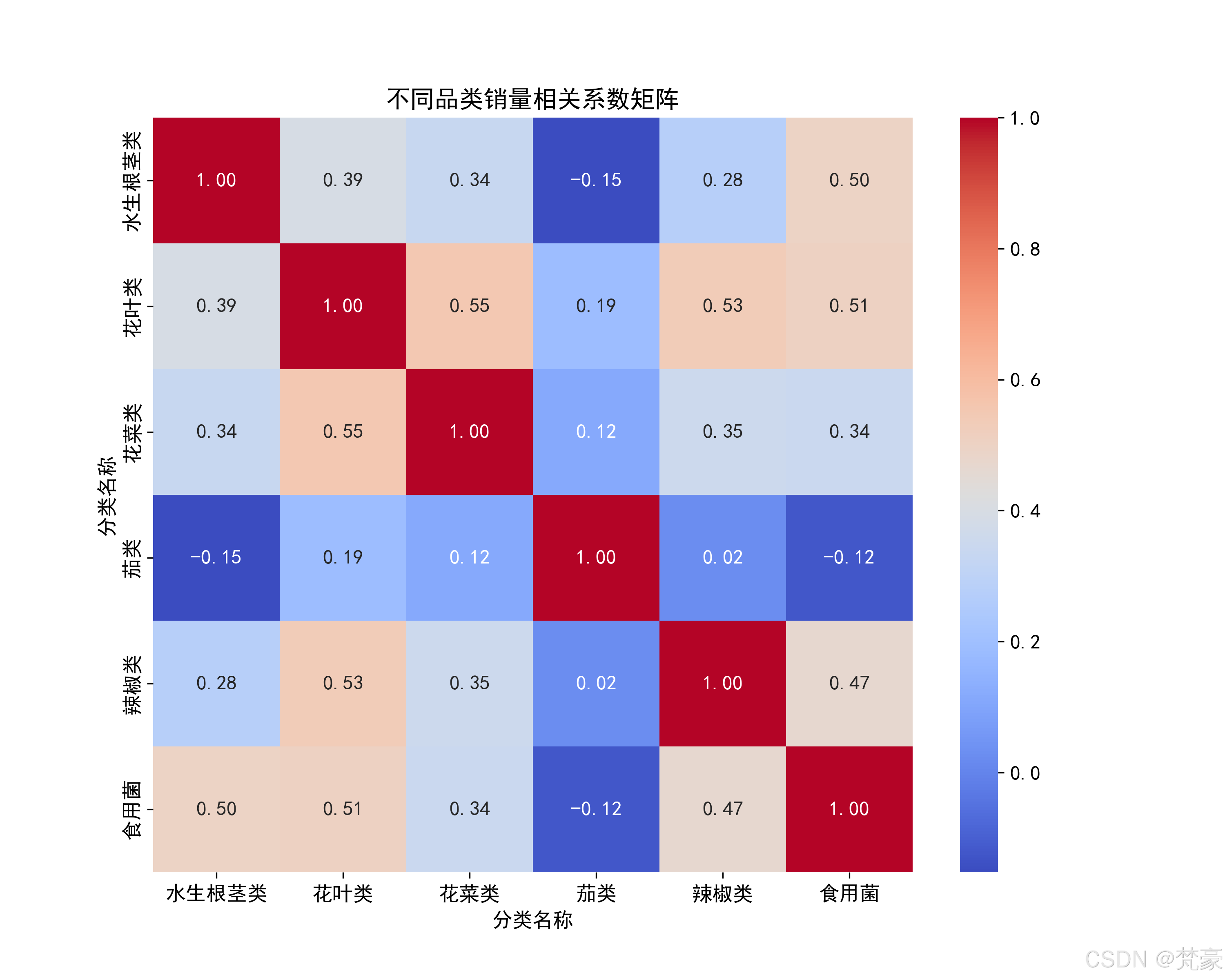
correlation_matrix = pivot_data.corr()plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', fmt=".2f")
plt.title('不同品类销量相关系数矩阵')
plt.savefig('品类销量相关系数热力图.png', dpi=300)
plt.show()
单品分析
筛选主要单品
筛选总销量占比超过1%的主要单品:
# 筛选主要单品(总销量占比>1%)
total_sales = merged_data['销量(千克)'].sum()
product_sales = merged_data.groupby('单品编码')['销量(千克)'].sum().reset_index()
product_sales['占比'] = product_sales['销量(千克)'] / total_sales * 100# 筛选占比>1%的单品
major_products = product_sales[product_sales['占比'] > 1]['单品编码'].tolist()
major_products_data = merged_data[merged_data['单品编码'].isin(major_products)]
相关性分析和聚类分析
对主要单品进行相关性分析和聚类分析:
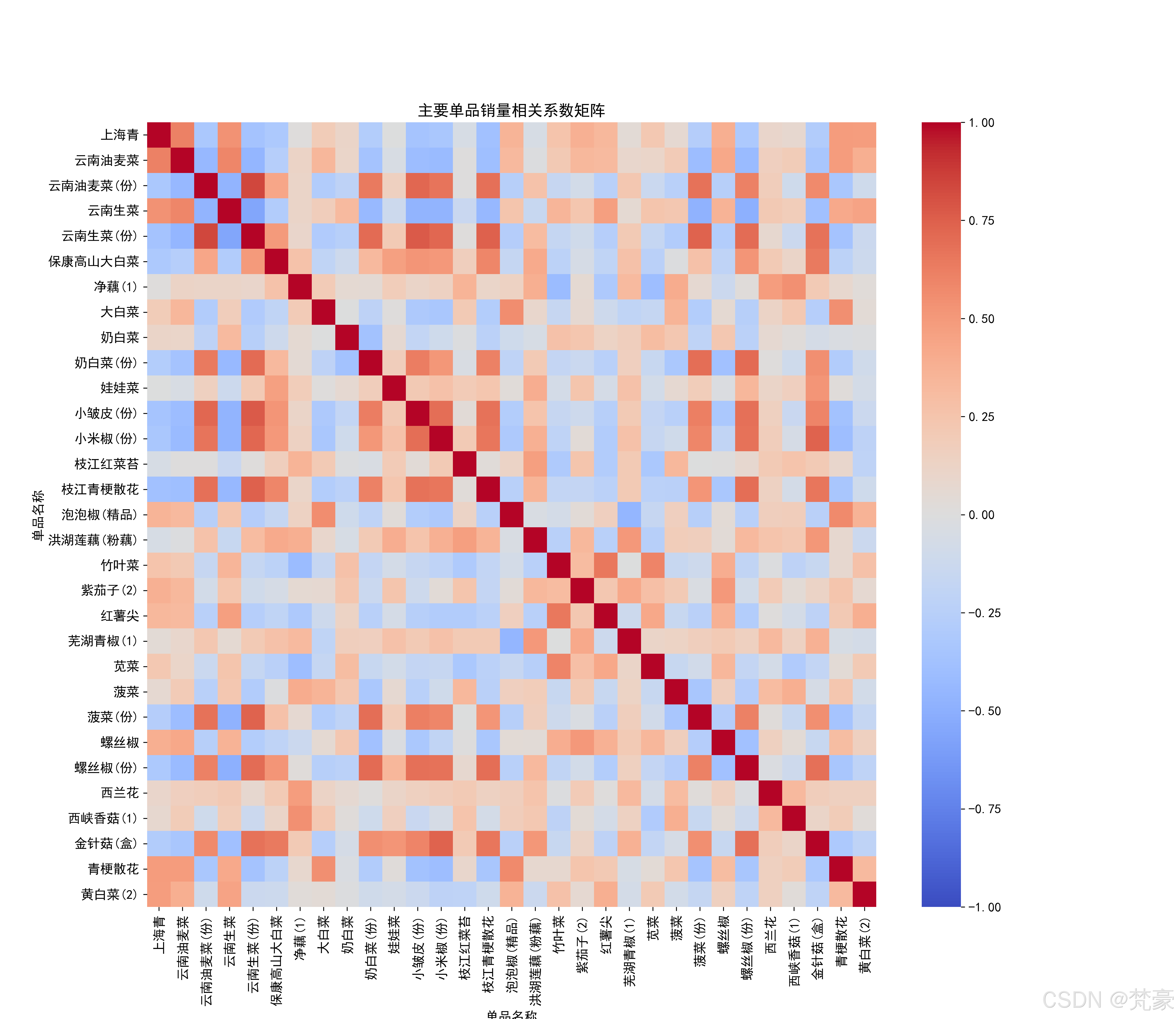
# 单品销量相关系数矩阵
product_pivot = major_products_data.pivot_table(index='日期', columns='单品名称', values='销量(千克)', aggfunc='sum'
).fillna(0)product_corr = product_pivot.corr()plt.figure(figsize=(15, 13))
sns.heatmap(product_corr, cmap='coolwarm', vmin=-1, vmax=1)
plt.title('主要单品销量相关系数矩阵')
plt.savefig('单品销量相关系数热力图.png', dpi=300)
plt.show()# 聚类分析准备
print(f"\n=== 聚类分析准备 ===")
print(f"主要单品数量: {len(major_products)}")
print(f"用于聚类的特征维度: {product_pivot.shape[1]}")
print(f"时间序列长度: {product_pivot.shape[0]}周")# 数据标准化
scaler = StandardScaler()
scaled_data = scaler.fit_transform(product_pivot.T)# 执行层次聚类
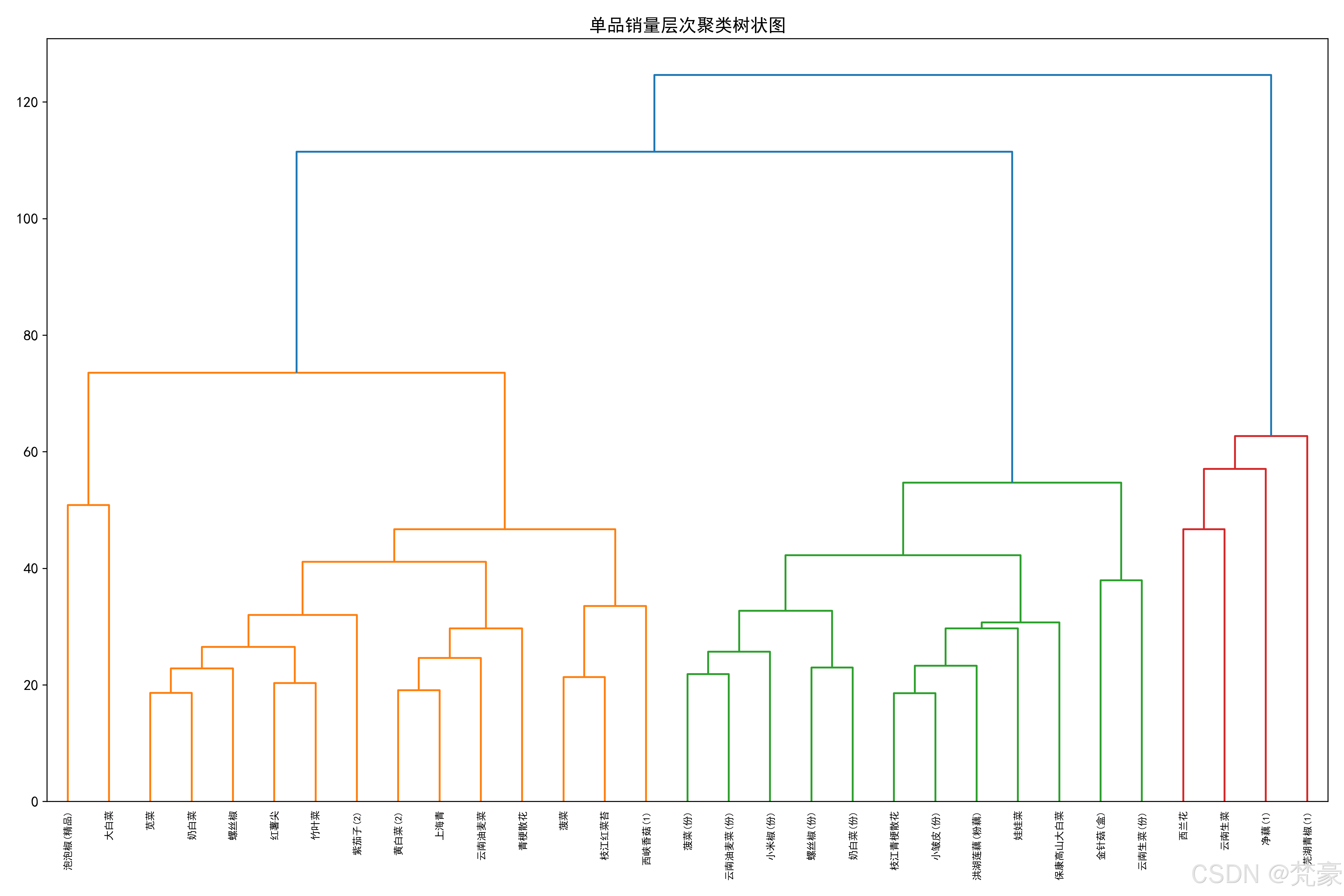
linked = linkage(scaled_data, 'ward')# 绘制树状图
plt.figure(figsize=(15, 10))
dendrogram(linked,orientation='top',labels=product_pivot.columns.tolist(),distance_sort='descending',show_leaf_counts=True)
plt.title('单品销量层次聚类树状图')
plt.xticks(rotation=90)
plt.tight_layout()
plt.savefig('单品销量层次聚类.png', dpi=300)
plt.show()
时间序列分析
对花叶类蔬菜进行时间序列分析和销量预测:
# 时间序列分析(以花叶类为例)
leafy_data = cleaned_category_data[cleaned_category_data['分类名称'] == '花叶类']
leafy_data = leafy_data.set_index('日期')['销量(千克)'].resample('W').sum()print(f"\n=== 花叶类蔬菜时间序列分析 ===")
print(f"原始周数据点数量: {len(leafy_data)}")
print(f"非零周数据点数量: {len(leafy_data[leafy_data > 0])}")
print(f"数据时间范围: {leafy_data.index.min()} 到 {leafy_data.index.max()}")# 数据预处理
leafy_data = leafy_data[leafy_data > 0] # 只保留有销售的周
leafy_data = leafy_data.dropna() # 去除NaN值print(f"预处理后数据点数量: {len(leafy_data)}")# 根据数据量选择合适的模型
data_points = len(leafy_data)
print(f"\n=== 模型选择 ===")
print(f"可用数据点数量: {data_points}")if data_points < 10:print("警告:花叶类蔬菜销售数据过少({}个数据点),无法进行有效的时间序列分析".format(data_points))print("建议:增加数据量或使用其他分析方法")
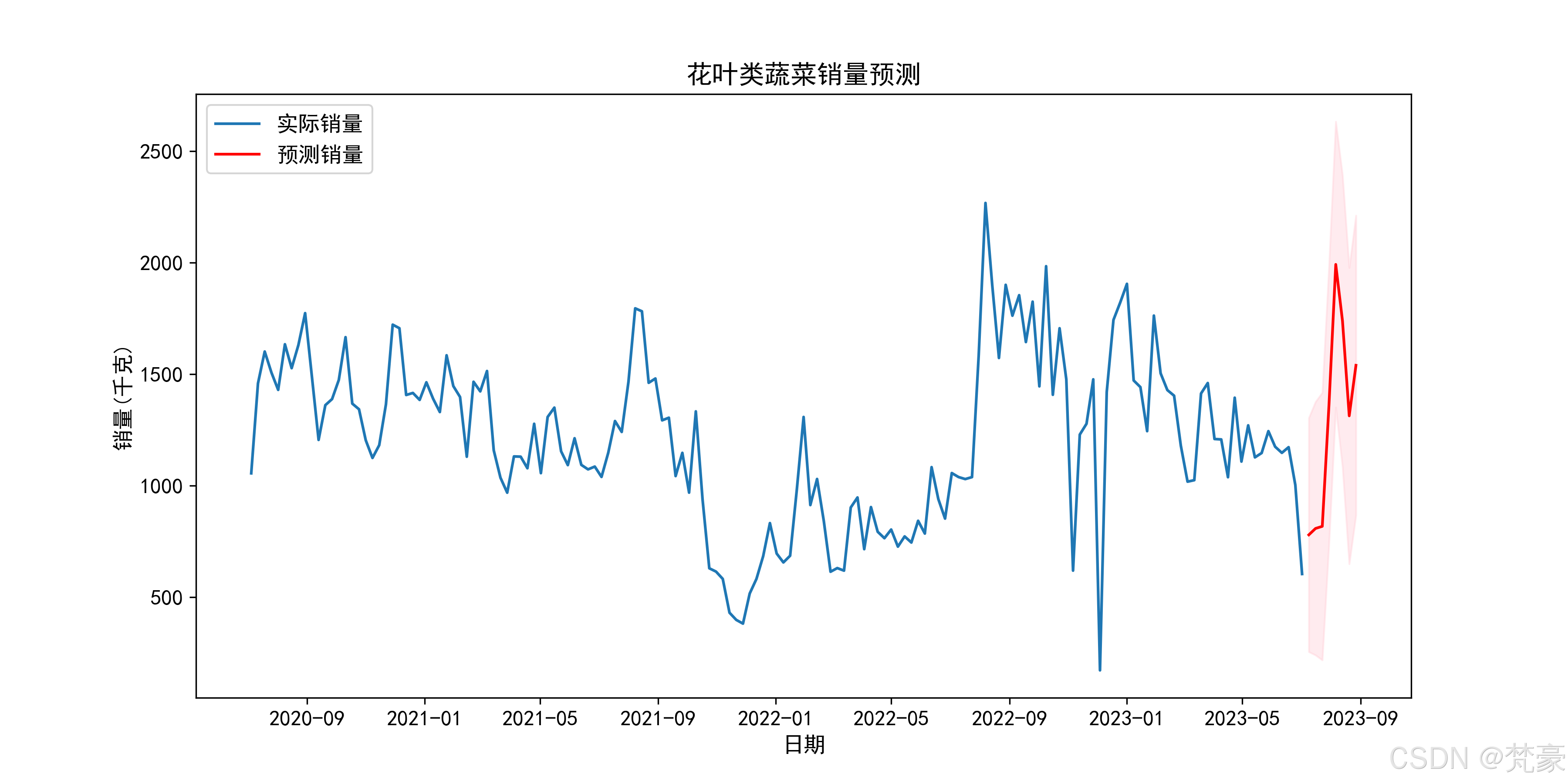
else:# 根据数据量选择模型if data_points < 20:print(f"数据量非常少({data_points}个数据点),使用简单ARIMA(1,1,1)模型")model = SARIMAX(leafy_data, order=(1, 1, 1), seasonal_order=(0, 0, 0, 0))elif data_points < 30:print(f"数据量较少({data_points}个数据点),使用ARIMA(1,1,1)模型")model = SARIMAX(leafy_data, order=(1, 1, 1), seasonal_order=(0, 0, 0, 0))elif data_points < 52:print(f"数据不足一年({data_points}个数据点),使用季度季节性模型")model = SARIMAX(leafy_data, order=(1, 1, 1), seasonal_order=(1, 1, 1, 13))else:print(f"数据充足({data_points}个数据点),使用年度季节性SARIMA模型")model = SARIMAX(leafy_data, order=(1, 0, 1), seasonal_order=(1, 1, 1, 52))try:# 模型拟合print("\n=== SARIMA模型拟合中 ===")results = model.fit(disp=True, maxiter=100)# 模型预测forecast = results.get_forecast(steps=8)forecast_mean = forecast.predicted_meanconf_int = forecast.conf_int()# 可视化预测结果plt.figure(figsize=(12, 6))plt.plot(leafy_data.index, leafy_data, label='实际销量')plt.plot(forecast_mean.index, forecast_mean, color='red', label='预测销量')plt.fill_between(conf_int.index,conf_int.iloc[:, 0],conf_int.iloc[:, 1],color='pink', alpha=0.3)plt.title('花叶类蔬菜销量预测')plt.xlabel('日期')plt.ylabel('销量(千克)')plt.legend()plt.savefig('花叶类销量预测.png', dpi=300)plt.show()print("时间序列分析完成,预测结果已保存为图表")except Exception as e:print(f"模型拟合过程中发生错误: {e}")print("时间序列分析无法完成")
代码运行结果如下:
“D:\Program Files\Python312\python.exe” D:\数学建模算法\2023年国赛C题\第一问.py
=== 数据预统计 ===
商品分类数量: 6
单品数量: 251
销售记录条数: 878503
时间跨度: 2020-07-01 00:00:00 到 2023-06-30 00:00:00
处理异常值: 100%|██████████| 6/6 [00:00<00:00, 52.18it/s]=== 开始K-S检验 ===
需要进行两两比较的品类组合数: 15
K-S检验进度: 100%|██████████| 6/6 [00:00<00:00, 90.61it/s]
不同品类销量分布K-S检验结果:
品类1 品类2 统计量 p值
0 水生根茎类 花叶类 0.885714 0.000000e+00
1 水生根茎类 花菜类 0.164781 2.212289e-13
2 水生根茎类 茄类 0.343502 2.359957e-56
3 水生根茎类 辣椒类 0.545622 1.395713e-148
4 水生根茎类 食用菌 0.406452 1.570512e-80
5 花叶类 花菜类 0.929028 0.000000e+00
6 花叶类 茄类 0.986175 0.000000e+00
7 花叶类 辣椒类 0.672811 1.325062e-233
8 花叶类 食用菌 0.739171 1.312185e-288
9 花菜类 茄类 0.446559 2.681445e-96
10 花菜类 辣椒类 0.574005 1.013998e-165
11 花菜类 食用菌 0.403415 1.990661e-79
12 茄类 辣椒类 0.840092 0.000000e+00
13 茄类 食用菌 0.723134 2.167953e-270
14 辣椒类 食用菌 0.211060 1.450780e-21=== 聚类分析准备 ===
主要单品数量: 31
用于聚类的特征维度: 31
时间序列长度: 1085周
D:\Program Files\Python312\Lib\site-packages\statsmodels\tsa\statespace\sarimax.py:866: UserWarning: Too few observations to estimate starting parameters for seasonal ARMA. All parameters except for variances will be set to zeros.
warn(‘Too few observations to estimate starting parameters%s.’=== 花叶类蔬菜时间序列分析 ===
原始周数据点数量: 157
非零周数据点数量: 157
数据时间范围: 2020-07-05 00:00:00 到 2023-07-02 00:00:00
预处理后数据点数量: 157=== 模型选择 ===
可用数据点数量: 157
数据充足(157个数据点),使用年度季节性SARIMA模型=== SARIMA模型拟合中 ===
RUNNING THE L-BFGS-B CODE* * *Machine precision = 2.220D-16
N = 5 M = 10At X0 0 variables are exactly at the bounds
At iterate 0 f= 4.74845D+00 |proj g|= 8.44600D-02
This problem is unconstrained.At iterate 1 f= 4.73793D+00 |proj g|= 3.47342D-02
At iterate 2 f= 4.73636D+00 |proj g|= 2.39635D-02
At iterate 3 f= 4.73446D+00 |proj g|= 9.59699D-03
At iterate 4 f= 4.73403D+00 |proj g|= 6.81549D-03
At iterate 5 f= 4.73191D+00 |proj g|= 1.90358D-02
At iterate 6 f= 4.73001D+00 |proj g|= 3.59550D-02
At iterate 7 f= 4.72664D+00 |proj g|= 2.41375D-02
At iterate 8 f= 4.72471D+00 |proj g|= 6.77773D-03
At iterate 9 f= 4.72459D+00 |proj g|= 7.50607D-03
At iterate 10 f= 4.72450D+00 |proj g|= 4.63116D-03
At iterate 11 f= 4.72441D+00 |proj g|= 1.93380D-03
At iterate 12 f= 4.72437D+00 |proj g|= 1.89523D-03
At iterate 13 f= 4.72430D+00 |proj g|= 2.94486D-03
At iterate 14 f= 4.72416D+00 |proj g|= 2.51350D-03
At iterate 15 f= 4.72408D+00 |proj g|= 1.54578D-03
At iterate 16 f= 4.72407D+00 |proj g|= 6.03074D-04
At iterate 17 f= 4.72407D+00 |proj g|= 3.17672D-04
At iterate 18 f= 4.72407D+00 |proj g|= 5.96141D-04
At iterate 19 f= 4.72405D+00 |proj g|= 2.08326D-03
At iterate 20 f= 4.72401D+00 |proj g|= 4.54286D-03
At iterate 21 f= 4.72389D+00 |proj g|= 8.46273D-03
At iterate 22 f= 4.72361D+00 |proj g|= 1.40379D-02
At iterate 23 f= 4.72286D+00 |proj g|= 1.97348D-02
At iterate 24 f= 4.72033D+00 |proj g|= 6.10411D-03
At iterate 25 f= 4.71943D+00 |proj g|= 1.22142D-02
At iterate 26 f= 4.71873D+00 |proj g|= 1.87391D-03
At iterate 27 f= 4.71865D+00 |proj g|= 2.29056D-03
At iterate 28 f= 4.71864D+00 |proj g|= 3.07135D-03
At iterate 29 f= 4.71863D+00 |proj g|= 2.90193D-03
At iterate 30 f= 4.71857D+00 |proj g|= 2.60038D-03
At iterate 31 f= 4.71839D+00 |proj g|= 3.56009D-03
At iterate 32 f= 4.71828D+00 |proj g|= 2.28461D-03
At iterate 33 f= 4.71820D+00 |proj g|= 2.56416D-03
At iterate 34 f= 4.71816D+00 |proj g|= 1.49224D-03
At iterate 35 f= 4.71811D+00 |proj g|= 2.10473D-03
At iterate 36 f= 4.71807D+00 |proj g|= 1.49416D-03
At iterate 37 f= 4.71805D+00 |proj g|= 1.29268D-03
At iterate 38 f= 4.71802D+00 |proj g|= 9.86987D-04
At iterate 39 f= 4.71801D+00 |proj g|= 1.41553D-03
At iterate 40 f= 4.71800D+00 |proj g|= 9.17988D-04
At iterate 41 f= 4.71798D+00 |proj g|= 1.22664D-03
At iterate 42 f= 4.71796D+00 |proj g|= 1.00516D-03
At iterate 43 f= 4.71795D+00 |proj g|= 1.97574D-04
At iterate 44 f= 4.71795D+00 |proj g|= 6.19423D-04
At iterate 45 f= 4.71794D+00 |proj g|= 5.49077D-04
At iterate 46 f= 4.71793D+00 |proj g|= 3.57586D-04
At iterate 47 f= 4.71792D+00 |proj g|= 2.70264D-04
At iterate 48 f= 4.71792D+00 |proj g|= 5.44453D-04
At iterate 49 f= 4.71792D+00 |proj g|= 3.17586D-04
At iterate 50 f= 4.71791D+00 |proj g|= 1.43407D-04
At iterate 51 f= 4.71791D+00 |proj g|= 1.16037D-03
At iterate 52 f= 4.71791D+00 |proj g|= 4.00691D-04
At iterate 53 f= 4.71791D+00 |proj g|= 2.21762D-04
At iterate 54 f= 4.71791D+00 |proj g|= 2.14908D-04
At iterate 55 f= 4.71791D+00 |proj g|= 3.06599D-04
At iterate 56 f= 4.71790D+00 |proj g|= 3.29918D-04
At iterate 57 f= 4.71790D+00 |proj g|= 2.10837D-04
At iterate 58 f= 4.71790D+00 |proj g|= 5.42502D-04
At iterate 59 f= 4.71790D+00 |proj g|= 1.89159D-04
At iterate 60 f= 4.71790D+00 |proj g|= 3.30017D-04
At iterate 61 f= 4.71790D+00 |proj g|= 8.11969D-05
At iterate 62 f= 4.71789D+00 |proj g|= 1.50932D-04
At iterate 63 f= 4.71789D+00 |proj g|= 3.61596D-04
At iterate 64 f= 4.71789D+00 |proj g|= 1.28840D-04
At iterate 65 f= 4.71789D+00 |proj g|= 1.38827D-04
At iterate 66 f= 4.71789D+00 |proj g|= 1.24965D-04
At iterate 67 f= 4.71789D+00 |proj g|= 2.07195D-04
At iterate 68 f= 4.71789D+00 |proj g|= 1.26451D-04
At iterate 69 f= 4.71789D+00 |proj g|= 9.24182D-05
At iterate 70 f= 4.71789D+00 |proj g|= 1.24965D-04
At iterate 71 f= 4.71789D+00 |proj g|= 3.78889D-04
At iterate 72 f= 4.71789D+00 |proj g|= 1.40783D-04
At iterate 73 f= 4.71789D+00 |proj g|= 8.27351D-05
At iterate 74 f= 4.71789D+00 |proj g|= 1.73230D-05
At iterate 75 f= 4.71789D+00 |proj g|= 8.21331D-05
At iterate 76 f= 4.71789D+00 |proj g|= 3.96216D-05
At iterate 77 f= 4.71789D+00 |proj g|= 1.73536D-04
At iterate 78 f= 4.71789D+00 |proj g|= 5.83873D-05
Bad direction in the line search;
refresh the lbfgs memory and restart the iteration.At iterate 79 f= 4.71789D+00 |proj g|= 3.32956D-05
* * *Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value* * *N Tit Tnf Tnint Skip Nact Projg F
5 79 115 2 0 0 3.330D-05 4.718D+00
F = 4.7178891464855557CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH
时间序列分析完成,预测结果已保存为图表进程已结束,退出代码为 0