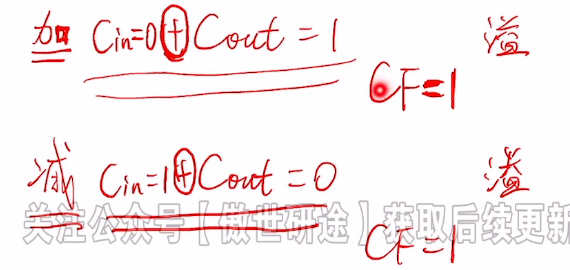移位运算以及定点数的加减法操作
首先介绍一下移位运算
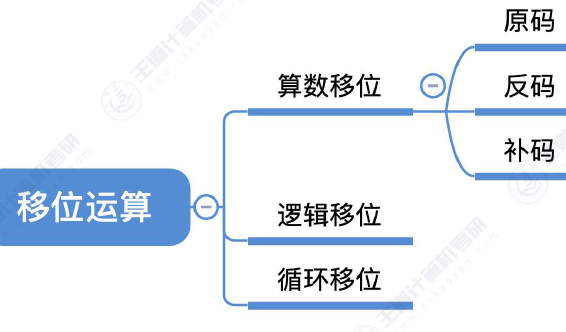
根据思维导图来看，分为算术移位、逻辑移位、循环移位三种
移位：通过改变各个数码位和小数点的相对位置，从而改变各数码位的位权。参照与十进制的移位（对于基数10来说）二进制的移位可用移位运算实现乘法、除法（对于基数2来说）。
算术移位
算术移位又分成了原码反码补码的移位因为他们的负数表示形式都不一样所以移位自然有着区别。
原码
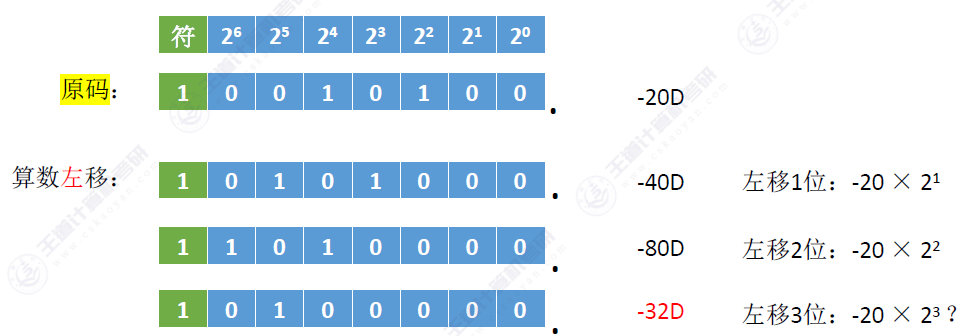
首先来看原码
移位时符号位不变改变的就只有数值位，
左移几位位权加几，移位为0时数值✖2，移位为1产生严重的误差。
右移时，右移几位位权降低几位，移位为0时相当于➗2。移位为1时丢失精度
对于小数来说道理相同，不过需要注意位权的问题。小数的位权
反码
接下来看反码的移位，前面说过反码只是一个中间态显得不是那么的重要。这里的移位运算也是同理，
注意一下反码的移位，对于正数来说原码、反码、补码的表示形式相同，这就使得他们的移位运算相同，对于负数来说反码对原码全部取反了，此时就需要在他的高位以及低位补1.这样做的目的是在将反码转换为原码求其数值为时1直接反为0使得转换出来的真值不会偏差太厉害
补码
接下里看一下补码，补码是由原码取反加一获得的。负数补码=反码末位+1导致反码最右边几个连续的1都因进位而变为0，直到进位碰到第一个0为止。
需要注意一下第一个一的位置。
记住左移加1，右移加0.
总计一下算术移位
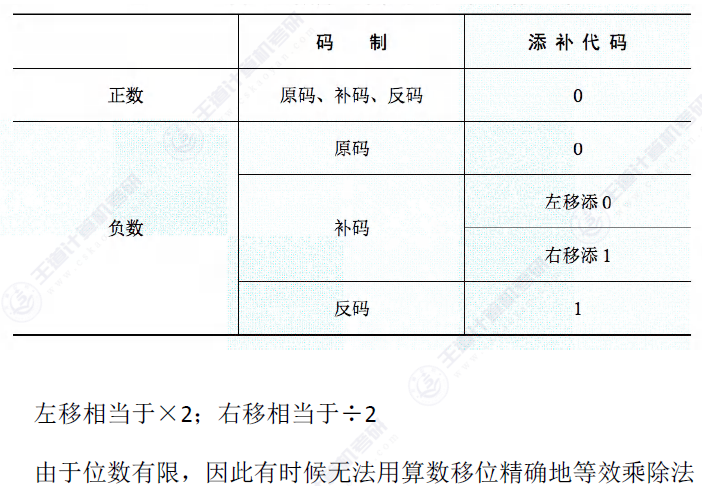
接下来我们看一个简单的算术移位
这里我们看到，可以对7进行拆解，同时呢用原来的数进行左右移的操作然后再相加就好，这就使得二进制的乘法可以转换为二进制的加法来处理。
逻辑移位
可以把逻辑移位看作是对“无符号数”的算数移位
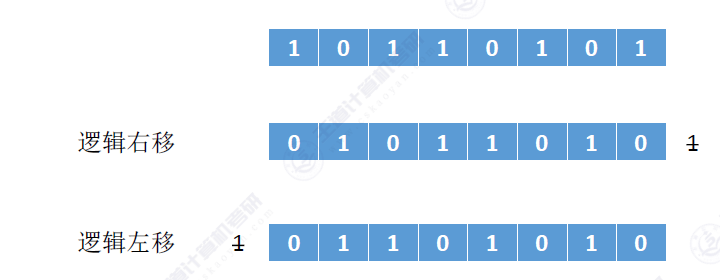
逻辑右移：高位补0，低位舍弃。
逻辑左移：低位补0，高位舍弃。
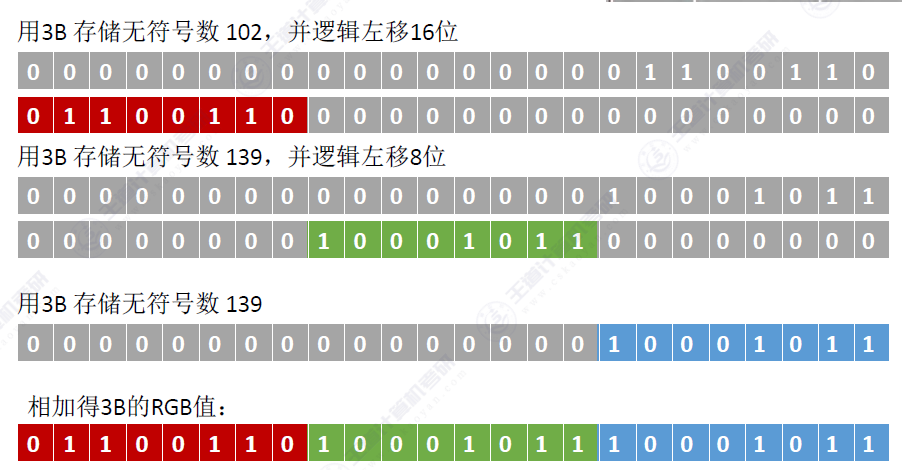
他的应用就简单了解一下可以组合数据的存储
循环移位
其实就是一个简单的循环末尾的元素添加到另外一段可以看成循环队列，最直观的理解就是跑马灯。
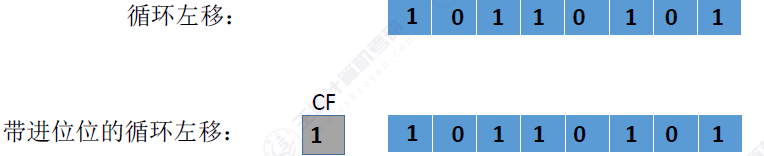
如果带进位位的话，直接带着进位位移动就好。
接下来看定点数的加减运算。
定点数的加减运算
注：计算机中，不会用“反码”进行加减运算，因此不作探讨
原码的加减法过于难不用太关注
首先简单介绍一下原码的加减法。
加法器直接对原码进行加法运算，可能出错。可能会上溢出也可能会下溢出。
原码的加法运算：
正+正à绝对值做加法，结果为正
负+负à绝对值做加法，结果为负
正+负à绝对值大的减绝对值小的，符号同绝对值大的数
负+正à绝对值大的减绝对值小的，符号同绝对值大的数
原码的减法运算，“减数”符号取反，转变为加法：
正-负à正+正
负-正à负+负
正-正à正+负
负-负à负+正
原码的剑法可以转换为剑法来运算，至于原码的加法产生溢出只会有两种情况；正+正；以及负+负
因为掐他的情况被中和了很难溢出。
至于溢出的处理可以参照接下来介绍的补码的溢出来操作。
接下来看一下补码的加减法运算。
补码加减法
对于补码的加减法来说，首先来加法，加法情况其实和原码一样需要注意一下溢出的问题
接下来是一个例题
对于补码的减法来说可以转换成加法来看待，由加法器实现运算，符号位也参与运算
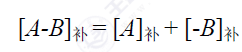
对于-B补来说，这里给出求法，先写出+B的补码找到+B补码从右到左的第一个1保持这个1不变剩下的左面全部取反（包括符号位）。
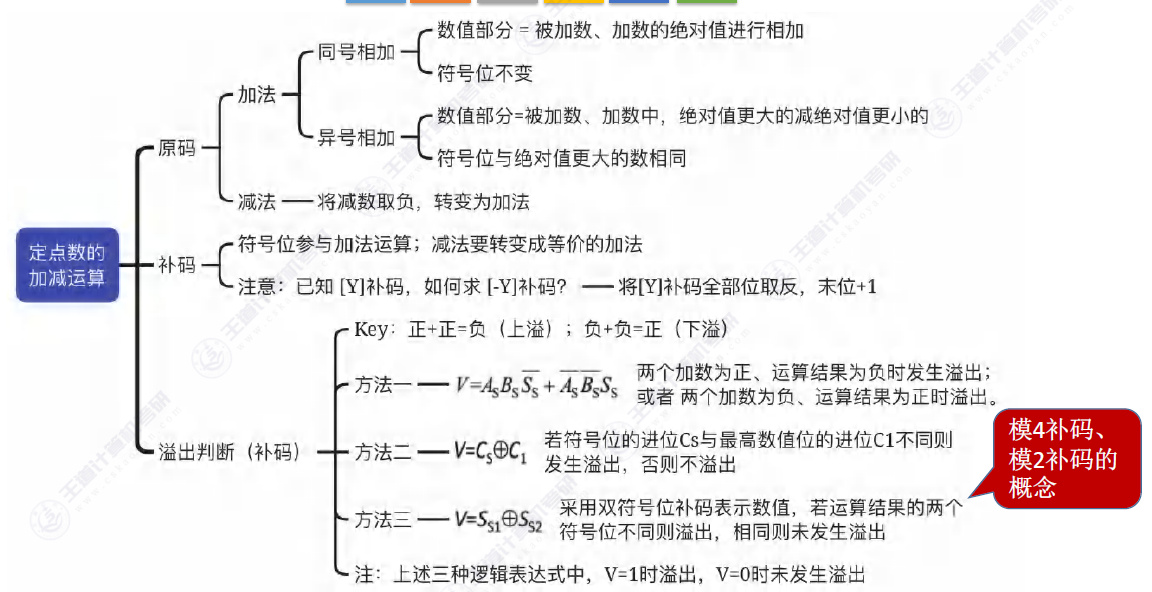
接下来介绍一下溢出的判断，前面说过正负或者负正的组合会抵消到一部分不会导致溢出，所以我们只需要关注到正正，和负负的组合。
先看一个溢出的例子
看方法的处理，首先看第一种方法（单符号位）
采用逻辑电路来判断，首先介绍一下逻辑表达式
采用到了多路的与门以及或门和非门，
首先看第一部分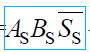
只有正正负负才来讨论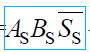当AB为1时同时对于结果来说S=0经过非门s=1此时对于多路与门来说结果为1同时对于大的或门来说结果一定为1，这是负负的情况下溢出
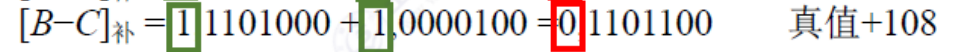
接下来我们看正正的溢出，我们看右面的部分
当AB=0时经过非门AB=1同时S=1时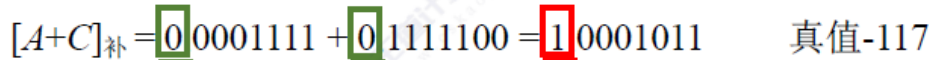
产生了溢出
接着看第二种办法，也是单符号位的判别方法
同时也是上一个例子
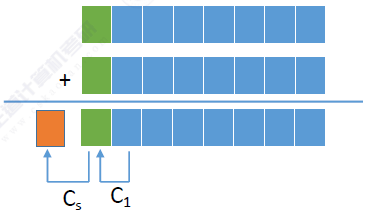
这里的主要思想是看数值位的进位以及符号位的进位。
即：CS与C1不同时有溢出
处理“不同”的逻辑符号：异或Å
溢出逻辑判断表达式为V=CSÅC1
若V=0，表示无溢出；V=1，表示有溢出。
正正上溢出
负负下溢出以及-补码的求法
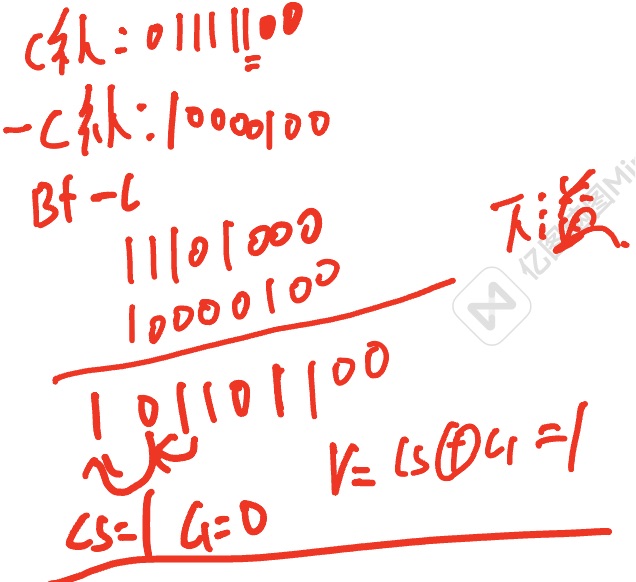
接着看第三种方法
第三种是双符号位的方法
说是双符号位，其实在存储的时候还是但符号位存储只是在运算的时候复制了一个符号位而已，但是要注意ALU处理的位数的问题，由于ALU处理的位数固定那么针对于双符号位的存储来说范围肯定就要比但符号位的范围小，因为他牺牲了一个符号位。
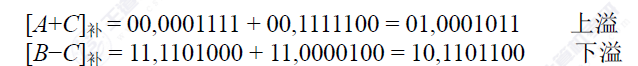
记两个符号位为SS1SS2，则V=SS1异或SS2
若V=0，表示无溢出；若V=1，表示有溢出。
双符号位补码又称：模4补码
单符号位补码又称：模2补码
无符号数的加减运算
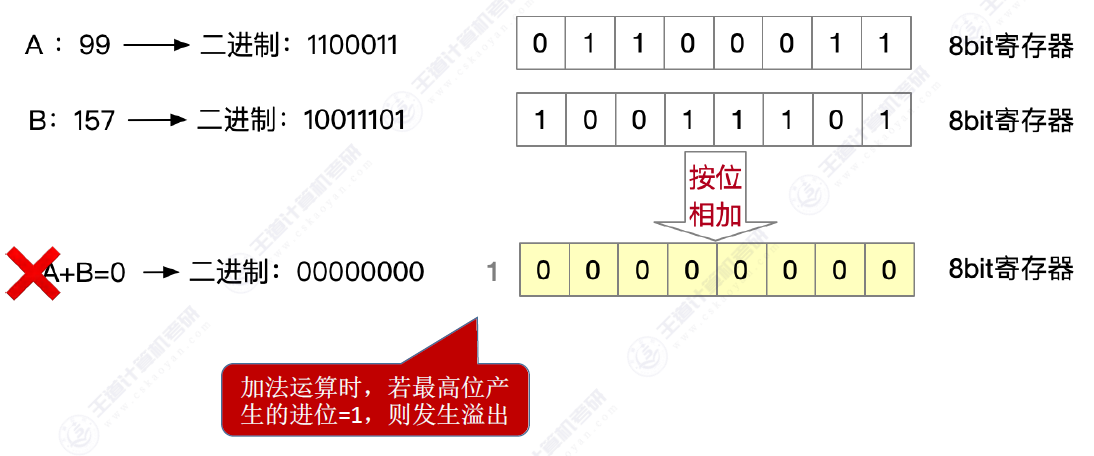
对于无符号数的加减运算来说
加法就是按位相加就好，
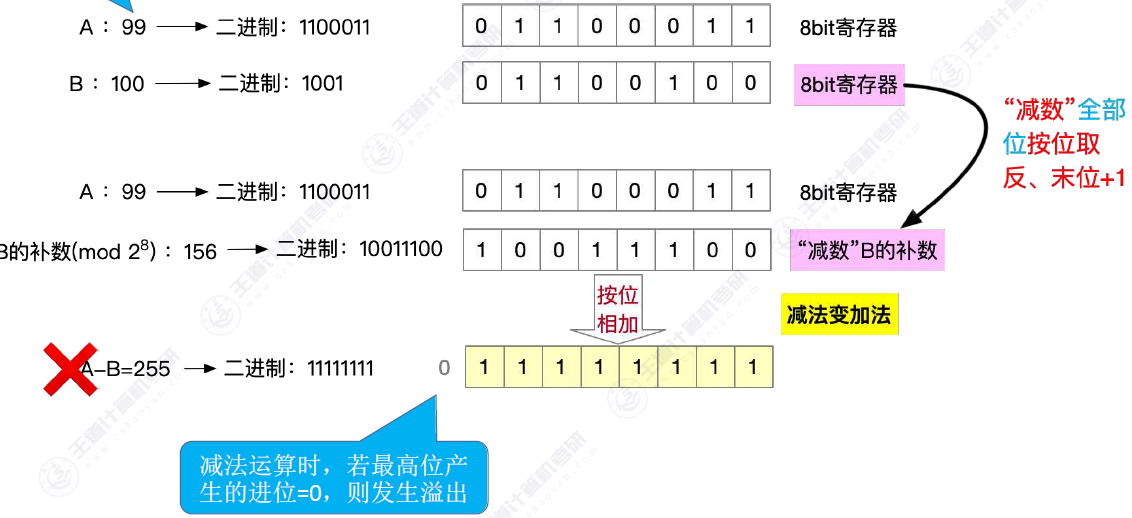
减法来说
其实简单点来说就和补码的减法差不多但是对于无符号数来说就不是求-补码了，对于无符号数来说是求补数（补数这个概念来说属于数论的范围，不需要太过于理解只需要知道他的求法就好了）补数的求法其实和-补码一样。
从右往左数第一个1不变左面的数全部取反（包括了符号位）然后就可以转换为加法来运算了
无符号的溢出判断
加法的溢出
减法的溢出，减法先转换为加法，然后逐位相加。
接下来看最重要的补码加减法运算电路
补码加减法运算电路。
首先回顾一下加法器（封装过后的）
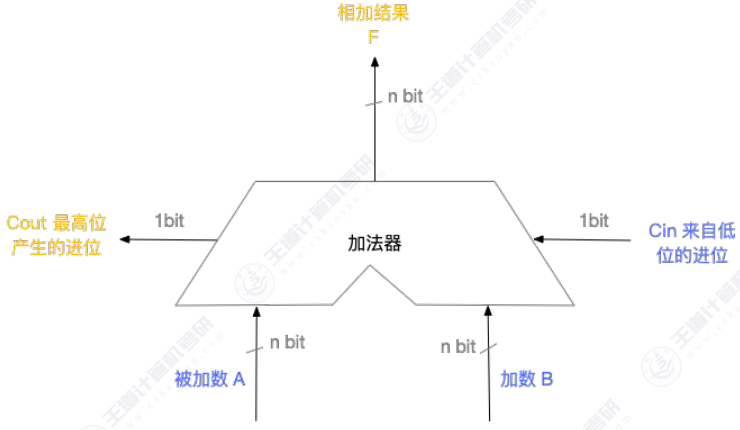
基于这个加法器电路多加一个多路选择器就可以的得到补码的加减法运算电路。
注意；这里输入的两个值都是补码的形式。
接下来讲解一下这个电路，加入了一个多路选择器。这里低位的进位不需要关注。
可以看到当时加法的时候多路选择器控制信号位0同时给到低位仅为的值也为0 .此时加法就只需要按位相加就好了。
接着看一下减法减法的控制信号是1选择一时经过多路选择器补码被全部取反了，同时进位信号位1.这时候cin=1此时补码减法变加法的操作就实现了，求负补码的操作是全部位取反加一多路选择器实现了取反的操作，cin实现了+1的操作。
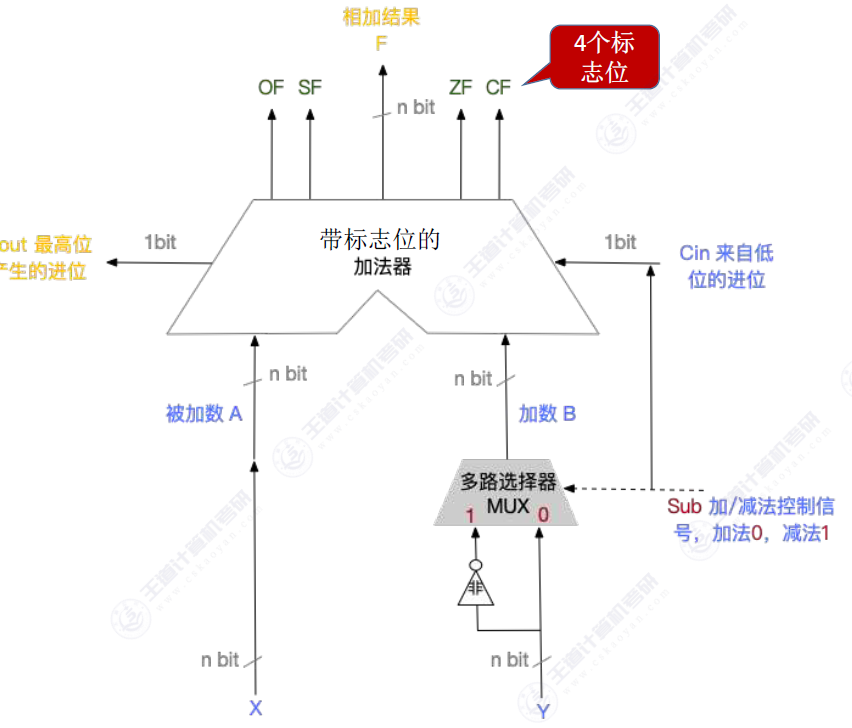
SF解释过了。直接选择加法器的最高位看看是否位负
ZF 其实就是采用了一个或非门。
接下来解释一下
OF
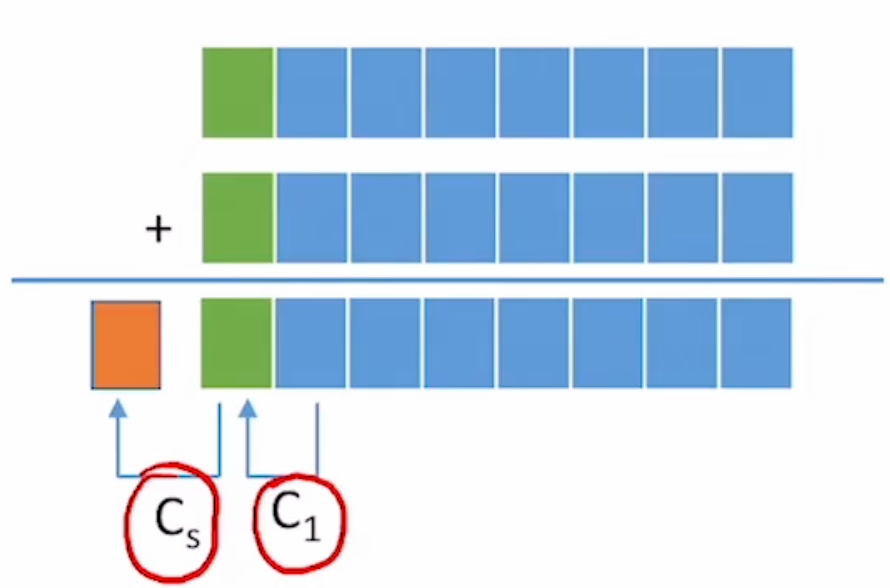
注意一下这里的最高位和次高位
OF = Cn⊕Cn-1 ——即最高位的进位Å次高位的进位。反映带符号数加减运算是否溢出。
CF
无符号数的溢出判断
结合一下补码电路的多路选择器得出cin
