子数组和 问题汇总
文章目录
- 买卖股票的最佳时机
- 最大子数组和
- 拓展
- 如果求解的是需要返回具体的数组(或者下标)
- 如果子数组长度有下界
- 如果子数组长度存在上界
- 子数组的长度固定求解窗口最大值
- 长度小总结
- 子数组的长度必须是奇数
子数组:也就是在原来的数组当中连续的元素,那么对应的解题方法也是有套路的:常用思路:使用前缀和+贪心、动态规划(例如,dp[i]为以nums[i]结尾的最值情况)限制子数组的长度:使用窗口窗口内最值:使用单调队列
买卖股票的最佳时机
买卖股票的最佳时机
思路分析:贪心:最大的利益收益,那么对于某一天i来说,我们只需在它前面的那么多天当中,价格最低的哪一天买入,也就是维护一个变量leftmin,我们就可以计算出当天i卖出的可以赚到的最优情况,将nums[i] - leftmin与我们的答案ans进行比较,然后进行更新(插播一句,所谓的优化,也只是优化这个遍历的情况的时间复杂度,减少无效多余的情况)
class Solution {
public:int maxProfit(vector<int>& prices) {// 贪心问题int n = prices.size(),leftmin = prices[0],ans = 0;for (int i = 1;i < n; i++){int tmp = prices[i] - leftmin;ans = tmp > ans ? tmp : ans;leftmin = min(leftmin,prices[i]);}return ans;}
};
最大子数组和
思路分析:前缀和+贪心: 涉及到子数组和的问题,当我们求解出nums数组的前缀和的时候,就可以转化为上面的买卖股票的最佳时机的问题动态规划:我们规定dp[i]为以nums[i]结尾的最大子数组的和,就有递推公式dp[i] = max(dp[i-1]+nums[i],nums[i])
前缀和+贪心:
class Solution {
public:int maxSubArray(vector<int>& nums) {// 最大子数组和 // 涉及到这个的都一般使用前缀和,然后使用贪心的买卖股票的思路int n = nums.size();vector<int> pre(n+1);for (int i = 0; i < n; i++){pre[i+1] = pre[i] + nums[i];}// 开始贪心int leftmin = 0,ans = -0x3f3f3f3f;for (int i = 0;i < n;i++){ans = max(ans,pre[i+1] - leftmin);leftmin = min(leftmin,pre[i+1]);}return ans;}
};
动态规划:
class Solution {
public:int maxSubArray(vector<int>& nums) {// 最大子数组和 // 使用动态规划// dp[i]为以nums[i]结尾的最大子数组和int n = nums.size();vector<int> dp(n);dp[0] = nums[0];int ans = dp[0];for (int i = 1; i < n; i++){dp[i] = max(nums[i],dp[i-1] + nums[i]);ans = max(ans,dp[i]);}return ans;}
};
拓展
如果求解的是需要返回具体的数组(或者下标)
思路分析:对于这种需要返回具体的数组的情况,当然得使用left、right、ansleft、ansright4个变量进行分别记录 当前情况的子数组的两端和最右情况的两端更新策略:(使用动态规划思路):当dp[i-1] + nums[i] > nums[i]的时候,有更新right = i,不用更新这个left;否则就是更新left = i,right = i。当最终的dp[i]>ans的时候,我们才有更新ansleft = left,ansright = right
class Solution {
public:int maxSubArray(vector<int>& nums) {// 如果需要返回这个子数组,那其实只要记录这个子数组的两个端点即可int n = nums.size(),left = 0,right = 0,ansleft = 0,ansright = 0;// 使用动态规划求解vector<int> dp(n);dp[0] = nums[0];int ans = dp[0];for (int i = 1;i < n ;i++){if (dp[i-1] + nums[i] > nums[i]){right = i;}else{left = i;right = i;}dp[i] = max(dp[i-1] + nums[i],nums[i]);if (dp[i] > ans){ansleft = left;ansright = right;}ans = max(ans,dp[i]);}cout << ansleft << " " << ansright ;return ans;}
};
如果子数组长度有下界
-
题目要求:求解原数组当中,子数组的和的最大值,要求子数组的长度必须>=k -
思路分析:滑动窗口:对于长度的限制,就是要设置一个窗口来实现,但是对于窗口内的最小值的选取,就需要使用到这个单调队列,优先队列的话,我们在加入新元素的时候,会把队列当中比它大的元素全部出队列,最终就可以实现,队列的元素是逐渐递增的,q.front是窗口最小的元素
class Solution {
public:int maxSubArray(vector<int>& nums) {// 如果求解的是有下界的最大子数组和的问题int n = nums.size();vector<int> pre(n+1);for (int i = 0;i < n;i++){pre[i+1] = pre[i] + nums[i];}int ans = -0x3f3f3f3f,leftmin = 0;// 使用优先队列,保持一个递增的队列deque<int> q;for (int i = k; i <= n;i++){int left = i - k;// 将左端点放进去while ( !q.empty() && pre[q.back()] > pre[left]){q.pop_back();}q.push_back(left);// 更新答案if (!q.empty()){ans = max(ans, pre[i] - pre[q.front()]);}}return ans;}
};
如果子数组长度存在上界
-
问题要求:求解原数组当中,求解最大子数组和,并且要求子数组的长度必须<=k -
思路分析:确保窗口的最大值<=k:我们对于这个单调队列q.front<left就弹出(队列当中的值存储的是下标,并且下标是递增的)即可,就是在这个下界基础上,增加了对这个队列首部元素的判断
class Solution {
public:int maxSubArray(vector<int>& nums) {// 如果求解的是有上界的最大子数组和的问题int n = nums.size();vector<int> pre(n+1);for (int i = 0;i < n;i++){pre[i+1] = pre[i] + nums[i];}int ans = -0x3f3f3f3f,leftmin = 0;// 使用优先队列,保持一个递增的队列deque<int> q;for (int i = k; i <= n;i++){int left = i - k;while (!q.empty() && q.front < left){q.pop_front();}// 将左端点放进去while ( !q.empty() && pre[q.back()] > pre[left]){q.pop_back();}q.push_back(left);// 更新答案if (!q.empty()){ans = max(ans, pre[i] - pre[q.front()]);}}return ans;}
};
子数组的长度固定求解窗口最大值
滑动窗口最大值
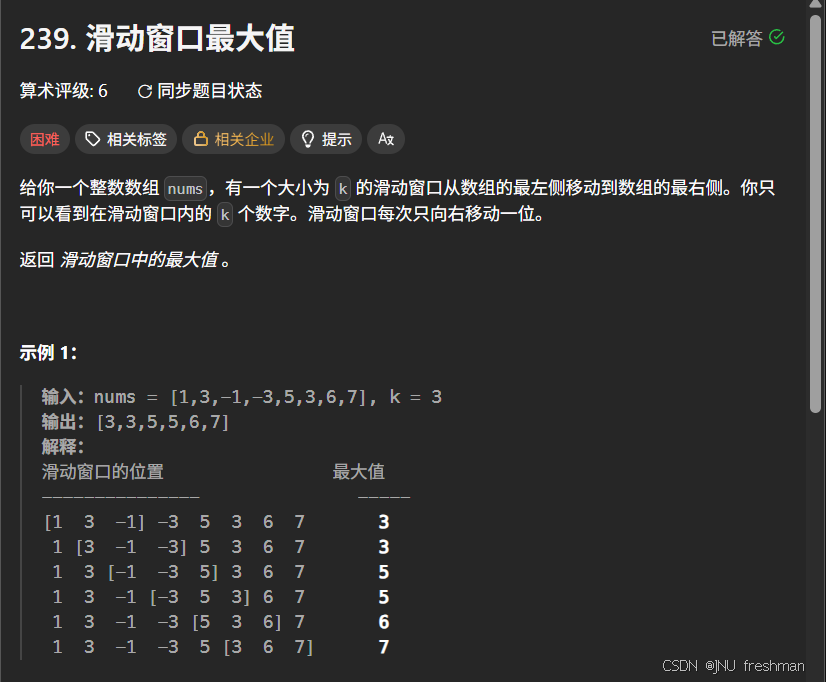
思路分析:固定长度的区别:由于要保持这个单调性问题,所以在队列的末尾增加这个元素的时候,使用的是while也就是不满足的元素都会出队列,但是由于要保证这个子数组的长度是k,所以每次出队列只用出一个元素,所以使用的是if
class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {vector<int> ans;int n = nums.size();// 使用一个双端队列来实现,保证每一个元素只进来一次deque<int> q;for (int i = 0; i < n;i++){// 右边进入while (!q.empty() && nums[q.back()] <= nums[i]){q.pop_back();}q.push_back(i);// 左边出int left = i - k + 1;if (q.front() < left){q.pop_front();}// 在窗口左端点记录答案if (left >=0 ){ans.push_back(nums[q.front()]);}}return ans;}
};长度小总结
一般思路:出队列,入队列,更新细节区别:入队列是必须的,出队列不一定(子数组有下界要求不用出队列);出队列的次数不一定(固定长度每次出一个即可)
子数组的长度必须是奇数
题目要求:要求求解的子数组的最大和的同时这个子数组的长度必须是奇数思路分析:由于要求长度必须是奇数,也就是需要记录奇数和偶数的情况,所以我们采用动态规划的思想:dp0[i]表示以nums[i]结尾的偶数长度的子数组的最大和dp1[i]表示以nums[i]结尾的奇数长度的子数组的最大和- 递推公式
dp0[i] = dp1[i-1] + nums[i]和dp1[i] = max(dp0[i-1] + nums[i],nums[i])
class Solution {
public:int maxSubArray(vector<int>& nums) {// 如果求解的是长度必须是奇数的最大子数组和的问题int n = nums.size();// 使用动态规划// dp0[i]表示以nums[i]结尾长度为偶数的最大子数组和// dp1[i]表示以nums[i]结尾长度为奇数的最大子数组和vector<int> dp0(n),dp1(n);dp0[0] = -0x3f3f3f3f;dp1[0] = nums[0];int ans = dp1[0];for (int i = 1;i < n;i++){dp0[i] = dp1[i-1] + nums[i];dp1[i] = max(dp0[i-1] + nums[i],nums[i]);ans = max(ans,dp1[i]);}return ans;}
};
