机器学习笔记(四)——聚类算法KNN、Kmeans、Dbscan
写在前面:
写本系列(自用)的目的是回顾已经学过的知识、记录新学习的知识或是记录心得理解,方便自己以后快速复习,减少遗忘。概念部分大部分来自于机器学习菜鸟教程,公式部分也会参考机器学习书籍、阿里云天池。机器学习如果只啃概念始终学不牢,因此我打算概念与代码结合。
Part 2 机器学习算法
五、KNN
1、KNN的基本原理
KNN,也叫K近邻算法,是一种简单且常用的分类和回归算法。它是监督学习的一种,核心思想是通过计算待分类样本与训练集中各个样本的距离,找到距离最近的 K 个样本,然后根据这 K 个样本的类别或值来预测待分类样本的类别或值。
现在举一个例子,示例中的图片来自b站up小萌Annie的K近邻算法视频:
假设有两种狼群,狼群A和狼群B。其中,狼群A的脚印用图中绿色的圆圈来表示,狼群B的脚印用图中绿色的正方形来表示。现在给出一个不知道类别的脚印(图中黑色爪印),问这个脚印是狼群A留下的还是狼群B留下的。解决这个问题可以使用KNN算法。
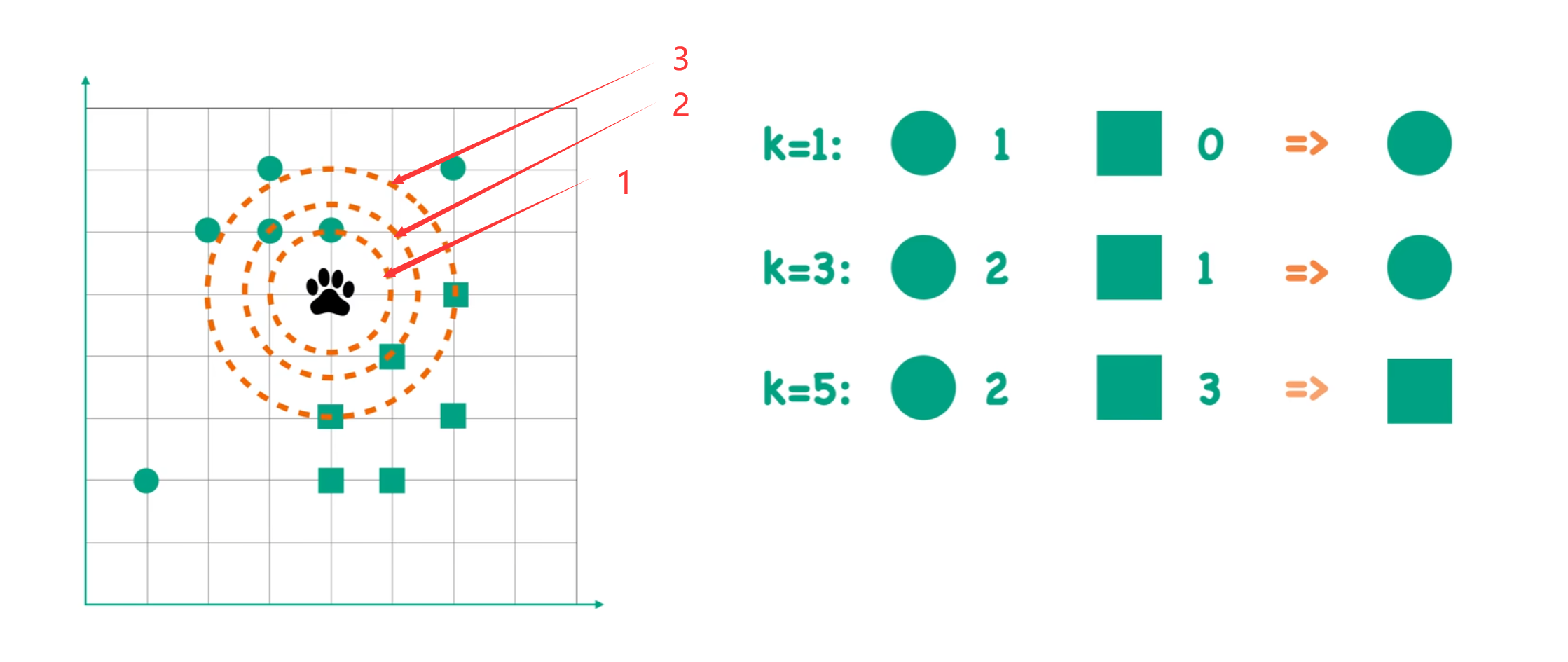
假设我们设置KNN的距离超参数k = 1。也就是说,以待分类样本(黑色爪印)为圆心,k=1为半径画圆,看圆内哪种脚印数量多。例如图中,当k = 1时,圆圈的数量为1,方形的数量为0,因此我们判断黑色脚印是圆形,即待分类样本属于狼群A。
同理,k = 3时,圆圈的数量为2,方形的数量为1,因此我们判断黑色脚印是圆形,即待分类样本属于狼群A。
k = 5时,圆圈的数量为2,方形的数量为3,因此我们判断黑色脚印是方形,即待分类样本属于狼群B。
这就是KNN算法解决分类问题的案例(解决回归问题就是取k个最近邻点的平均值)。那么需要解决的问题就是KNN算法的距离如何度量。
2、距离度量(可以只了解欧氏距离)
这里shun'dai常用的距离度量方法如下:
(1)欧式距离
欧式距离是KNN最常用的距离度量,计算n维空间中两点x、y的直线距离的公式为:
(2)曼哈顿距离
计算n维空间中两点在网格状空间中的最短路径距离,如城市街区距离:
(3)切比雪夫距离
表示两点在各维度上差值的最大值:
(4)闵可夫斯基距离
是欧氏距离和曼哈顿距离的广义形式:
当p=1时为曼哈顿距离,p=2时是欧式距离,p趋于无穷时等价于切比雪夫距离。
(5)余弦相似度
衡量两个n维向量方向的相似性:
这里,分子是两个向量x、y的点积;分母是向量模长的乘积。
(6)汉明距离
两个等长字符串对应位置不同字符的数量,常用于分类变量:
d(x, y) = 不同位置的数量
(7)马氏距离
考虑数据分布协方差的距离度量,消除特征间的相关性:
其中,S是数据的协方差矩阵。
(8)编辑距离
将一个字符串转换为另一个字符串所需的最少编辑操作次数(插入、删除、替换)。
在KNN中,距离度量的选择直接影响算法性能。不同距离函数会导致不同的近邻定义,从而影响结果,最常用的距离是欧氏距离。
例如,图像识别,地理坐标分析等常用欧氏距离;文本分类等常用余弦相似度;棋盘游戏可以考虑切比雪夫距离。如果难以抉择如何选取距离,可以通过交叉验证比较不同距离函数的性能。
3、KNN步骤总结
KNN算法的步骤可以概括如下:
1、计算距离:计算待分类样本与训练集中每个样本的距离。
2、选择k个最近邻样本。
3、投票或取平均:对于分类问题,K 个最近邻中出现次数最多的类别即为待分类样本的类别;对于回归问题,K 个最近邻的值的平均值即为待分类样本的值。
4、KNN的代码实现
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score# 加载Iris数据集
iris = datasets.load_iris()
X = iris.data # 只取前两个特征
y = iris.target# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)# 创建KNN模型,设置K值为3
knn = KNeighborsClassifier(n_neighbors=3)
'''
这里是默认使用欧氏距离,也就是:
knn = KNeighborsClassifier(n_neighbors=3, metric='euclidean')
metric就是选择距离度量方式,'euclidean'是欧式距离
'manhattan'是曼哈顿、'chebyshev'是切比雪夫、'cosine'是余弦、'hamming'是汉明、'mahalanobis'是马氏距离
metric='minkowski', p=2这样是参数为2的闵可夫斯基距离
当然,也可以自定义距离函数
写好函数后将函数传入,即 metric= 函数名 即可。
'''# 训练模型
knn.fit(X_train, y_train)# 在测试集上进行预测
y_pred = knn.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print(f"KNN模型的准确率: {accuracy:.4f}")六、k-means
1、k-means的原理
k-means算法也是一种经典的无监督学习算法。它的目标是:将n个数据点划分为k个簇,每个簇由其质心代表,使得所有数据点到其所属质心的平方和距离最小。
2、算法步骤
1、初始化:随机选取k个数据点作为初始的质心;
2、分配:将每个数据点分配到距离最近的质心所在的簇;(这里默认使用且最常使用的是欧式距离,也可以使用其他距离度量方式)
3、更新:重新计算每个簇的质心,质心的计算是对簇内所有数据点的每个维度取平均值。
例如某簇里有三个点:(1, 2),(3, 4),(5, 6),该簇的中心就是(3, 4)。=>((1+3+5)/3,(2+4+6)/3)
4、迭代:重复步骤 2-3,直到质心不再变化或达到最大迭代次数。
3、示例
示例来源于b站up平安喜悦孙瑜的k-means聚类算法讲解视频。
1、初始化三个质心:黄、蓝、绿
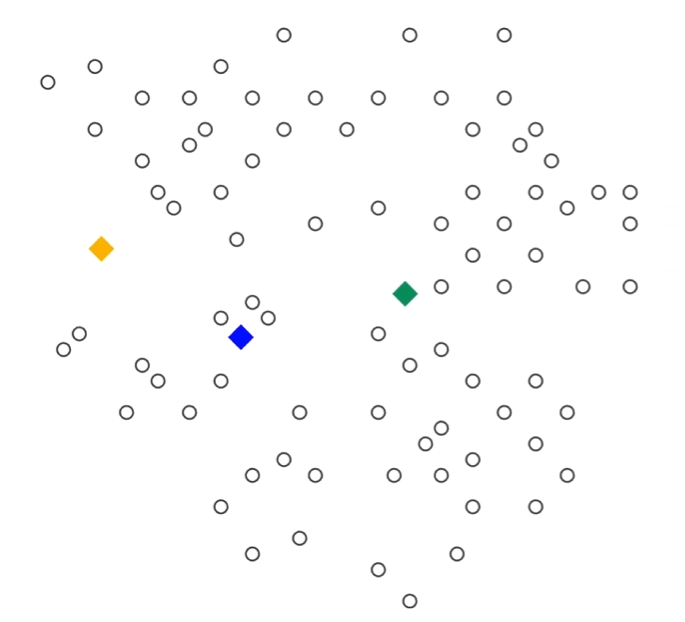
2、对每个白色的点,分别计算它到这三个质心的距离。离哪个质心近,就把它归为那一类。每个点均分类完成后如下图:
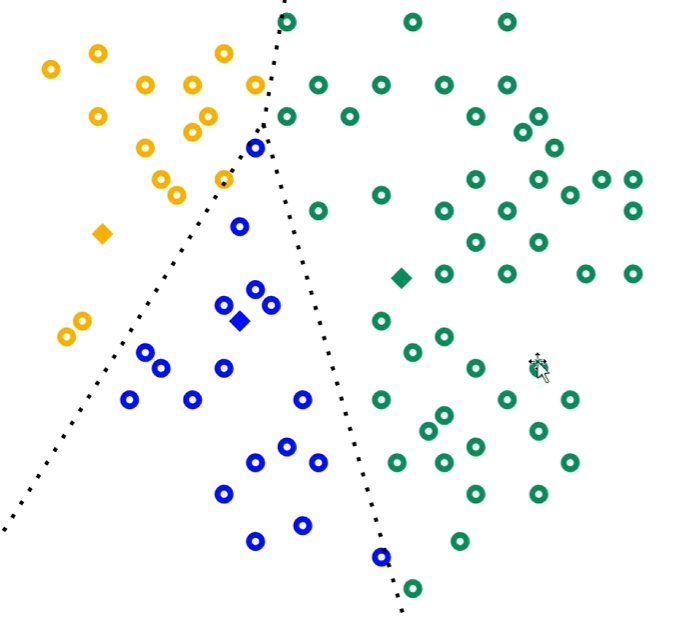
3、计算出三个类的质心,作为新的簇中心:
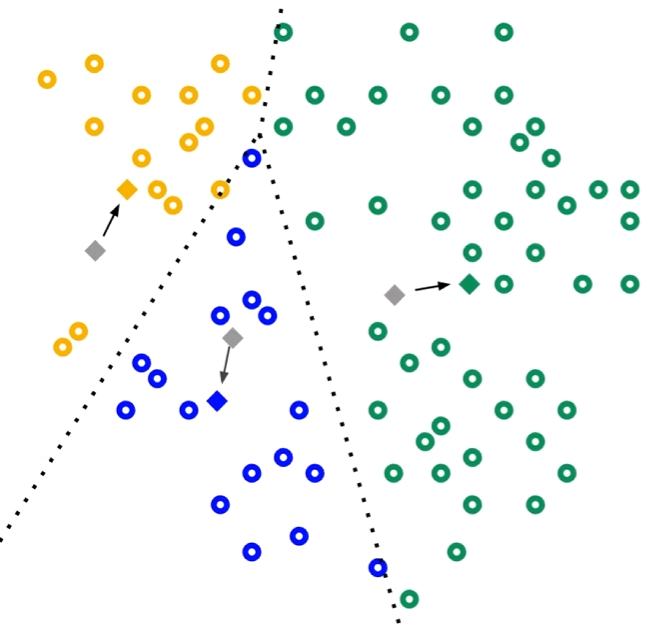
4、算出簇中心后,重新计算每个点离三个质心的距离,重新分类;一直循环直到质心不再变化或者达到最大迭代次数。
4、代码实现
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt# 生成模拟数据(3个簇)
X, _ = make_blobs(n_samples=300, centers=3, cluster_std=0.60, random_state=42)# 构建 K-means 模型
kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300, random_state=42)
y_pred = kmeans.fit_predict(X)# 可视化结果
plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap='viridis')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red', marker='X')
plt.title('K-means Clustering')
plt.show()七、DBSCAN
1、算法原理
DBSCAN是一种基于密度的空间聚类算法,能够将高密度区域划分为簇,并将低密度区域识别为噪声点。DBSCAN中有以下几个核心概念:
设有n个待聚类点,当前操作点设为p点。
1、ε 邻域:以点 p 为中心、半径为 ε 的区域。如下图所示,p点为中心, ε =2,黑色圆内即为ε 邻域。
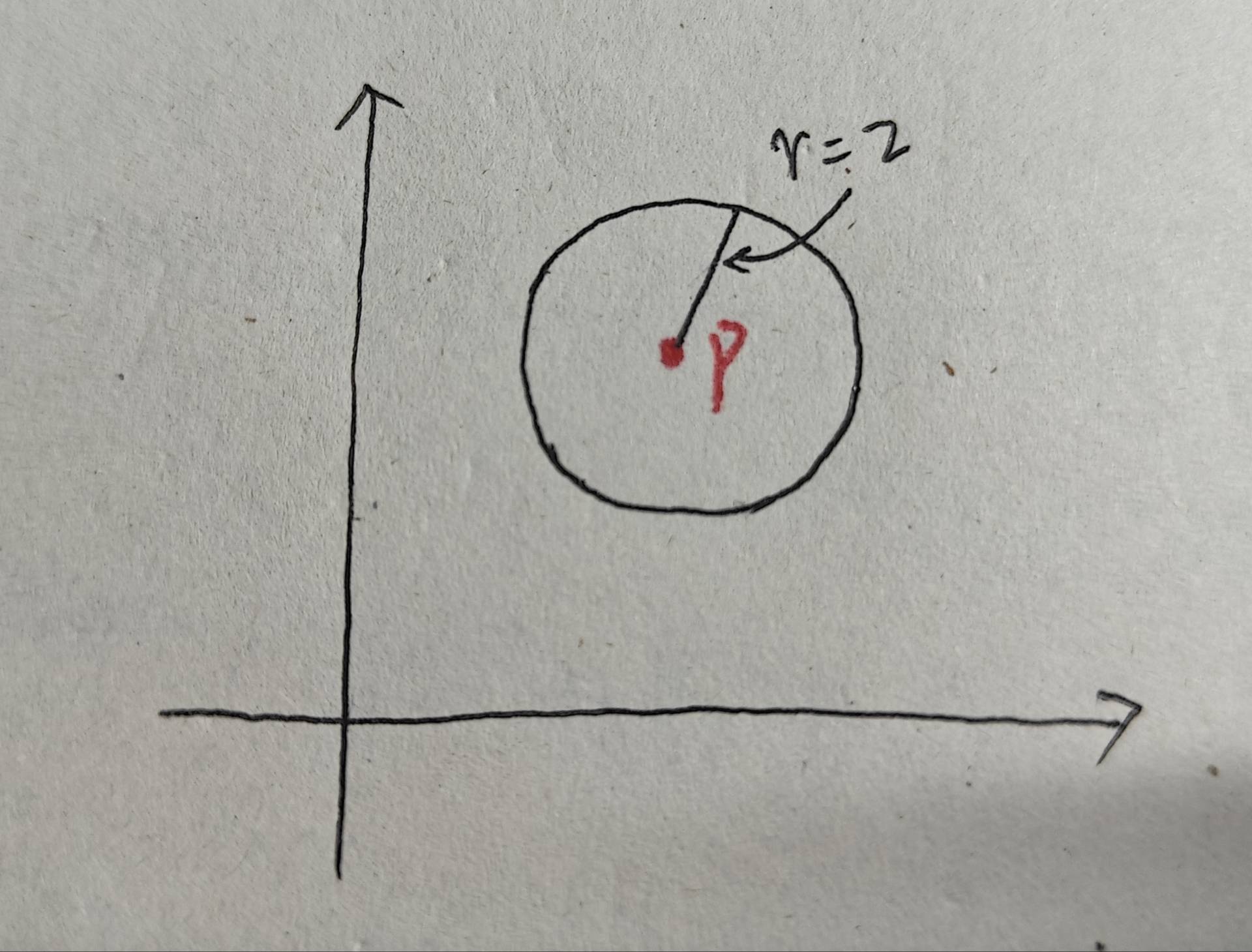
2、MinPts:核心点最小点数,由用户指定。
3、核心点:若点 p 的 ε 邻域内至少包含 MinPts 个点,则 p 是核心点。如下图所示:设MinPts为4,此时p点的ε 邻域内恰好有4个点(包含p本身),则p为核心点:
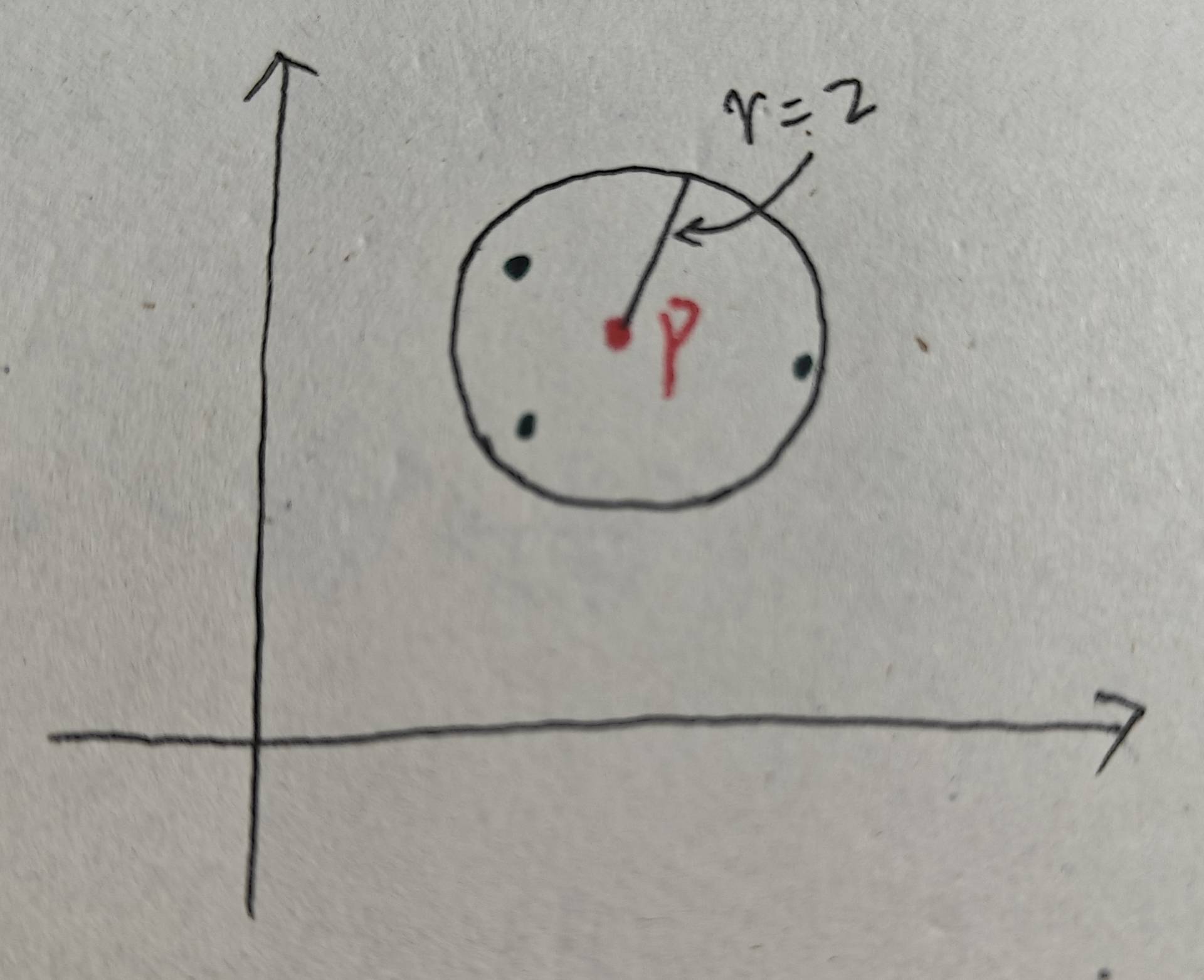
4、边界点:若点 p 的 ε 邻域内点的数量少于 MinPts,但它属于某个核心点的 ε 邻域,则 p 是边界点。如图,设Minpts = 4,已知核心点Q。如图,p点领域内只有两个点,因此p不是核心点,但是p在Q的ε 邻域内,因此p是边界点:
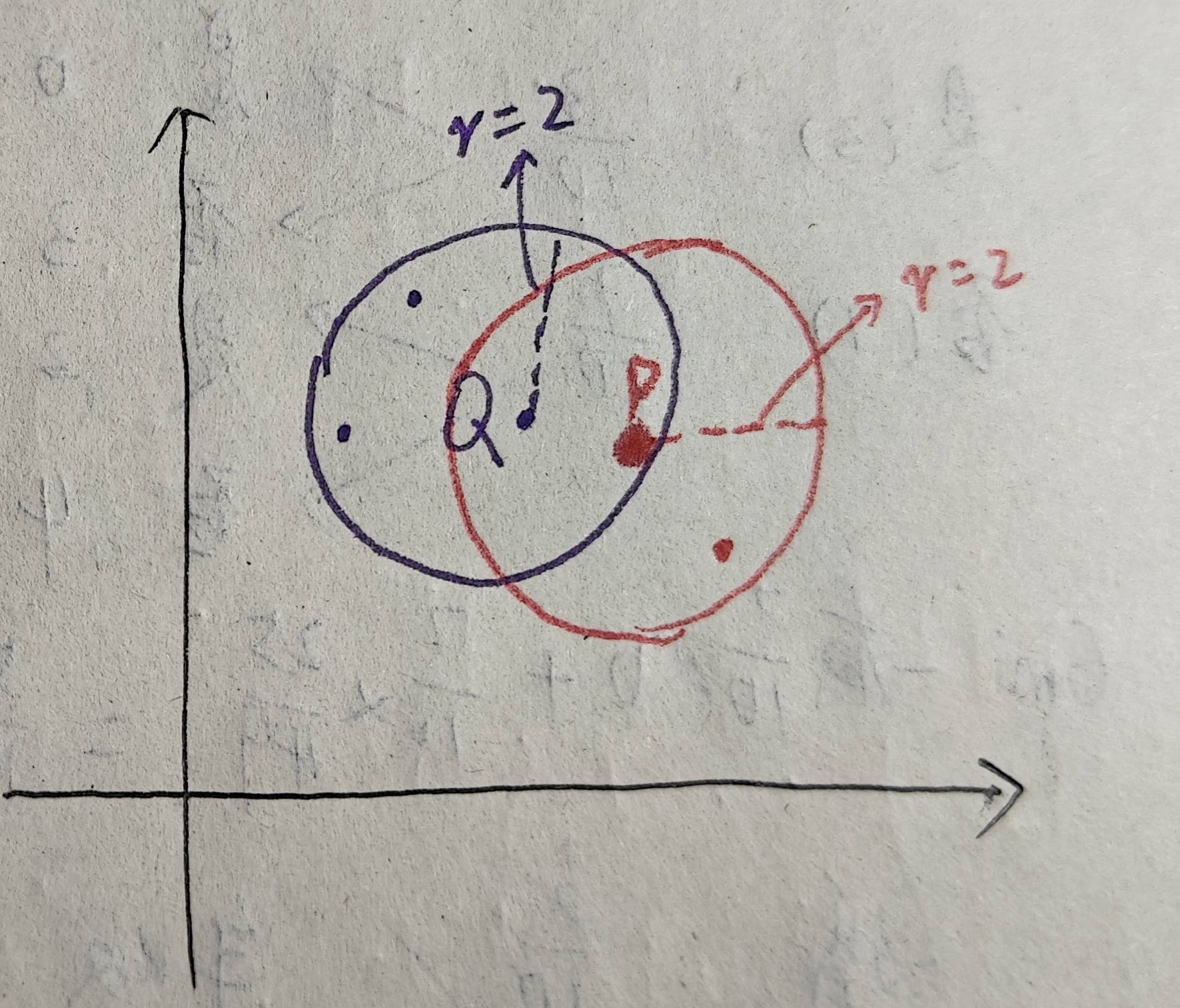
5、噪声点:既不是核心点也不是边界点的点。如下图所示,依然设MinPts = 4,p中只有两个点,小于MinPts,所以p不是核心点。又因为p也不属于其他核心点的ε 邻域领域,p也不是边界点。因此,p是噪声点:
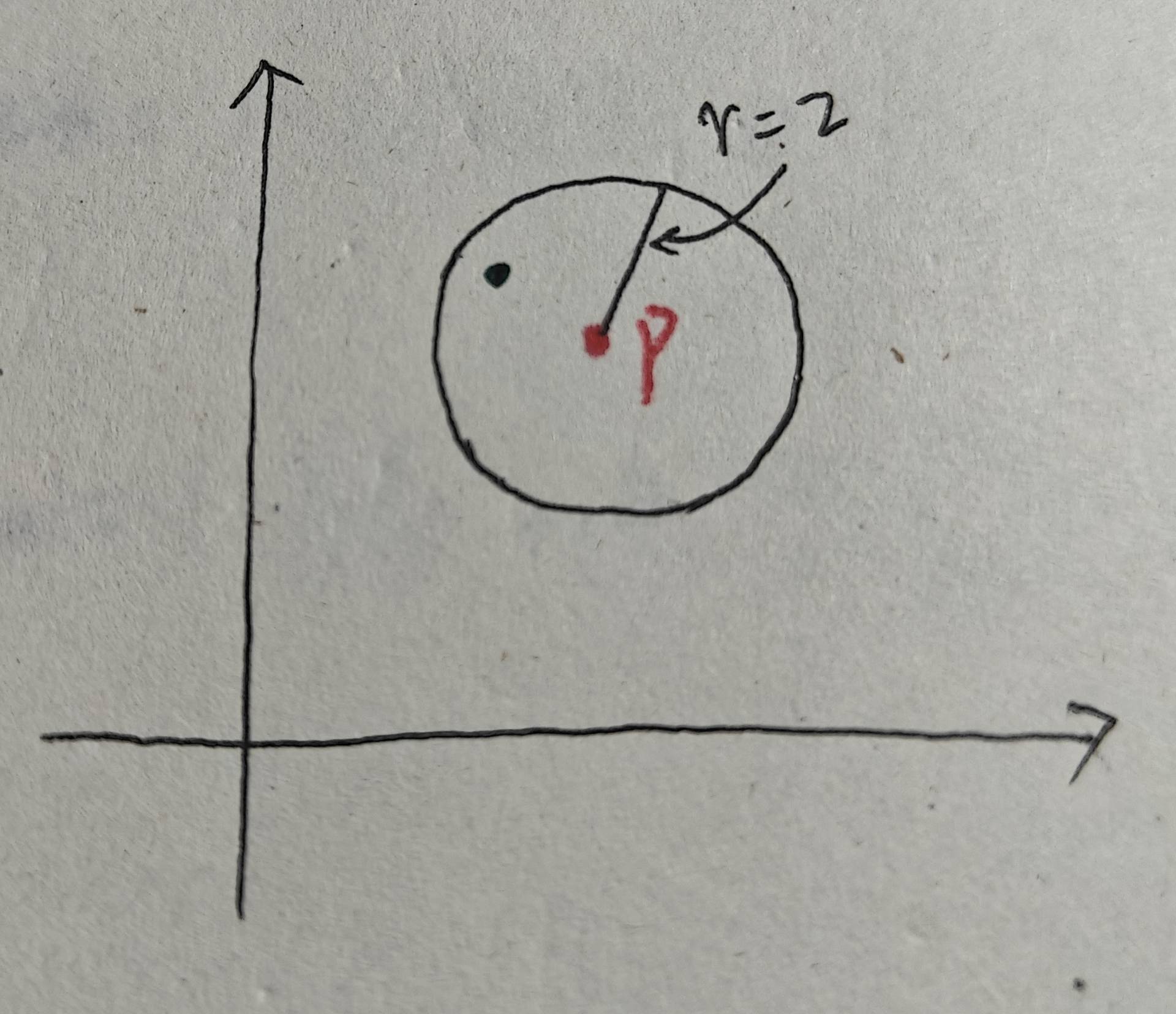
6、直接密度可达:若点 q 在核心点 p 的 ε 邻域内,则称 q 从 p 直接密度可达。
7、间接密度可达:若q1不在核心点p的ε 邻域内,q2在核心点p的ε 邻域内,且q1在q2的ε 邻域内,那么q1与p间接密度可达。
2、算法流程
1、参数设置:指定ε和 MinPts。
2、遍历所有的点:
若点 p 是核心点,创建一个新簇,并递归地将所有从 p 密度可达(直接+间接)的点加入该簇。
若点 p 是边界点或噪声点,暂时标记为未分类。
3、完成分类
3、算法示例
对以下数据点使用DBSCAN算法进行聚类。
这里指定ε = 2, MinPts = 3。
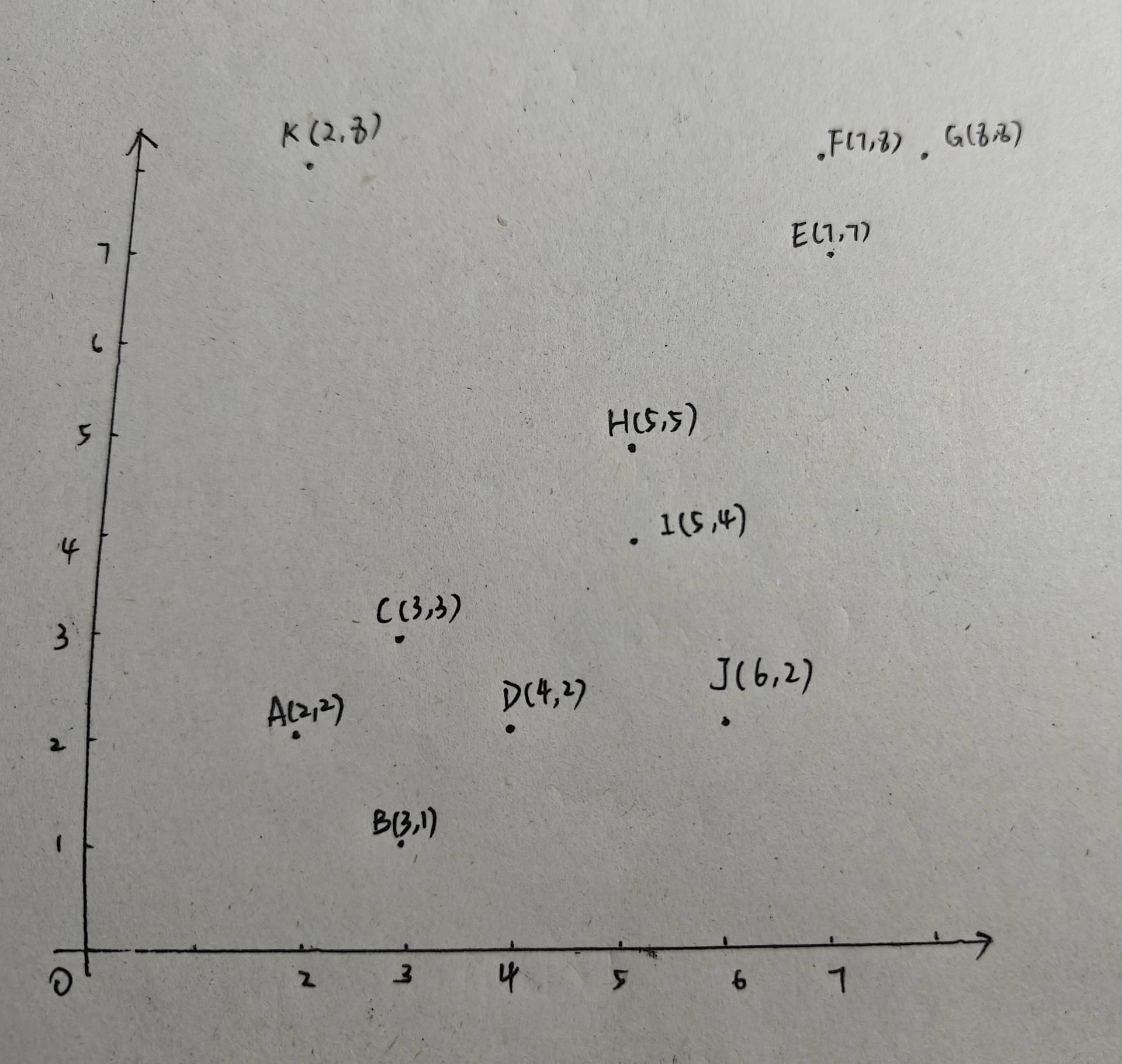
如图,对点A以2为半径画圆,可得A、B、C、D都在圆内,则A为核心点,可得第一个类:{A,B,C,D}。
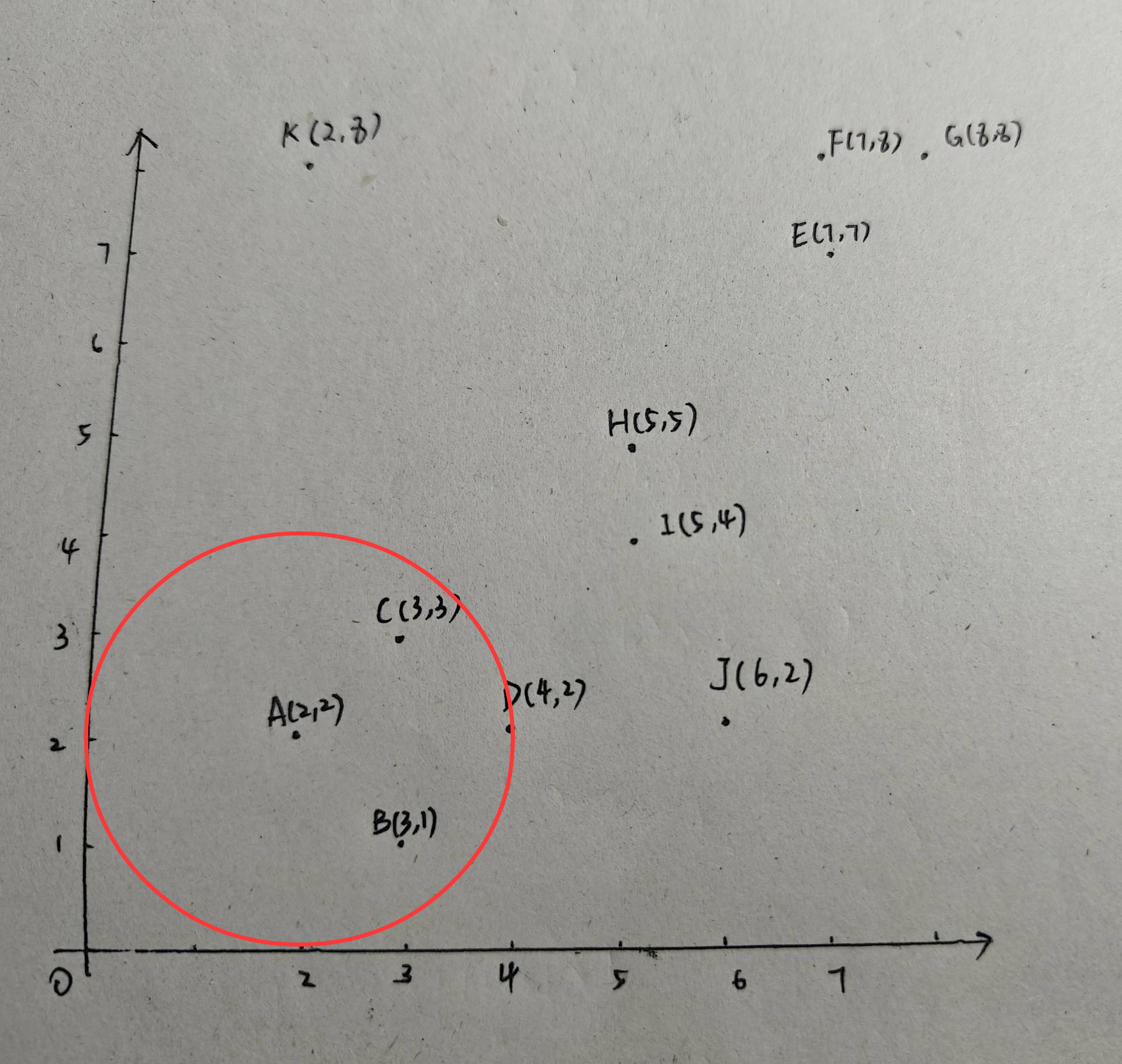
同理对B、C画圆,B、C都是核心点,由于B、C都在第一个类中了,因此没有新建类别,并且B、C的邻域中没有包含新的点,类别1仍为:{A,B,C,D}。接下来对D以2为半径画圆:
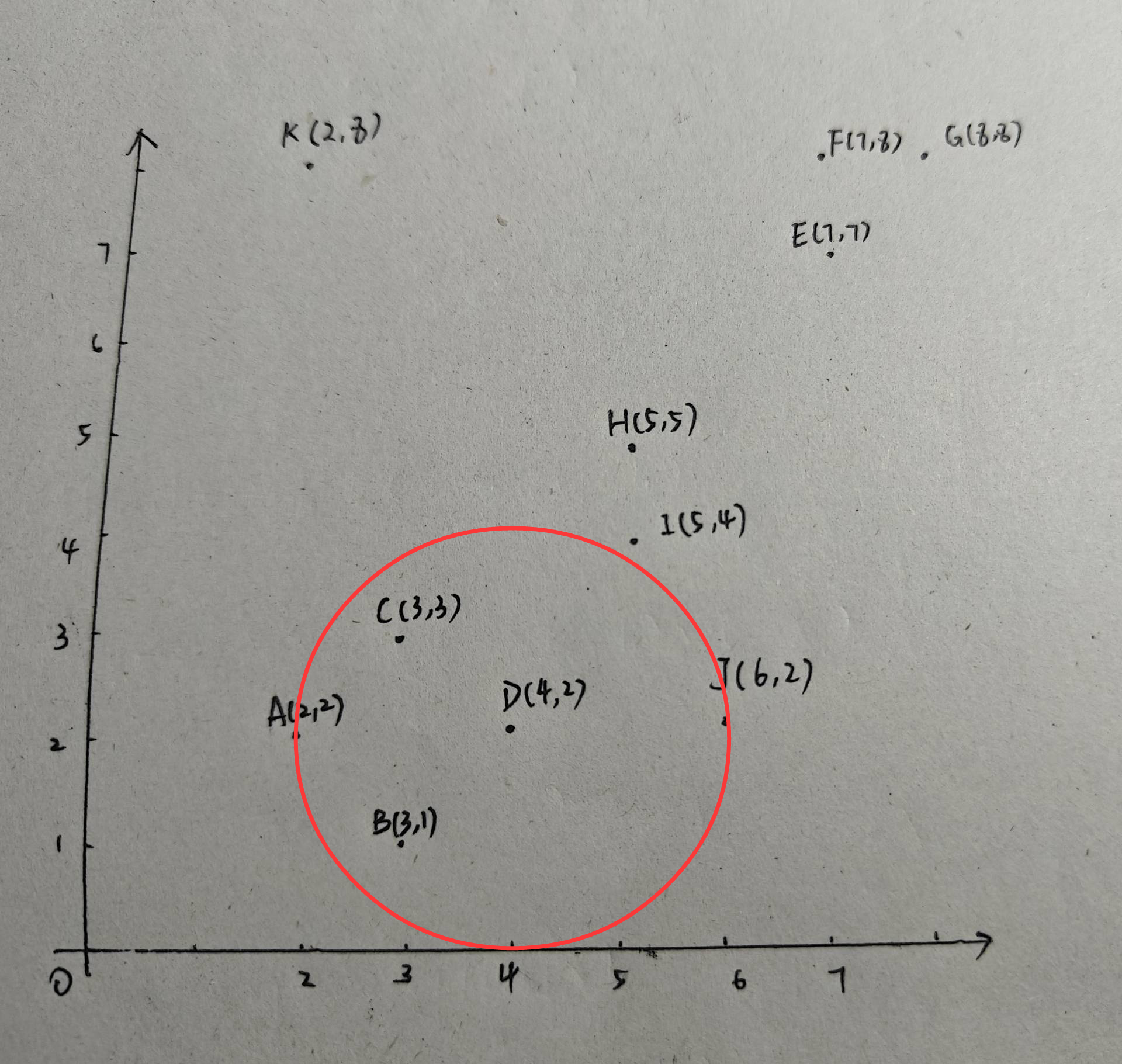
可见,D也是核心点,且D中包含了J,因此类别1进行更新:{A,B,C,D,J}。现在以E为圆心,2为半径画圆:
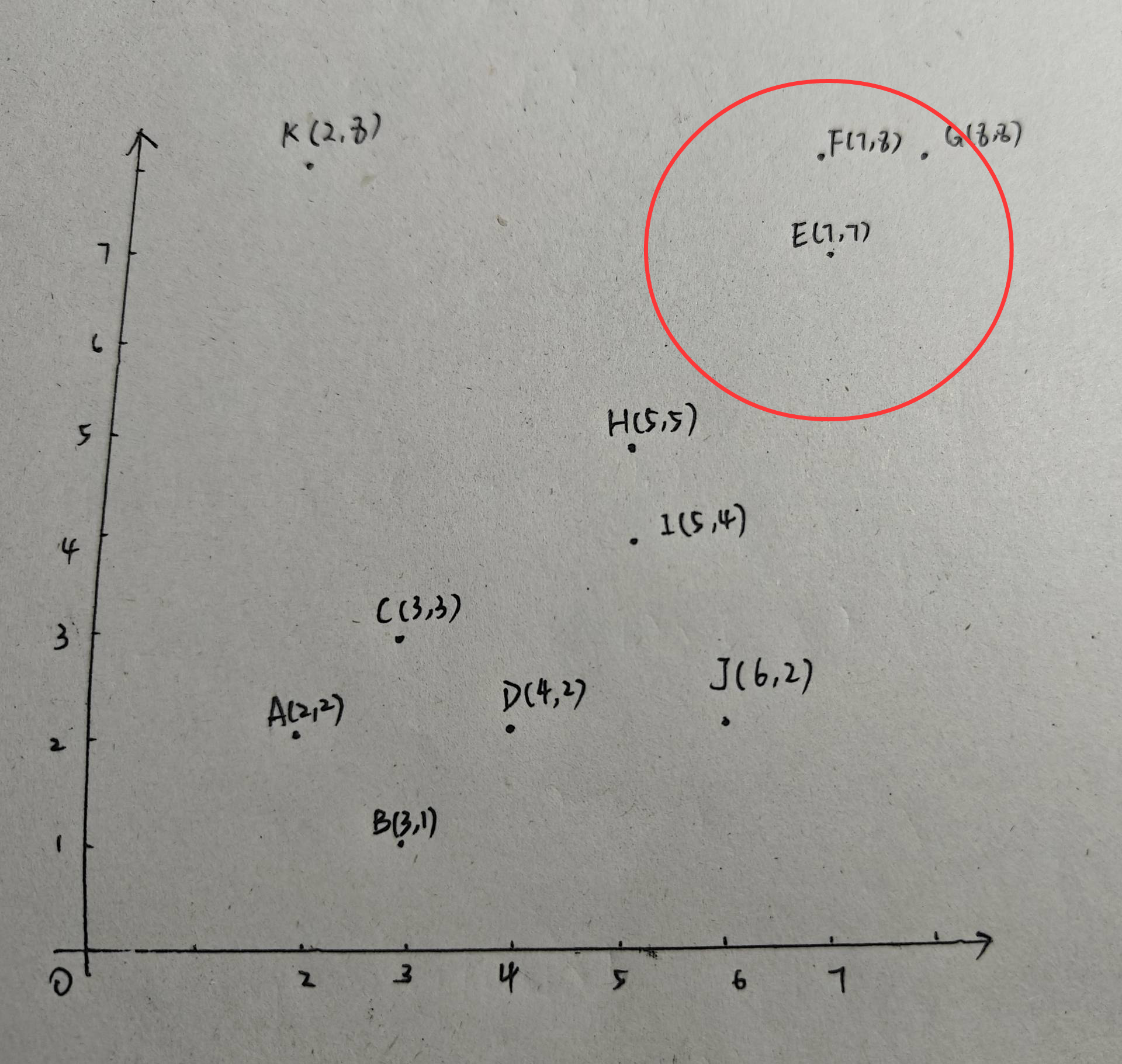
可以看出,E也是核心点,E、F、G都在圆内。由于此时并没有类别包含E,因此新建一个类2:{E、F、G}。至此,我们已经有两个类别:{A,B,C,D,J}、{E、F、G}。
同理,对F、G画圆,F、G都是核心点,由于F、G都在第二个类中了,因此没有新建类别,并且F、G的邻域中没有包含新的点,类别2仍为:E、F、G}。接下来,以点H为半径,2为圆心画圆:
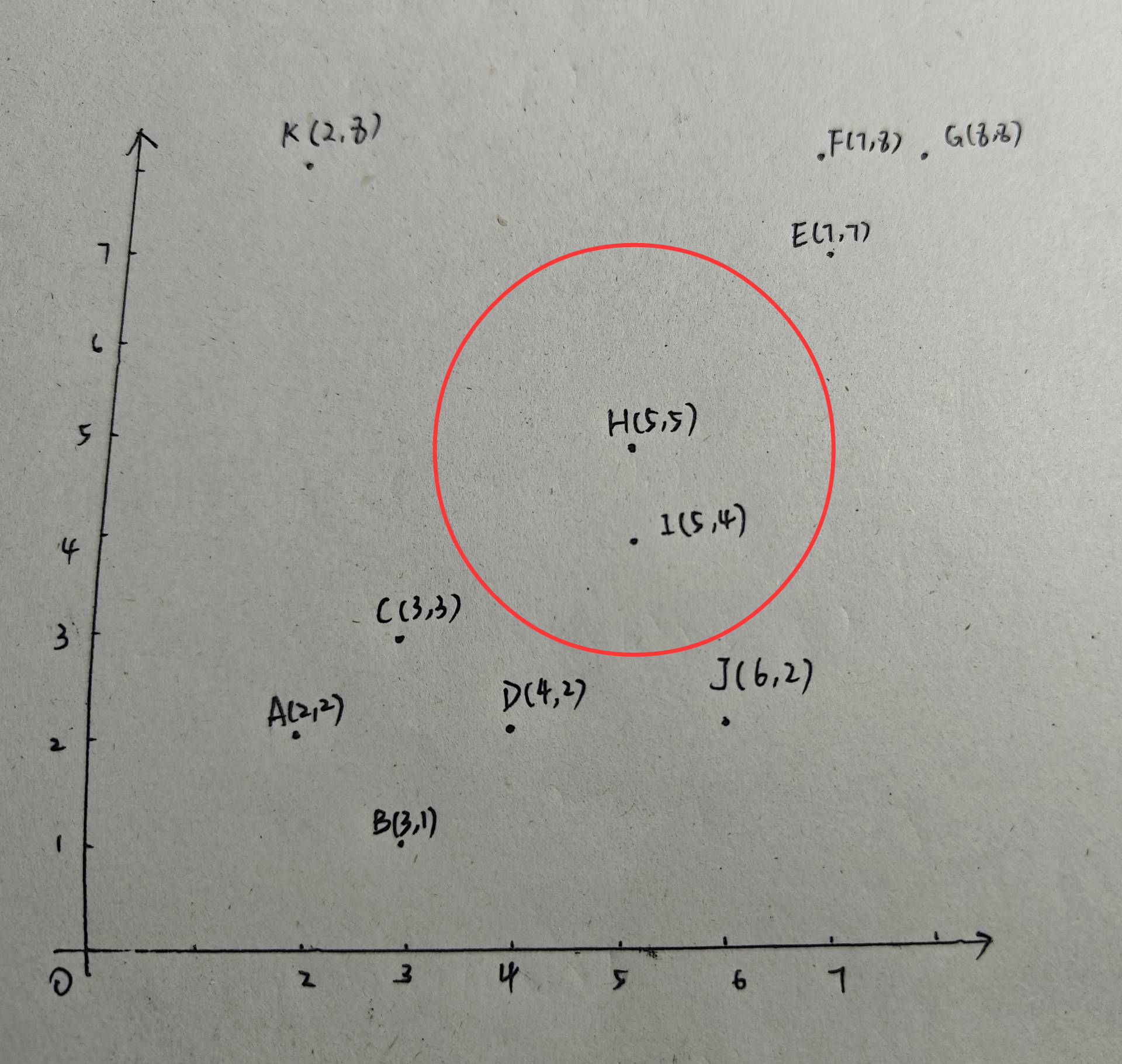
此时,H的邻域里只有两个点,H不是核心点,并且H此时也不能确定是不是边界点,因此暂时将H标记为噪声点。
接下来,以点I为半径,2为圆心画圆。I的邻域中有三个点:H、I、J。因此I是核心点。由于J已经属于类别1:{A,B,C,D,J},因此I、H均加入类别1,不新建类:{A,B,C,D,J,H,I}。可见,H由噪声点转变为了边界点。
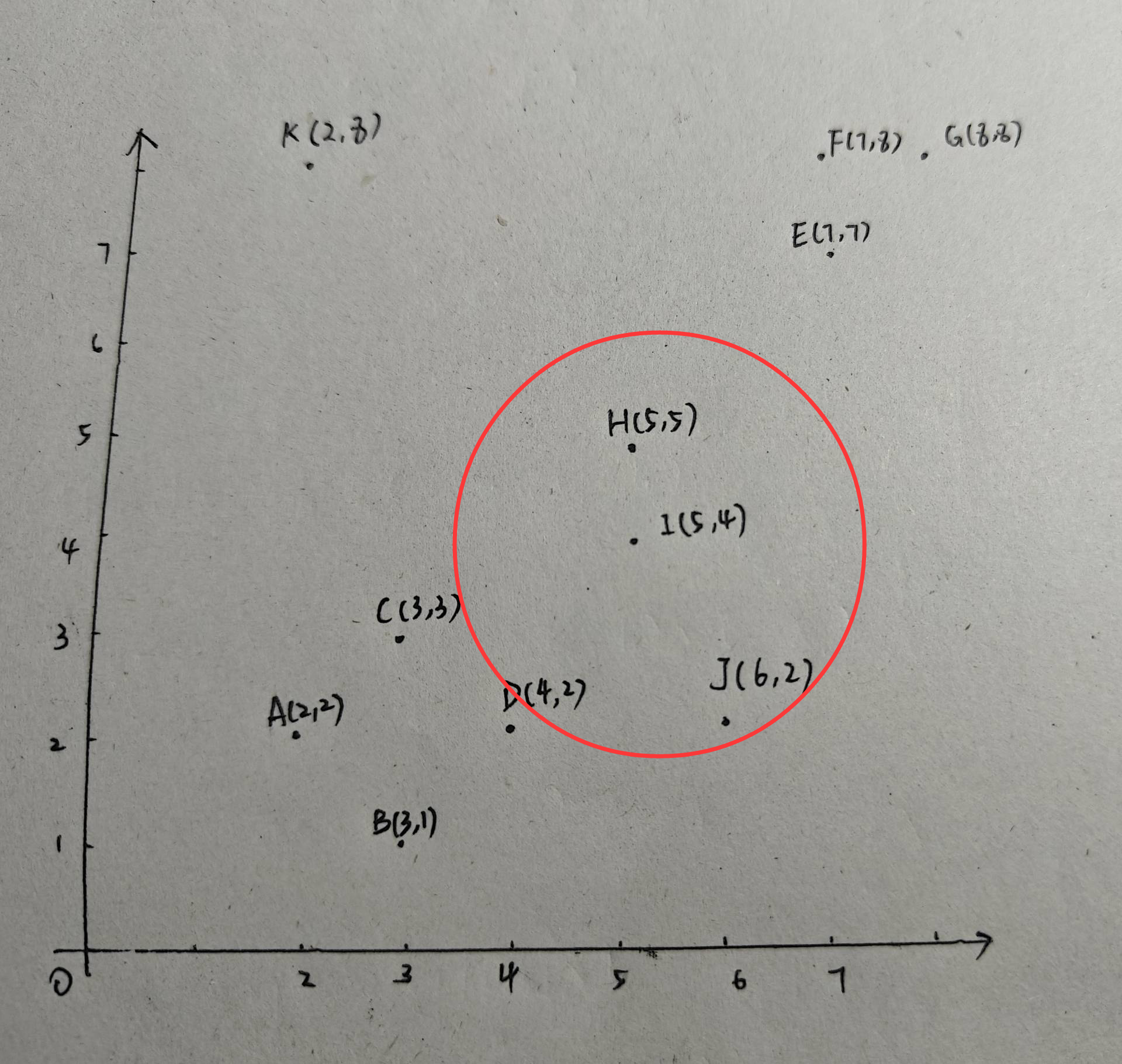
接下来,以J为圆心,2为半径画圆,J为核心点,但J已经在类别1中且没有引入新点,故类别1保持不变。最后以K为圆心,2为半径画圆,K不是核心点也不是边界点,因此K为噪声点。
最终结果为:类别1,{A,B,C,D,J,H,I};类别2,{E、F、G};噪声点:K
4、代码实现
import numpy as np
from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt# 示例数据
X = np.array([[1, 1], [2, 1], [1, 3], # 边界点和噪声点[8, 7], [8, 8], [9, 8], [10, 8], # 簇C1[5, 5] # 噪声点
])# 应用DBSCAN
dbscan = DBSCAN(eps=1.5, min_samples=2)
labels = dbscan.fit_predict(X)# 可视化
plt.figure(figsize=(8, 6))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=100)
plt.title('DBSCAN聚类结果 (ε=1.5, MinPts=2)')
plt.grid(True)
plt.show()print("聚类标签:", labels) # 输出: [ 0 0 -1 1 1 1 1 -1]
# -1表示噪声点,0和1表示两个不同的簇