机器学习 线性回归算法及案例实现
目录
一.核心思想
二.误差项
1.什么是误差(残差):
2.误差项特性:
3.误差项的分布规律
三.极大似然估计
四.线性回归API参数
五.线性回归模型的属性和方法
六.案例实现
1.一元线性回归
2.多元线性回归
3.糖尿病案例实现
一.核心思想
线性回归的核心是找到一条最优的直线(或超平面,针对多个自变量),使得该直线尽可能接近所有数据点,即让实际观测值与直线上的预测值之间的误差最小化。
-
对于单自变量(一元线性回归),模型可表示为:(y = wx + b\) 其中,y 是因变量(被预测的变量),x 是自变量(用于预测的变量),w 是斜率(表示自变量对因变量的影响程度),b 是截距(当自变量为 0 时因变量的取值)。
-
对于多自变量(多元线性回归),模型扩展为:y = w1x1 + w2x2 + ... + wnxn + b 其中x1, x2, ..., xn是多个自变量,w1, w2, ..., wn 是各自的系数,代表每个自变量对因变量的独立影响。
二.误差项
1.什么是误差(残差):
实际观测值 y 与模型预测值y^之间的差异,即 e = y - y^。线性回归的目标是使所有残差的平方和最小(最小二乘法)
2.误差项特性:
- 必然存在,自然界中产生的数据普遍存在波动和误差,因此误差项是不可避免的。
- 服从正态分布(大部分误差集中在零附近,极少数偏离较远)
3.误差项的分布规律
- 误差项服从正态分布(高斯分布),其概率密度函数表现为:
- 误差值为零时概率最大(因模型拟合时尽量使数据点靠近预测线)。
- 误差值远离零的概率逐渐减小(极端误差出现的概率极低)。
三.极大似然估计
极大似然估计可以作为线性回归模型中参数(如斜率、截距)的估计手段
极大似然估计的含义是指世界发生的事件都是最大概率出现的事件,由内部规律支撑其必然性。例如买彩票:单次购买不中是大概率事件,而多次购买中奖是必然结果。
真实发生的事件均为大概率事件,小概率事件仅针对个体(如张三出门被车撞),但需结合全局数据(如几千人出行仅一人出事)才能体现规律。
四.线性回归API参数
源码如下: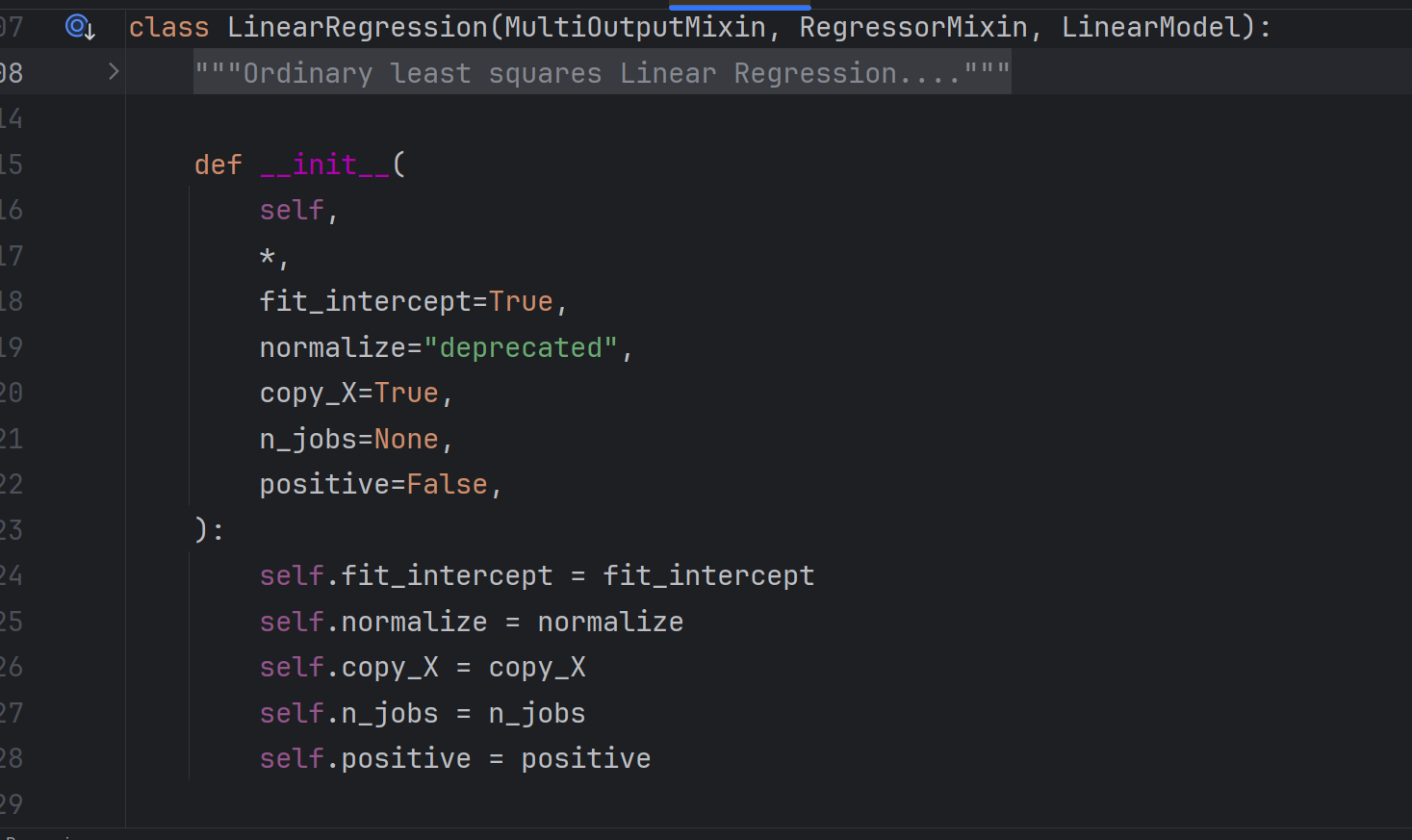
- fit_intercept:是否包含截距(β₀),默认
True(建议保留,避免强制过原点)。 - normalize:归一化,默认
False。 - copy_X:是否复制输入数据,默认
True(通常无需额外复制)。 - n_jobs:并行任务数,
-1表示使用所有 CPU 核心,大规模数据可加速计算;默认None(单进程)。
五.线性回归模型的属性和方法
- 属性:
coef_:特征系数(β₁, β₂, ...)。intercept_:截距值(β₀)。
- 方法:
fit():训练模型。predict():预测结果。score():模型评分。
六.案例实现
1.一元线性回归
使用广告投入(X)和销售额(Y)的模拟数据演示一元线性回归。
data.csv数据如下:
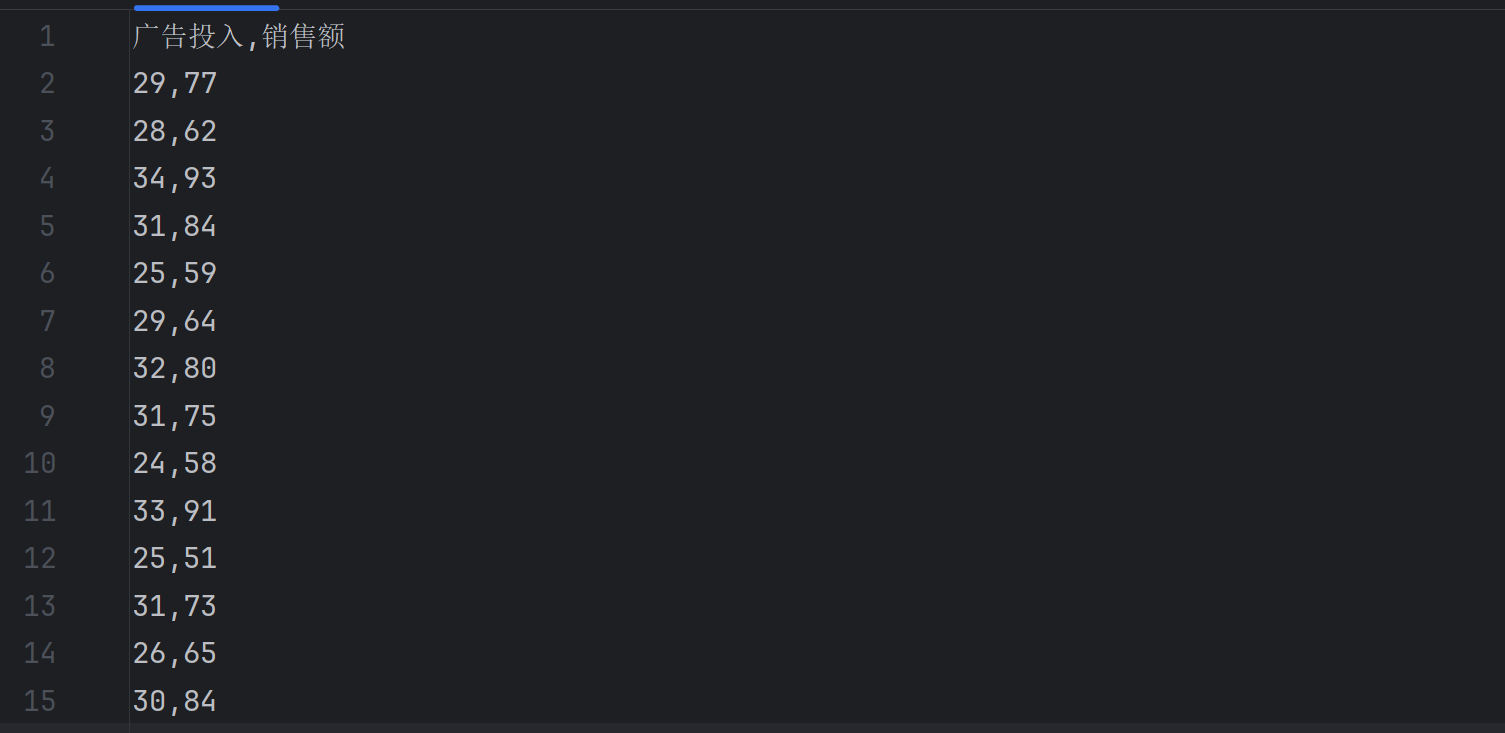
导入相关的库
import pandas as pd
from sklearn.linear_model import LinearRegression
数据含有列名我们用pandas库的read()方法读取数据
data = pd.read_csv('data.csv')计算算广告投入与销售额的相关系数(皮尔逊相关系数),结果为 0.9062,表明高度相关
corr=data[['广告投入','销售额']].corr()
print(corr)使用 LinearRegression 训练模型,并划分特征数据x与结果y
需要注意由于predict()方法中参数必须是二维的,fit()方法中的第一个参数必须是二维数组所以我们这里的x必须都是二维数据所以又加了一个中括号,y最好也写出二维数组
lr_model = LinearRegression()
x = data[['广告投入']]
y = data[['销售额']]调用fit()方法训练模型,并计算得分准确性
lr_model.fit(x,y)
score = lr_model.score(x,y)获取斜率和截距,建立回归方程
a=lr_model.coef_[0][0]
b=lr_model.intercept_[0]
print('y={}x+{}'.format(a,b))y=3.737885462555064x+-36.36123348017615预测数据
result1=lr_model.predict([[35]])
result2=lr_model.predict([[35],[45]])
print(result1,result2)[[94.46475771]] [[ 94.46475771][131.84361233]]完整代码
import pandas as pd
from sklearn.linear_model import LinearRegressiondata = pd.read_csv('data.csv')# 打印相关系数矩阵
corr=data[['广告投入','销售额']].corr()
print(corr)lr_model = LinearRegression()
x = data[['广告投入']]
y = data[['销售额']]lr_model.fit(x,y)
score = lr_model.score(x,y)a=lr_model.coef_[0][0]
b=lr_model.intercept_[0]
print('y={}x+{}'.format(a,b))result1=lr_model.predict([[35]])
result2=lr_model.predict([[35],[45]])
print(result1,result2)2.多元线性回归
以体重和年龄(X)预测血压收缩值(Y),数据包含多列特征。
数据内容如下:
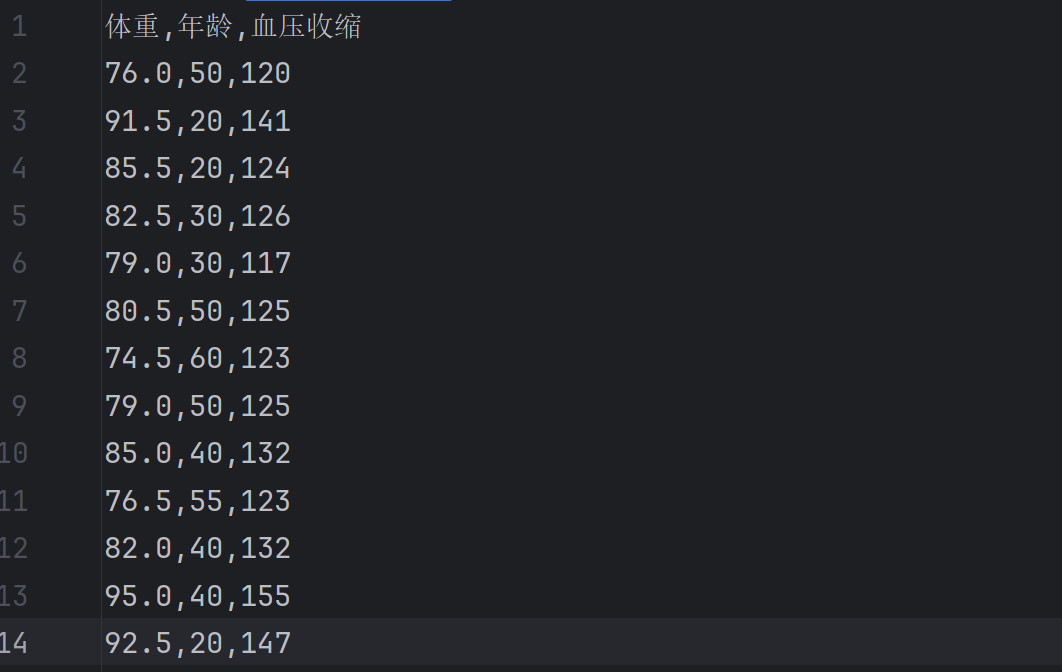
实现思路与一元线性回归大差不差,完整代码如下:
import pandas as pd
from sklearn.linear_model import LinearRegression
data = pd.read_csv('多元线性回归.csv',encoding='gbk')
corr = data[['体重','年龄','血压收缩']].corr()lr_model =LinearRegression()
x=data[['体重','年龄']]
y=data[['血压收缩']]
lr_model.fit(x,y)
score = lr_model.score(x,y)result1=lr_model.predict([[80,45]])
result2=lr_model.predict([[80,45],[95,25]])a1=lr_model.coef_[0][0]
a2=lr_model.coef_[0][1]
b=lr_model.intercept_[0]
print('y={}x1+{}x2+{}'.format(a1,a2,b))y=2.136558138364147x1+0.4002161546496849x2+-62.9633591124759563.糖尿病案例实现
提供 443 条糖尿病患者数据,目标变量(Y)为糖尿病指标值
分析特征X(如年龄、BMI、化验指标等)与目标变量的关系
糖尿病数据.csv数据如下:
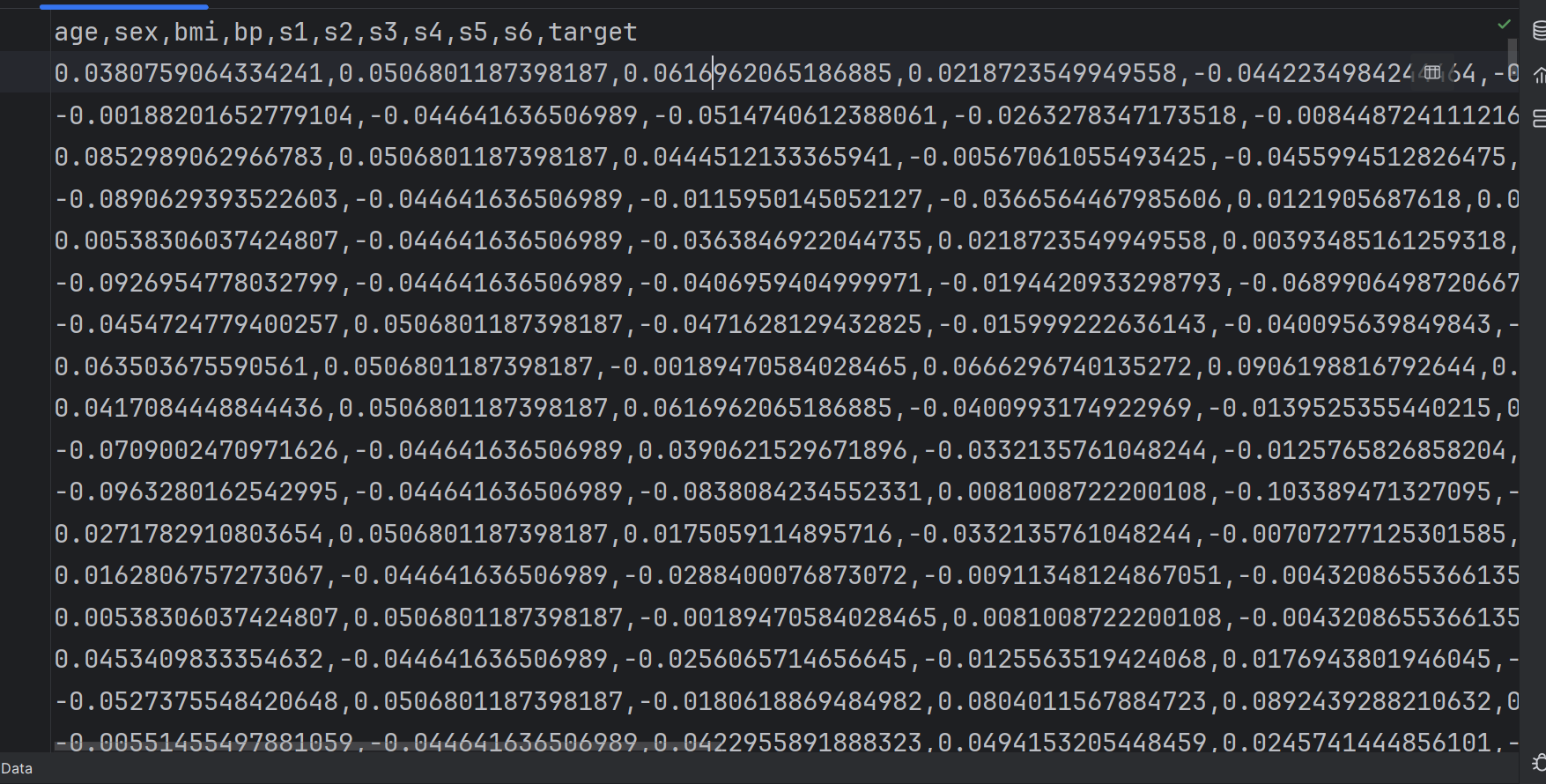
读取数据,并计算相关系数
import pandas as pd
from sklearn.linear_model import LinearRegression
data = pd.read_csv('糖尿病数据.csv')
corr=data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6','target']].corr()
利用pandas库的iloc方法划分数据集,我们将前220行作为训练集,其余作为测试集
train_data = data.iloc[:220,:]
test_data = data.iloc[220:,:]构建模型,并划分训练集的特征数据与预测结果,由数据内容可知最后一列为结果
lr_model = LinearRegression()
train_x=train_data.iloc[:,:-1]
train_y=train_data.iloc[:,-1]训练模型并计算得分
lr_model.fit(train_x,train_y)
score_train=lr_model.score(train_x,train_y)
print('score_train=',score_train)score_train= 0.4903256259671942划分训练集的特征数据与预测结果,然后将数据进行预测,计算得分
test_x=test_data.iloc[:,:-1]
test_y=test_data.iloc[:,-1]
lr_model.predict(test_x)
score_test=lr_model.score(test_x,test_y)
print('score_test=',score_test)score_test= 0.5253249763474657完整代码实现:
import pandas as pd
from sklearn.linear_model import LinearRegression
data = pd.read_csv('糖尿病数据.csv')
corr=data[['age','sex','bmi','bp','s1','s2','s3','s4','s5','s6','target']].corr()
print(corr)
train_data = data.iloc[:220,:]
test_data = data.iloc[220:,:]lr_model = LinearRegression()
train_x=train_data.iloc[:,:-1]
train_y=train_data[['target']]
lr_model.fit(train_x,train_y)
score_train=lr_model.score(train_x,train_y)
print('score_train=',score_train)test_x=test_data.iloc[:,:-1]
test_y=test_data[['target']]
lr_model.predict(test_x)
score_test=lr_model.score(test_x,test_y)
print('score_test=',score_test)
