当前位置：首页 > news >正文

深入理解图像插值：从原理到应用

news 2025/8/2 20:53:49

图像插值简介

图像插值（Image Interpolation）技术，是现代图像处理领域不可或缺的基础模块，无论是在缩放图像、图像旋转、医学图像配准、视频处理，还是在深度学习的超分辨率网络中，插值算法都扮演着“像素之间的桥梁”的角色。

在深入讲解图像插值理论之前，我们首先对图像插值的应用进行一个简单的介绍。图像插值在不同应用中都扮演着重要的基础支撑功能，因此我们有必要深入理解图像插值的所有细节内容。

图像缩放（Image Resizing）是图像处理中的基本操作之一。无论是缩小用于加快显示，还是放大以便细节观察或适配更高分辨率的设备屏幕，都不可避免地涉及插值算法的选择与实现。在缩放操作中，原始图像中的像素点数量必须被重新映射到目标图像的尺寸上。由于目标图像的像素位置通常不与原始像素精确对齐，这就需要对原图中临近像素进行“估计”以生成新像素值。
在图像几何变换（Geometric Transformations）中，图像插值是不可或缺的基础步骤之一。几何变换通常涉及坐标映射，比如平移、旋转、仿射变换、透视变换等。这些变换后的目标图像像素位置往往不再对应整数坐标，因此必须通过插值计算出这些位置上的像素值。
在超分辨率重建（Super-Resolution）中，我们期望将将低分辨率图像恢复为高分辨率图像。插值作为上采样的第一步（例如 bicubic 插值将图像从 100×100 放大到 200×200），提供初始估计值。结合神经网络（如SRCNN、ESPCN）时，插值可用作预处理，先扩大图像后输入网络。
在ISP(Image Signal Process)领域，数字彩色阵列（如 Bayer）只能记录单通道信息，需要插值得出完整的 RGB 图像。
在图像去模糊（Deblurring）的应用中，图像由于相机抖动、运动或镜头失焦而产生模糊。我们可将图像变换到频域中，然后再对频域进行插值以填补丢失频域信息，最终反变换回图像空间域期望获得更清晰的图像。
在多视图立体匹配（Multi-view Stereo）的应用中，我们使用多张图像重建三维模型，需要对多个图像中的像素进行对齐或匹配，插值可用于将图像中某一视角的像素“投影”到其他图像视角，从而实现一个统一坐标下的配准图像序列。
在视频处理应用领域，我们除了可以生成高分辨率的视频数据，也可以通过帧插值获得高帧率视频。如结合光流对齐视频帧，然后在对齐视频上进行帧插值则实现视频帧率提升。

多项式插值

基本定义

给定一组离散点 $(x_{1},y_{1}),(x_{2},y{{2}}),...,(x_{n},y_{n})$ ，我们期望获得在 $[x_{1},x_{n}]$ 区间上任意一点的 $y$ 值。也就是说需要找到一个多项式函数 $y=f(x)$ ，使其满足 $y_{1}=f(x_{1}),...,y_{n}=f(x_{n})$ 。

更直观得说，通过给定一系列点，我们希望获得经过给定点的唯一多项式函数。然后在代入任意坐标（ $[x_{1},x_{n}]$ 区间内），获得任意坐标下的估计值。

线性插值

如给定两个已知点 $(x_{1},y_{1}),(x_{2},y_{2})$ ，我们可以获得直线方程，如下：

假设直线上任意点坐标为 $(x,y)$ ，有方程 $\frac{y-y{1}}{x-x_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ ，

通过适当变换得： $(y-y_{1})(x_{2}-x_{1})=(x-x_{1})(y_{2}-y_{1})$ ，将任意点代入方程，可计算出对应得函数值。这就是最基本得插值方式：线性插值。后续通过适当变换与拓展就得到了图像中得双线性插值。

二次插值

有了线性插值，很自然得我们会考虑使用二次函数拟合离散点。二次函数得数学表达式如下：

$y=ax^{2}+bx+c$ ，该函数有参数 $(a,b,c)$ 唯一确定。因此，我们需要三个点以获得该区域上的二次曲线：已知三个离散点 $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ ，经过离散点可确定唯一的二次曲线：

代入离散点得： $\left\{\begin{matrix} y_{1}=ax_{1}^{2}+bx_{1}+c\\ y_{2}=ax_{2}^{2}+bx_{2}+c\\ y_{3}=ax_{3}^{2}+bx_{3}+c \end{matrix}\right.$ ，这里的 $x_{i},x_{i}^{2},y_{i}$ 均为已知量， $(a,b,c)$ 作为方程组的位置量，因此我们可以求解线性方程组获得 $(a,b,c)$ 的值。

矩阵表达为： $\begin{bmatrix} x_{1}^{2} & x_{1} & 1\\ x_{2}^{2}& x_{2}& 1\\ x_{3}^{2}& x_{3} & 1 \end{bmatrix}\begin{bmatrix} a\\ b \\ c \end{bmatrix}=\begin{bmatrix} y_{1}\\ y_{2} \\ y_{3} \end{bmatrix}$ ，如果 $\begin{bmatrix} x_{1}^{2} & x_{1} & 1\\ x_{2}^{2} & x_{2}&1 \\ x_{3}^{2} & x_{3} & 1 \end{bmatrix}$ 可逆，则可确定唯一的 $\begin{bmatrix} a\\ b \\ c \end{bmatrix}$ 。这里选择三个不共线的点是矩阵可逆的充分必要条件。如果三个点共线，则退化成一条直线。

三次插值

使用二次插值同样的思路，我们可以构造三次曲线。已知四个点 $(x_{1},y_{1}),...,(x_{4},y_{4})$ ，可确定三次函数 $y=ax^{3}+bx^{2}+cx +d$ 的所有系数 $(a,b,c,d)$ 。我们可以使用与二次插值中所介绍的方法进行求解，只需要拓展线性方程组的维度即可。

拉格朗日(Lagrange)插值拟合任意多项式

一般的多项式插值为线性插值，二次插值与三次插值。使用拉格朗日(Lagrange)插值，我们可以统一任意阶的多项式插值。同时，由于拉格朗日插值不需要显示计算出多项式的系数，在计算效率上会更加有优势。结合Newton均差，我们可以采用渐进的方式计算相邻区域的插值，这会进一步提升计算效率。这里，我们仅介绍拉格朗日插值，Newton均差仅在数值计算上对拉格朗日插值进行了一个改造，其目的就是为了实现邻域上的迭代计算。

给 $n$ 个定点对 $(x_{1},y_{1}),...,(x_{n},y_{n})$ ，我们可以写出一个 $n-1$ 阶的多项式，使得所有点都满足该方程。此时，在区间 $[x_{1},x_{n}]$ 内任意点 $x$ 所对应的 $y$ 值可直接表示为：

$y(x)=y_{1}\frac{(x-x_{2})(x-x_{3})...(x-x_{n})}{(x1-x_{2})(x1-x_{3})...(x1-x_{n})}+y_{2}\frac{(x-x_{1})(x-x_{3})...(x-x_{n})}{(x2-x_{1})(x2-x_{3})...(x2-x_{n})}+...$ ，

对于该公式，我们这里作一些简单说明：

当 $x=x_{n}$ 时， $y(x)=y(x_{n})=y_{n}$ ;
当 $x\neq x_{n}$ 时， $y(x)$ 为 $y_{1},...,y_{n}$ 的线性组合；
已知 $n$ 个点对，可以唯一确定一个 $n-1$ 阶的多项式，使得所有 $n$ 个点均满足该多项式；
拉格朗日(Lagrange)插值获得的多项式曲线，与之前使用线性代方程组显示求解的多项式曲线是一致的；
通过引入拉格朗日(Lagrange)插值，我们统一了所有的多项式插值算法；

接下来给出一些具体案例：

给定两个点对，拉格朗日插值可表示为： $y(x)=y_{1}\frac{x-x_{2}}{x_{1}-x_{2}}+y_{2}\frac{x-x_{1}}{x_{2}-x_{1}}$ ，这就是我们在实际应用中所使用的线性插值（这里特别要注意表达式中分母的符号）。

类似得，给定四个点对得到三次方程，这与显示求解的三次方程是一致的。表达如下： $y(x)=y_{1}\frac{(x-x_{2})(x-x_{3})(x-x_{4})}{(x_{1}-x_{2})(x_{1}-x_{3})(x_{1}-x_{4})}+y_{2}\frac{(x-x_{1})(x-x_{3})(x-x_{4})}{(x_{2}-x_{1})(x_{2}-x_{3})(x_{2}-x_{4})}+y_{3}\frac{(x-x_{1})(x-x_{2})(x-x_{4})}{(x_{3}-x_{1})(x_{3}-x_{2})(x_{3}-x_{4})}+y_{4}\frac{(x-x_{1})(x-x_{2})(x-x_{3})}{(x_{4}-x_{1})(x_{4}-x_{2})(x_{4}-x_{3})}$ ，要想求得拟合区间内任意 $x$ 所对应的 $y$ 值，将 $x$ 赋值代入公式即可。

图像插值

在"多项式插值"部分，我们从数学角度理解了插值的基本原理。图像的插值技术遵循多项式插值的基本思想，但也根据图像的基本特点进行了一些改进。OpenCV提供的函数cv::resize实现了多种插值方式，下面我们结合该函数的插值参数对图像插值进行详细讨论。

最邻近插值(cv::INTER_LINEAR)

这是最简单也最高效的插值方式，同时也是插值后视觉效果（图像连续性）最差的插值方式。在某些效率优先图像应用中，我们可以选择这种插值方式。

最邻近插值的基本思想是：遍历目标图像上的所有点 $(x_{dst},y_{dst})$ 。首先计算出该点在原图像上的坐标 $(x_{src}, y_{src})$ 。一般情况下， $(x_{src}, y_{src})$ 都是非整数坐标。直接使用距离 $(x_{src}, y_{src})$ 最近的整数坐标 $(x_{src}^{int},y_{src}^{int})$ 上的像素值作为目标位置 $(x_{dst},y_{dst})$ 的像素值，这样就实现了最邻近插值。

这里我们强调一下图像插值的正确操作顺序：遍历目标图像上的所有点，然后计算每个目标图像点所对应的原图像坐标点(后续的所有插值都遵循这个规则)！这个操作变换顺序看起来有些怪异，我们可能更加容易接受的是遍历原图像上的所有点，然后再映射到目标图像上。如此逆向操作主要原因如下：

我们的目的是生成一个插值变换后的图像，如果遍历原图像所有像素点再进行映射，则可能在目标图像上有很多点并无对应。典型情况如将100*100的图像放大到1000*1000；
插值计算需要完整的邻域信息，遍历原图再映射使得插值需要在目标图像上进行，而此时的目标图像上并没有完整的有效数据，从而使得构造插值算法比较复杂；

双线性插值(cv::INTER_LINEAR)

双线性插值是图像处理中比较常用的插值方式，也是OpenCV很多函数默认的插值方式。双线性插值兼顾了插值效果与运行效率，所以会在多数情况下使用。

双线性插值就是线性插值，"双"表示两个方向上进行线性插值，这是由于图像为二维数据，而线性插值讨论的是一维数据。

如 $\begin{bmatrix} 10 &15 \\ 7 & 9 \end{bmatrix}$ 表示 $P_{0,0}=10,P_{0,1}=15,P_{1,0}=7,P_{1,1}=9$ ，则我们可以使用双线性插值计算出 $P_{0.4,0.8}$ 上的值，具体如下：

在 $x$ 方向上应用两次线性插值： $\left\{\begin{matrix} y_{0}=10*(1-0.4)+15 * 0.4=12\\ y_{1}=7*(1-0.4)+9*0.4=7.8 \end{matrix}\right.$ ，

在 $y$ 方向上应用一次线性插值： $P_{0.4,0.8}=y_{0}*(1-0.8)+y_{1}*0.8=8.64$ ，

至此，我们完成了双线性插值的计算。

双三次插值(cv::INTER_CUBIC)

为什么没有讨论双二次插值？其实，双二次插值可以直接基于二次插值拓展，但多数图像处理系统并没由构造该插值方式。主要原因是：二次插值的效果比三次插值效果差，但运行效率基本相当，所以我们在运行效率基本一致情况下选择了插值效果更好的三次插值。

类比双线性插值，双三次插值也表示在图像的两个维度上进行插值。那么，我们是否可以直接应用拉格朗日插值构造双三次插值呢？不能！因为三次插值存在震荡，不具备良好的局部可控性，因此不适应图像插值。

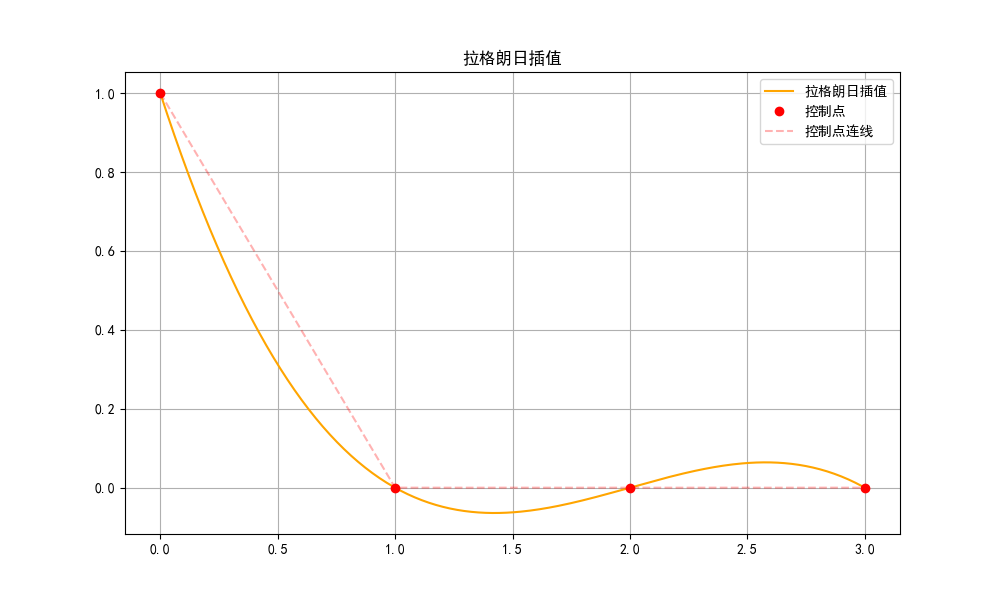
上图使用拉格朗日插值法对4个控制点构造的3次多项式，在区间 $[0,3]$ 上各个离散点取值为 $[1,0,0,0]$ ，很显然在区间 $[1,3]$ 上图像插值应该都为0，而此处出现了震荡！因此，我们需要寻找一个局部可控的三次插值方案！

Catmull-Rom 插值替代Lagrange插值

我们在构造三次插值过程中，真正关心的是在某个局部区间是否局部良好的平滑性，如在步长为1的区间 $[x,x+1]$ 上，我们需要构造一个平滑的三次曲线，使得该区间上没有震荡性。

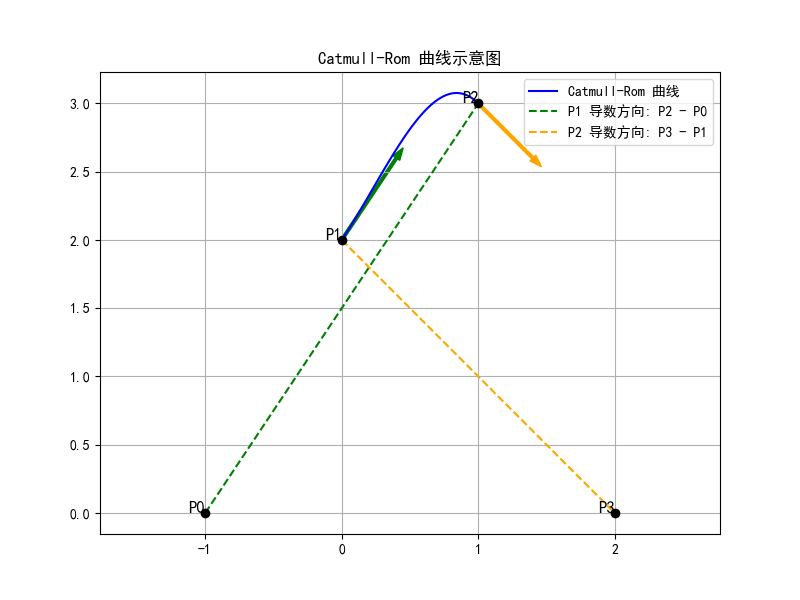
如上图所示，我们需要关注 $[P1,P2]$ 区间上的插值。给出4个控制点 $P0,P1,P2,P3$ ，使得区间 $[P1,P2]$ 上的拟合曲线为三次曲线，同时满足：

$P1$ 处的曲线斜率等于 $P0P2$ 连线方向
$P2$ 处的曲线斜率等于 $P1P3$ 连线方向

通过以上关系，我们开始构造满足条件的三次函数 $y=c_{0}+c_{1}x+c_{2}x^{2}+c_{3}x^{3}$ 。在上图中，有效区间 $[0,1]$ 在其端点上的值可表示为 $P1,P2$ （这里使用符号以推导处通用的计算公式）。以上条件可表示为：

$y(0)=P1$
$y(1)=P2$
$y^{'}(0)=\frac{P2-P0}{1-(-1)}$
$y^{'}(1)=\frac{P3-P1}{2-0}$

代入到三次函数中有：

$c_{0}=P1$
$c_{0}+c_{1}+c_{2}+c_{3}=P2$
$c_{1}=\frac{P2-P0}{2}$
$c_{1}+2c_{2}+3c_{3}=\frac{P3-P1}{2}$

根据以上关系，我们可以求解出 $c_{0},c_{1},c_{2},c_{3}$ ，从而实现了Catmull-Rom曲线的拟合。该曲线位过 $P1,P2$ 点三次函数拟合，由于受到 $P0,P3$ 的约束，在 $P1,P2$ 区间具备良好的局部性（不震荡），该特性使得图像插值具备良好的视觉效果。

需要说明的是：使用Catmull-Rom拟合的曲线一般不过 $P0,P3$ 点，所以我们只能对 $P1,P2$ 区间进行插值。同时，我们可以通过控制 $P1,P2$ 端点斜率与对应控制点连线直接的关系改变拟合斜率，达到个性化拟合效果。

以上就是Catmull-Rom插值的基本原理，在图像插值应用中，我们一般使用Catmull-Rom插值拟合步长为1的区间上的三次函数，从而实现良好的插值效果。

Lanczos插值(cv::INTER_LANCZOS4)

为了得到更好的插值效果，我们可以使用Lanczos插值方式，但该算法的运行效率偏低。这是一个基于频域的插值方式，基本思想是将离散图像数据变换到频域，然后对频域进行插值得到连续的频域数据，最后再变换到空间与从而获得连续的图像。

该算法在实际实现中并没有进行频域转换，而是提前将低通滤波器变换到空间域(sinc函数)，再利用空间域的卷积实现连续函数的估计（即插值）。我们会在后期专门开辟一个图像复原相关的主题详细讲解频域插值的方案。这里我们可以将Lanczos插值看作一个比双三次插值效果更好，但计算复杂度更高的插值方案。

基于像素区域重采样(cv::INTER_AREA)

这不是一个新的插值算法，而是在应对大图像缩小小图像时的一种策略。如对4000*4000的图像缩小到100*100，采用常规插值方法可能产生振铃现象或者一些亮度突变问题。如果在缩小图像前将多个原像素合并为一个目标像素，则可避免振铃或亮度突变问题。

正如前面所诉，插值过程是遍历目标图像上所有像素，然后计算其对应原图像上的点，最后在原图像上一个小的邻域（如4*4）上进行插值拟合。如果原图像远大于目标图像(图像缩小情形)，则有很多点不会参与计算，这是导致振铃与亮度突变的根本原因。通过对原图像合并像素使得原图像上所有点都参与插值运算，从而解决振铃与亮度突变问题。

另外，如果我们在插值前对原图像进行适当的平滑处理，也同样达到像素合并的效果，从而也可以避免缩小后图像的振铃与亮度突变问题。

插值效果

图像放大插值

上图从上到下分别为：最邻近插值，双线性插值，双三次插值，Lanczos插值的效果。原始图像约为80*80，插值后图像为400*400。可以看出双三次与Lanczos插值效果都非常不错，最邻近插值效果最差，这与我们之前的理论分析非常吻合。

图像缩小插值

上图从上到下分别为：双三次插值与基于像素区域重采样。原始图像分辨率为3000*3000，缩小后图像分辨率为300*300。在图像缩小的插值中，双三次插值产生了亮度突变，而基于像素区域重采样插值得到了很好的效果。这里需要说明的是：OpenCV基于像素区域重采样使用的插值算法一般是双三次插值，只是在插值前合并了像素是使所有像素均参与插值运算，从而避免振铃或者亮度突变问题。

Windows GDI显示上的应用

在Windows的GDI显示系统上，通过函数SetStretchBltMode可设备不同策略的插值模式。插值模式会影响StretchBlt，GdiAlphaBlend等函数，使他们选择不同的插值方式进行绘制。插值模式主要包括：COLORONCOLOR和HALFTONE，其中COLORONCOLOR类似最邻近插值，HALFTONE类似双线性插值。

在Windows系统上对图像进行放大显示时，我们需要使用HALFTONE以获得比较平滑的显示效果。在对图像进行缩小显示时，GDI并没有提供类似区域重采样的策略，我们可以首先对原图进行平滑处理，然后再缩小显示，这样也能达到像素区域重采样的目的。

总结

本文首先讲解了多项式插值（线性、二次、三次）和拉格朗日插值的基本原理，然后分析了图像处理中的五种插值算法：最邻近插值（简单但效果差）、双线性插值（效率与效果平衡）、双三次插值（基于Catmull-Rom改进）、Lanczos插值（效果最好但复杂）和区域重采样（适合缩小图像），最后通过实例对比展示不同插值方法在图像放大和缩小时的效果差异。同时，我们也同步说明了Windows GDI系统中的插值应用，这对于基于C++的桌面开发有一定帮助。在文章开头，我们罗列了很多关于插值算法的应用，在后续章节我们会根据情况单独形成博文，以供大家参考。

查看全文

http://www.dtcms.com/a/304349.html