【初识数据结构】CS61B中的基数排序
本教程介绍 CS61B 中的基数排序,这是一种可以在某些情况下甚至超越归并排序、快速排序的特殊的排序方法,但是牺牲了内存空间
计数排序
连续编号情形
我们需要对一个编号从 0 到 11 的表进行排序
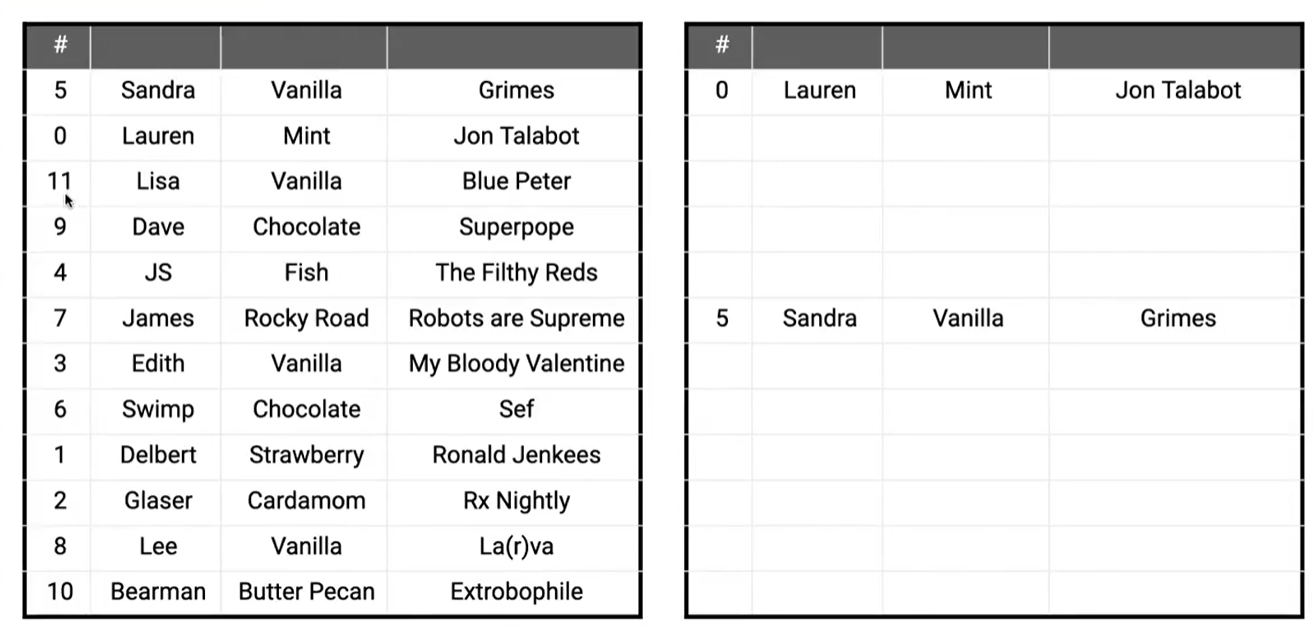
实际上我们可以拿出另一张同样大小的空白表,在遍历左边表时,我们不需要进行比较,就可以直接将元素填到正确的位置上!
这样我们的时间复杂度来到了 θ(N)\theta(N)θ(N),避免了之前我们提到的 NlogNNlogNNlogN 界限
但这种情况你必须保证编号是连续的
花色分类情形

我们要考虑的问题是,我怎么知道第一个红桃应该放在哪里呢?
我们要做的是,扫描两次,第一次扫描来计数每个相同的元素有多少个(同时根据优先级,我们可以知道每个元素的索引是多少),第二次扫描根据第一次扫描的结果来进行放置。
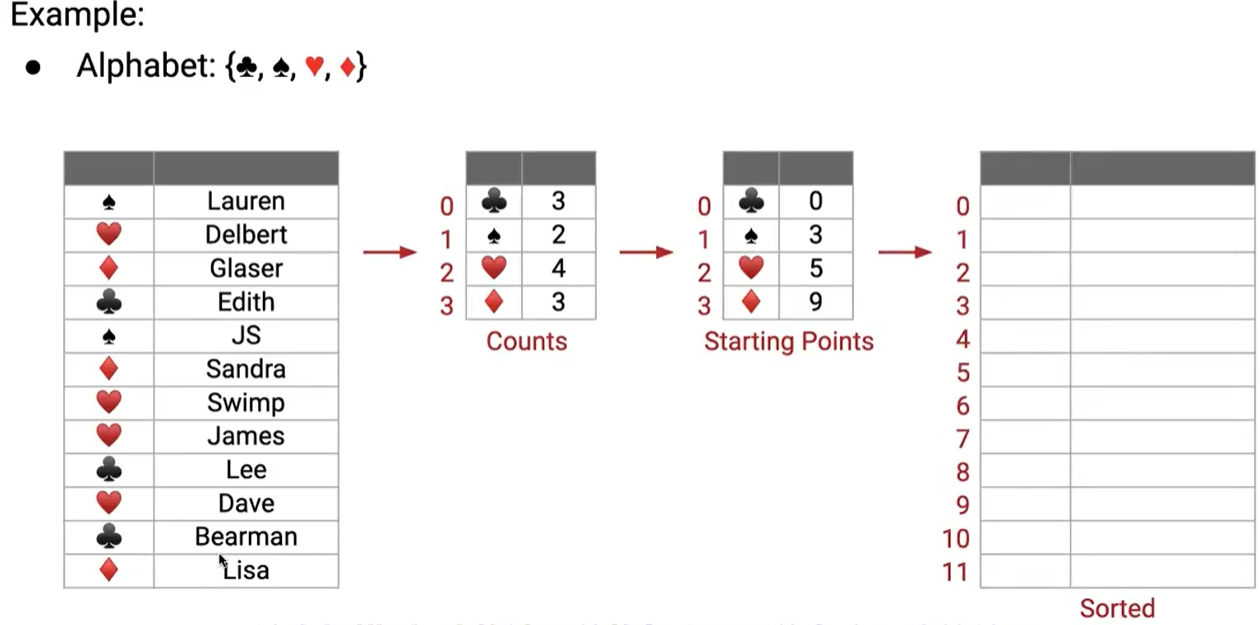
经过第一次扫描后,我可以根据counts表,得出这样一个 Starting Points 的元素索引表,来记录下一个对应的元素应该放置在哪个索引处,每次放置之后,更新索引表中的对应元素
计数排序 vs 快速排序
考虑城市人口排名的情形,城市人口是不连续的,如果在这里我们使用计数排序的话,需要列一个非常非常大的计数表

计数排序
实际上我需要两个变量来表示计数排序,一个用于告诉我元素的数量在增加,第二个变量告诉我,字母表的大小在增加
在花色分类中,字母表大小为4,而在城市人口排名中,字母表的大小为3700万
这样问题可以以两种不同方式增长
如果我们有 k 个不同的种类,而字母表大小为 R,那么时间复杂度为 θ(N+R)\theta(N+R)θ(N+R) ,空间使用情况仍然为 θ(N+R)\theta(N+R)θ(N+R)
(时间复杂度中的 R 来源于我在第一次遍历数组之后,还需要遍历 R 数组将对应的索引填进去)
基数排序
LSD
我们可以将每一个编号看作一个数字或者具有不同位数的元素
我们从最低有效位开始排序,然后逐步向最高有效位排序,同时每次排序保证是稳定的(也就是相同的数字,相对位置保持不变)
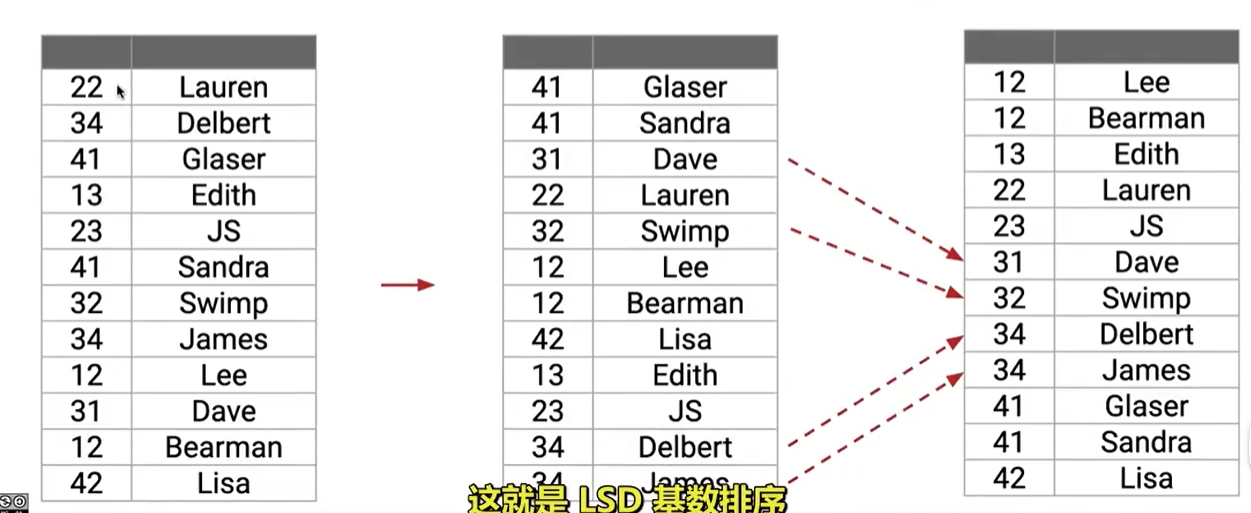
这样我们的时间复杂度为 θ(W(N+R))\theta(W(N+R))θ(W(N+R))
其中 N 表示元素的数量,R 表示字母表的大小,W 表示元素的宽度(位数)
相当于对每一位都进行一次计数排序
MSD
但是如果我的字符串非常长,那么 LSD 可能就会变得很慢,归并排序不会在较长的字符串上变慢,因为必须比较所有字符
我们可以从最高有效位开始比较
但是 MSD 会出现不稳定的情况
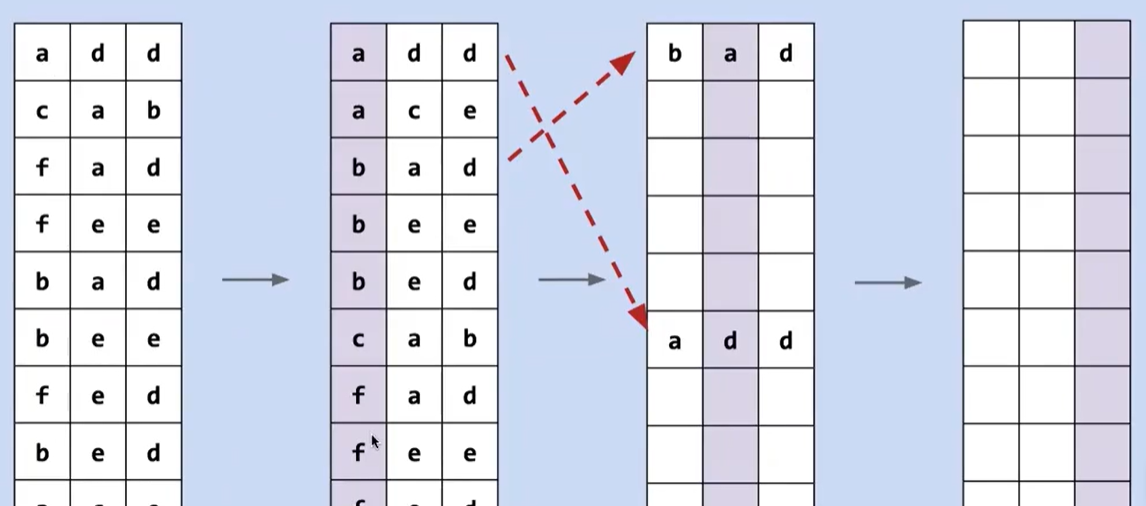
这样直接从最高位开始进行排序,会因为不稳定导致排序错误
为此,我们可以将其分解成子问题,比如一旦将所有以 a 开头的单词归类,下一步将是对这个子问题进行排序,而这些元素不会越界到 b 的范围
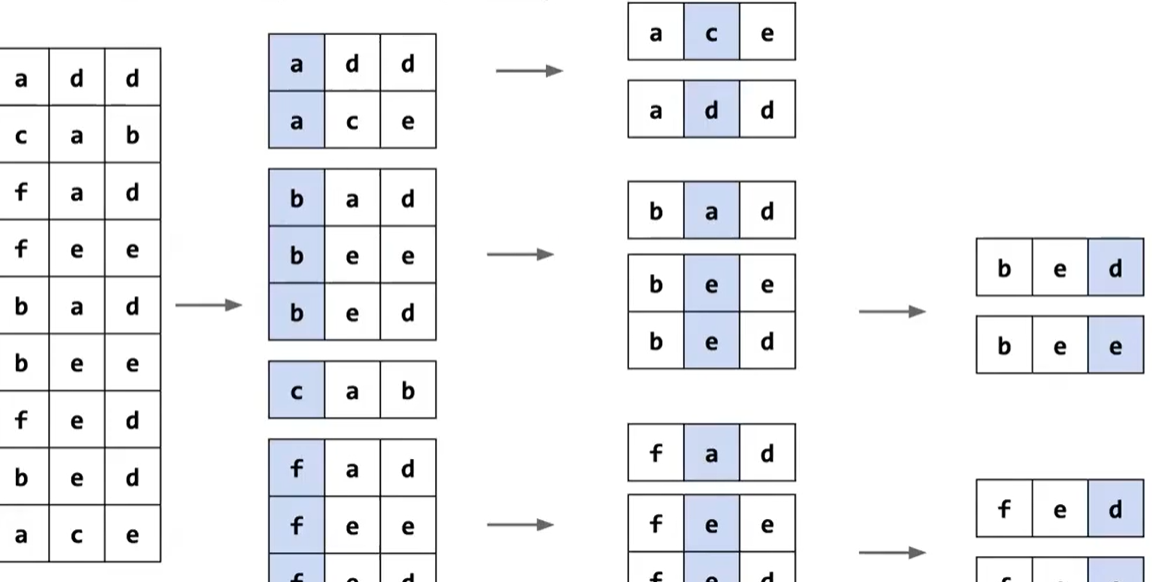
MSD 的时间复杂度有不同的情况
- 最好情况:比较最高位即完成,θ(N+R)\theta(N+R)θ(N+R)
- 最坏情况:需要比较每一位,退化成 LSD ,θ(WN+WR)\theta(WN+WR)θ(WN+WR)
LSD vs Merge Sort
实际情况;
- 我们认为字母表是常数,LSD 时间复杂度为 θ(WN)\theta(WN)θ(WN)
- 归并排序在 θ(NlogN)\theta(NlogN)θ(NlogN) 到 θ(WNlogN)\theta(WNlogN)θ(WNlogN) 之间
而具体来说哪一个更好呢?这取决于实际情况
- LSD 更快
- N非常非常大
- 比较的字符串之间非常相似
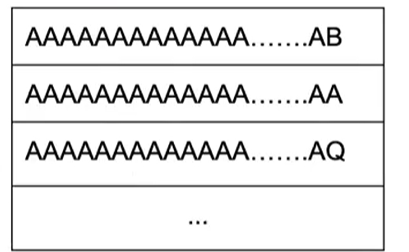
- 归并排序更快
- 比较的字符串之间差异非常大

