特性阻抗的近似计算
特性阻抗的近似计算:
设计一个指定的特性阻抗,实际上就是不断调整线宽、介质厚度和介电常数的过程。如果知道传输线的长度和导线周围材料的介电常数,计算出特性阻抗并运用上面的关系式,就可以计算出其他所有参数。
当然,不同类型的横截面,它的几何特征和特性阻抗的关系式也不同。从导线的横截面几何结构中求解特性阻抗,通常可以使用如下3种分析方法。
1.经验法则;
2.解析近似式;
3.二维场求解器。
对于FR4板上的微带线和带状线,有两个关于特性阻抗的最重要的经验法则。图7.30示例了50 Ω传输线的两种横截面。

图7.3050Ω传输线的两种不同比例的横截面。左图:50 Ω微带线,w=2h;右图:50Ω带状线,b=2W
提示: 由经验法则,FR4板上50 Ω微带线的线宽等于介质厚度的2倍。而50 Ω带状线的两平面之间的总介质厚度等于线宽的2倍。
只有3种类型的横截面有确切的公式,这3种横截面类型为同轴型、双圆杆型和圆杆一平平面型,如图7.31所示,其他的都只有近似公式。
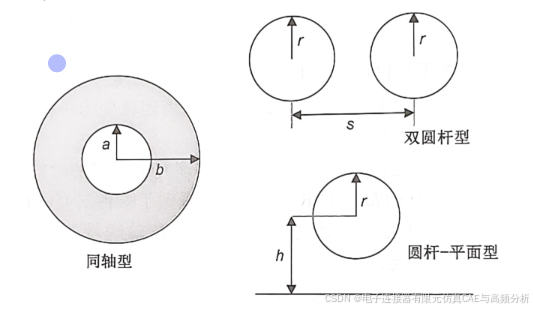
同轴型横截面的特性阻抗与横截面的关系式为:
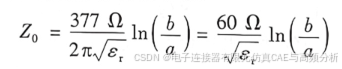
双圆杆型横截面的特性阻抗为:
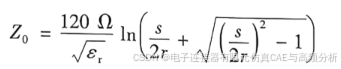
圆杆-平面型横截面的特性阻抗为:
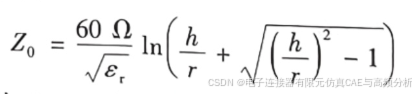
其中,表示特性阻抗(单位为Ω), a表示同轴线的内半径(单位为in),b表示同轴线的外半外半径(单位为in),r表示圆杆的半径(单位为in),s表示两圆杆的中心距(单位为in),h表示圆示圆杆中心到平面的距离(单位为in),
![]() 表示材料的介电常数。
表示材料的介电常数。
这些关系式假设电场空间全部均匀填充了介质材料。如果假设不成立,限制信号传播速度的有效介电常数与不同介电常数之间的关系比较复杂,就只能通过场求解器计算得出。
如果介质是均匀分布的,这些关系式就很准确,可以用于校准二维场求解器。
提示: 除了少数特殊情况,所有其他关于特性阻抗和几何结构的公式都是近似的。如果误差超过5%,就会造成设计周期和成本大幅增加,近似方法就不能用于传输线的设计签发(sign-off)。当要求考虑准确度时,应该使用经过验证的二维场求解器。
近似的作用在于指出了几何结构各参数之间的关系,可以用于电子表格中的灵敏度分析。对于微带线,IPC推荐的通用近似式为
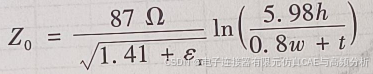
对于带状线,IPC推荐的通用近似式为
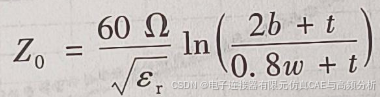
其中,表示特性阻抗(单位为Ω),h表示信号线与平面之间的介质厚度(单位为mil),w表示线宽(单位为mil),b表示平面之间的距离(单位为mil),t表示金属厚度(单位为mil),
![]() 表示介电常数。
表示介电常数。
如果忽略线条厚度t的影响,则这两种结构的特性阻抗仅与介质厚度和线宽的比值有关,这是一个非常重要的关系式。
提示: 在一阶模型中,微带线和带状线的特性阻抗与介质厚度和线宽的比值成比例变化。只要这个比值保持不变,特性阻抗就恒定不变。
例如,如果线宽和介质厚度都加倍,则一阶近似模型中的特性阻抗保持不变。
虽然这些方程看似复杂,但是它的准确度却无法度量。想要知道近似的准确度,唯一的方法是把近似值与使用经过验证的场求解器所得的结果相比较。
